內容提要
講完了優化的基本知識,我們來看一下g2o的結構。本篇將討論g2o的程式碼結構,並帶著大家一起寫一個簡單的雙檢視bundle adjustment:從兩張影象中估計相機運動和特徵點位置。你可以把它看成一個基於稀疏特徵點的單目VO。
g2o的結構
g2o全稱是什麼?來跟我大聲說一遍:General Graph Optimization!你可以叫它g土o,g二o,g方o,總之我也不知道該怎麼叫它……
所謂的通用圖優化。
為何叫通用呢?g2o的核裡帶有各種各樣的求解器,而它的頂點、邊的型別則多種多樣。通過自定義頂點和邊,事實上,只要一個優化問題能夠表達成圖,那麼就可以用g2o去求解它。常見的,比如bundle adjustment,ICP,資料擬合,都可以用g2o來做。甚至我還在想神經網路能不能寫成圖優化的形式呢……
從程式碼層面來說,g2o是一個c++編寫的專案,用cmake構建。它的github地址在:https://github.com/RainerKuemmerle/g2o
它是一個重度模板類的c++專案,其中矩陣資料結構多來自Eigen。首先我們來掃一眼它的目錄下面都有什麼吧:
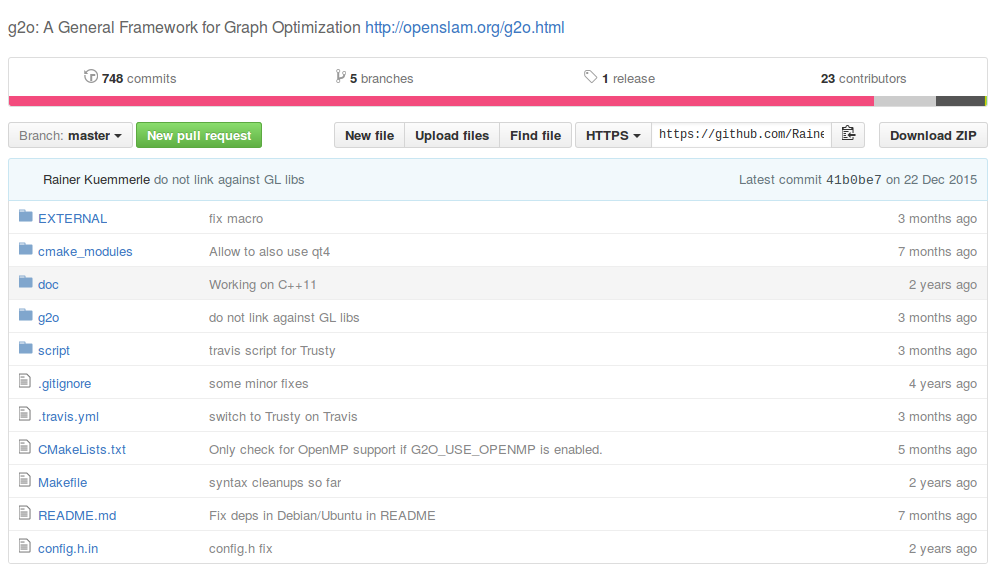
如你所見,g2o專案中含有若干資料夾。刨開那些gitignore之類的零碎檔案,主要有以下幾個:
- EXTERNAL 三方庫,有ceres, csparse, freeglut,可以選擇性地編譯;
- cmake_modules 給cmake用來尋找庫的檔案。我們用g2o時也會用它裡頭的東西,例如FindG2O.cmake
- doc 文件。包括g2o自帶的說明書(難度挺大的一個說明文件)。
- g2o 最重要的原始碼都在這裡!
- script 在android等其他系統編譯用的指令碼,由於我們在ubuntu下就沒必要多講了。
綜上所述,最重要的就是g2o的原始碼檔案啦!所以我們要進一步展開看一看!
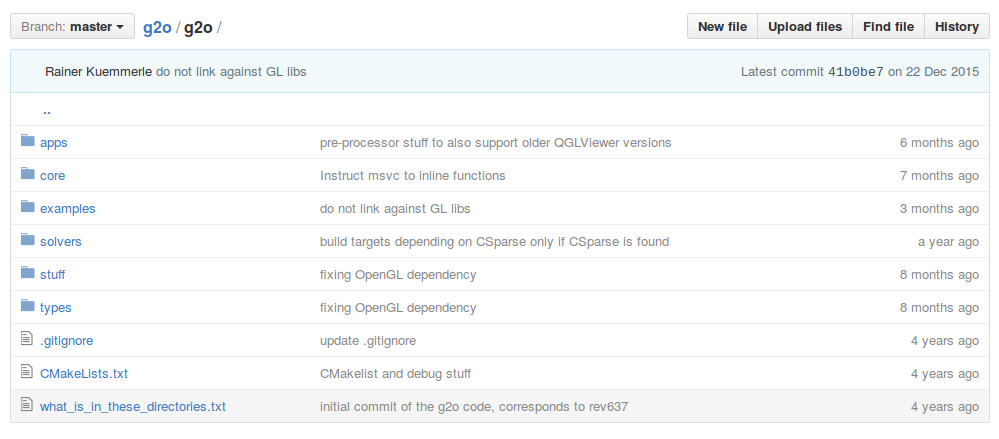
我們同樣地介紹一下各資料夾的內容:
- apps 一些應用程式。好用的g2o_viewer就在這裡。其他還有一些不常用的命令列工具等。
- core 核心元件,很重要!基本的頂點、邊、圖結構的定義,演算法的定義,求解器介面的定義在這裡。
- examples 一些例程,可以參照著這裡的東西來寫。不過註釋不太多。
- solvers 求解器的實現。主要來自choldmod, csparse。在使用g2o時要先選擇其中一種。
- stuff 對使用者來講可有可無的一些工具函式。
- types 各種頂點和邊,很重要!我們使用者在構建圖優化問題時,先要想好自己的頂點和邊是否已經提供了定義。如果沒有,要自己實現。如果有,就用g2o提供的即可。
就經驗而言,solvers給人的感覺是大同小異,而 types 的選取,則是 g2o 使用者主要關心的內容。然後 core 下面的內容,我們要爭取弄的比較熟悉,才能確保使用中出現錯誤可以正確地應對。
那麼,g2o最基本的類結構是怎麼樣的呢?我們如何來表達一個Graph,選擇求解器呢?我們祭出一張圖:
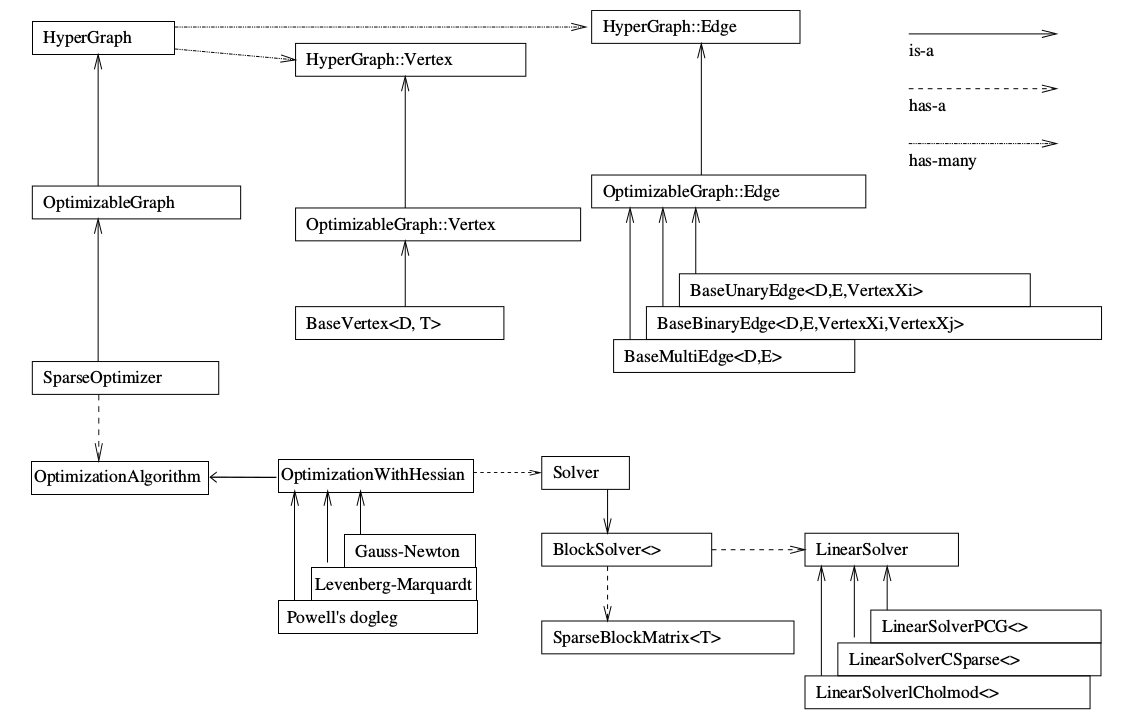
這個圖第一次看,可能覺得有些混亂。但是隨著g2o越用越多,你會發現越來越喜歡這個圖……現在請讀者跟著我的順序來看這個圖。
先看上半部分。SparseOptimizer 是我們最終要維護的東東。它是一個Optimizable Graph,從而也是一個Hyper Graph。一個 SparseOptimizer 含有很多個頂點 (都繼承自 Base Vertex)和很多個邊(繼承自 BaseUnaryEdge, BaseBinaryEdge或BaseMultiEdge)。這些 Base Vertex 和 Base Edge 都是抽象的基類,而實際用的頂點和邊,都是它們的派生類。我們用 SparseOptimizer.addVertex 和 SparseOptimizer.addEdge 向一個圖中新增頂點和邊,最後呼叫 SparseOptimizer.optimize 完成優化。
在優化之前,需要指定我們用的求解器和迭代演算法。從圖中下半部分可以看到,一個 SparseOptimizer 擁有一個 Optimization Algorithm,繼承自Gauss-Newton, Levernberg-Marquardt, Powell's dogleg 三者之一(我們常用的是GN或LM)。同時,這個 Optimization Algorithm 擁有一個Solver,它含有兩個部分。一個是 SparseBlockMatrix ,用於計算稀疏的雅可比和海塞; 一個是用於計算迭代過程中最關鍵的一步 $$H \Delta x = -b $$ 這就需要一個線性方程的求解器。而這個求解器,可以從 PCG, CSparse, Choldmod 三者選一。
綜上所述,在g2o中選擇優化方法一共需要三個步驟:
- 選擇一個線性方程求解器,從 PCG, CSparse, Choldmod中選,實際則來自 g2o/solvers 資料夾中定義的東東。
- 選擇一個 BlockSolver 。
- 選擇一個迭代策略,從GN, LM, Doglog中選。
這樣一來,讀者是否對g2o就更清楚的認識了呢?
小蘿蔔:師兄你慢點,我已經暈了……
雙檢視bundle adjustment:
既然小蘿蔔同學已經暈了,想必我們也成功地把讀者朋友都繞進去了。既繞之則繞之,下面我們來通過一個例項,更深入地理解 g2o 的用法。這個例項是什麼呢?我們來寫一個雙檢視的bundle adjustment吧!
程式碼的git地址:https://github.com/gaoxiang12/g2o_ba_example
首先,師兄還是拿出那兩張萬年不變的老圖:
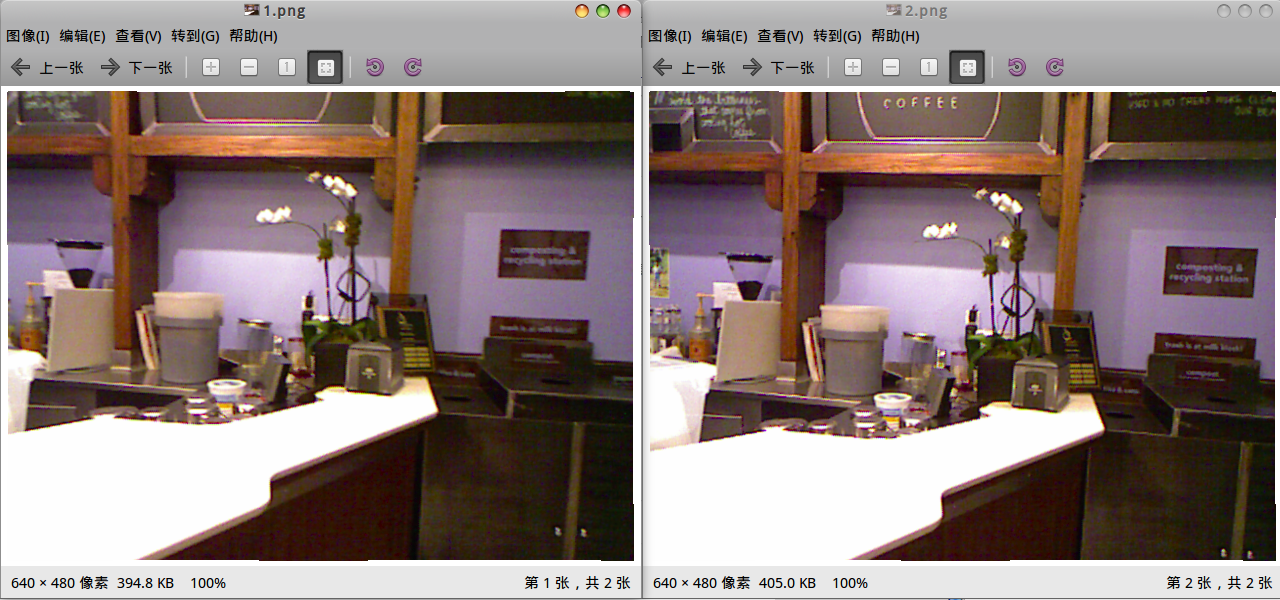
我們的目標是估計這兩個圖之間的運動。雖然我們在《一起做》裡講過這件事怎麼做了,但那是在RGBD的條件下。現在,我們沒有深度圖,只有這兩張影象和相機內參,請問如何估計相機的運動?
呃,這個問題好像還挺複雜的。我們需要用一點數學來描述它。所以請大家耐心看我推一會兒公式。
求解這個問題,當下有兩種思路。其一是通過特徵點來求,其二是直接通過畫素來求。第一種也叫做 sparse 方式,第二種叫做相對的 dense 方式。由於主流仍在用特徵點,所以我們例程也用特徵點。
特徵點方法的觀點是:一個影象可以用幾百個具有代表性的,比較穩定的點來表示。一旦我們有了這些點,就可以忽略圖中的其餘部分,而只關注這些點。(dense 思路則反對這一觀點,認為它丟棄了影象大部分資訊,畢竟一個640x480的圖有30萬個點,而特徵點只有幾百個)。
採用特徵點的思路,那麼問題變為:給定$N$個兩張圖中一一對應的點,記作:$${z_1} = \left\{ {z_1^1,z_1^2, \ldots ,z_1^N} \right\},{z_2} = \left\{ {z_2^1,z_2^2, \ldots ,z_2^N} \right\} $$ 以及相機內參矩陣 $C$,求解兩個圖中的相機運動$R,t$。
注:字元$z$的上標不是幾次方的意思,而是第幾個點。採用上標的原因是為了避免雙下標帶來的麻煩。同時,每個點的具體值$z$,是指該點對應的畫素座標:$z_i^j = [u,v]_i^j$,它們是二維的。
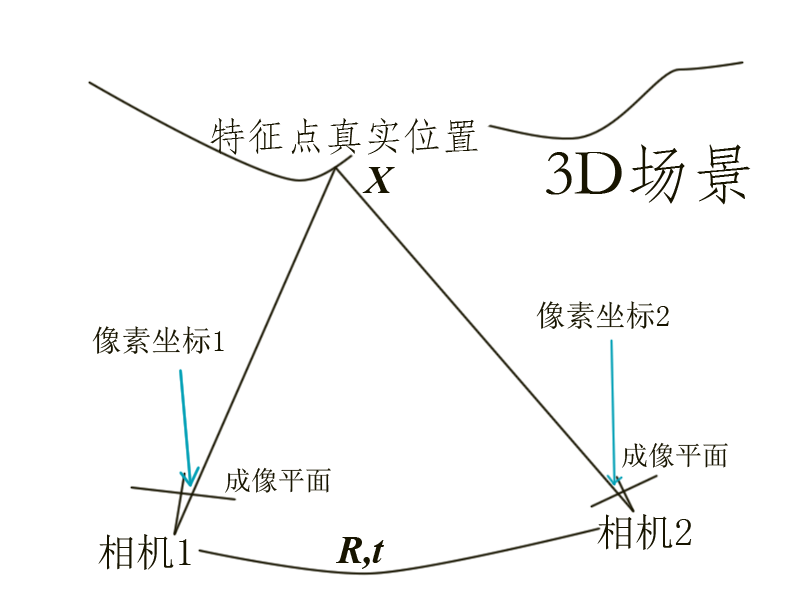
小蘿蔔:師兄啊,這圖一股濃濃的山寨味啊。
不管它,總之,假設相機1的位姿為單位矩陣,對於任意一個特徵點,它在三維空間的真實座標位於 $X^j$,而在兩個相機座標系上看來是 $z_1^j, z_2^j$。根據投影關係,我們有:
\[ \begin{equation} {\lambda _1}\left[ \begin{array}{l}
z_1^j\\
1
\end{array} \right] = C{X^j},\quad {\lambda _2}\left[ \begin{array}{l}
z_2^j\\
1
\end{array} \right] = C\left( {R{X^j} + t} \right) \end{equation}\]
這裡的 $\lambda_1, \lambda_2$ 表示兩個畫素的深度值,說白了也就是相機1座標下$X^j$的$z$座標。雖然我們不知道這個實際的$X^j$是什麼,但它和$z$之間的關係,是可以列寫出來的。
這個問題的傳統求解方式,是把兩個方程中的$X^j$消去,得到只關於$z, R, t$的關係式,然後進行優化。這條道路通向對極幾何和基礎矩陣(Essential Matrix),理論上,我們需要大於八個的匹配點就能計算出$R,t$。但這裡我們並不這樣做,因為我們是在介紹圖優化嘛。
在圖優化中,我們構建一個優化問題,並表示成圖去求解。這裡的優化問題是什麼呢?這可以這樣寫:
\[ \begin{equation} \mathop {\min }\limits_{{X^j},R,t} {\left\| {\frac{1}{{{\lambda _1}}}C{X^j} - {{\left[ {z_1^j,1} \right]}^T}} \right\|^2} + {\left\| {\frac{1}{{{\lambda _2}}}C\left( {R{X^j} + t} \right) - {{\left[ {z_2^j,1} \right]}^T}} \right\|^2} \end{equation} \]
由於各種噪聲的存在,投影關係不能完美滿足,所以我們轉而優化它們誤差的二範數。那麼對每一個特徵點,我們都能寫出這樣一個二範數的誤差項。對它們進行求和,就得到了整個優化問題:
\[ \begin{equation} \mathop {\min }\limits_{X,R,t} \sum\limits_{j = 1}^N {{{\left\| {\frac{1}{{{\lambda _1}}}C{X^j} - {{\left[ {z_1^j,1} \right]}^T}} \right\|}^2} + {{\left\| {\frac{1}{{{\lambda _2}}}C\left( {R{X^j} + t} \right) - {{\left[ {z_2^j,1} \right]}^T}} \right\|}^2}} \end{equation} \]
它叫做最小化重投影誤差問題(Minimization of Reprojection error)。當然,它很遺憾地,是個非線性,非凸的優化問題,這意味著我們不一定能求解它,也不一定能找到全域性最優的解。在實際操作中,我們實際上是在調整每個$X^j$,使得它們更符合每一次觀測$z^j$,也就是使每個誤差項都儘量的小。由於這個原因,它也叫做捆集調整(Bundle Adjustment)。
BA很容易表述成圖優化的形式。在這個雙檢視BA中,一種有兩種結點:
- 相機位姿結點:表達兩個相機所在的位置,是一個$SE(3)$裡的元素。
- 特徵點的空間位置結點:是一個XYZ座標。
相應的,邊主要表示空間點到畫素座標的投影關係。也就是
\[\lambda \left[ \begin{array}{l}
{z^j}\\
1
\end{array} \right] = C\left( {R{X^j} + t} \right)\] 這件事情嘍。
實現
下面我們來用g2o實現一下BA。選取的結點和邊如下:
- 結點1:相機位姿結點:g2o::VertexSE3Expmap,來自<g2o/types/sba/types_six_dof_expmap.h>;
- 結點2:特徵點空間座標結點:g2o::VertexSBAPointXYZ,來自<g2o/types/sba/types_sba.h>;
- 邊:重投影誤差:g2o::EdgeProjectXYZ2UV,來自<g2o/types/sba/types_six_dof_expmap.h>;
為了給讀者更深刻的印象,我們顯示一下邊的原始碼(也請讀者最好親自開啟g2o下這幾個檔案看一下頂點和邊的定義):
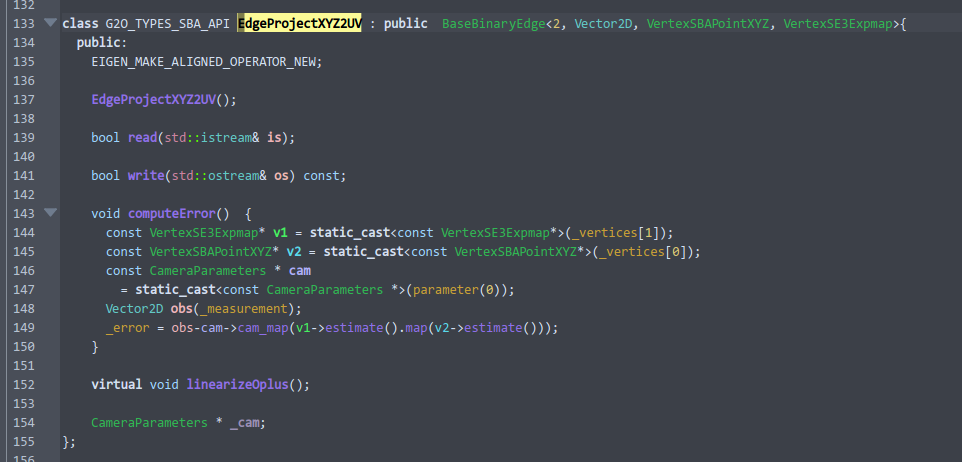
這個是 EdgeProjectXYZ2UV 邊的定義。它是一個Binary Edge,後面的模板參數列示,它的資料是2維的,來自Eigen::Vector2D,它連線的兩個頂點必須是 VertexSBAPointXYZ, VertexSE3Expmap。 我們還能看到它的 computeError 定義,和前面給出的公式是一致的。注意到計算Error時,它呼叫了 g2o::CameraParameters 作為引數,所以我們在設定這條邊時也需要給定一個相機引數。
鋪墊了那麼多之後,給出我們的原始碼:
1 /** 2 * BA Example 3 * Author: Xiang Gao 4 * Date: 2016.3 5 * Email: gaoxiang12@mails.tsinghua.edu.cn 6 * 7 * 在這個程式中,我們讀取兩張影象,進行特徵匹配。然後根據匹配得到的特徵,計算相機運動以及特徵點的位置。這是一個典型的Bundle Adjustment,我們用g2o進行優化。 8 */ 9 10 // for std 11 #include <iostream> 12 // for opencv 13 #include <opencv2/core/core.hpp> 14 #include <opencv2/highgui/highgui.hpp> 15 #include <opencv2/features2d/features2d.hpp> 16 #include <boost/concept_check.hpp> 17 // for g2o 18 #include <g2o/core/sparse_optimizer.h> 19 #include <g2o/core/block_solver.h> 20 #include <g2o/core/robust_kernel.h> 21 #include <g2o/core/robust_kernel_impl.h> 22 #include <g2o/core/optimization_algorithm_levenberg.h> 23 #include <g2o/solvers/cholmod/linear_solver_cholmod.h> 24 #include <g2o/types/slam3d/se3quat.h> 25 #include <g2o/types/sba/types_six_dof_expmap.h> 26 27 28 using namespace std; 29 30 // 尋找兩個影象中的對應點,畫素座標系 31 // 輸入:img1, img2 兩張影象 32 // 輸出:points1, points2, 兩組對應的2D點 33 int findCorrespondingPoints( const cv::Mat& img1, const cv::Mat& img2, vector<cv::Point2f>& points1, vector<cv::Point2f>& points2 ); 34 35 // 相機內參 36 double cx = 325.5; 37 double cy = 253.5; 38 double fx = 518.0; 39 double fy = 519.0; 40 41 int main( int argc, char** argv ) 42 { 43 // 呼叫格式:命令 [第一個圖] [第二個圖] 44 if (argc != 3) 45 { 46 cout<<"Usage: ba_example img1, img2"<<endl; 47 exit(1); 48 } 49 50 // 讀取影象 51 cv::Mat img1 = cv::imread( argv[1] ); 52 cv::Mat img2 = cv::imread( argv[2] ); 53 54 // 找到對應點 55 vector<cv::Point2f> pts1, pts2; 56 if ( findCorrespondingPoints( img1, img2, pts1, pts2 ) == false ) 57 { 58 cout<<"匹配點不夠!"<<endl; 59 return 0; 60 } 61 cout<<"找到了"<<pts1.size()<<"組對應特徵點。"<<endl; 62 // 構造g2o中的圖 63 // 先構造求解器 64 g2o::SparseOptimizer optimizer; 65 // 使用Cholmod中的線性方程求解器 66 g2o::BlockSolver_6_3::LinearSolverType* linearSolver = new g2o::LinearSolverCholmod<g2o::BlockSolver_6_3::PoseMatrixType> (); 67 // 6*3 的引數 68 g2o::BlockSolver_6_3* block_solver = new g2o::BlockSolver_6_3( linearSolver ); 69 // L-M 下降 70 g2o::OptimizationAlgorithmLevenberg* algorithm = new g2o::OptimizationAlgorithmLevenberg( block_solver ); 71 72 optimizer.setAlgorithm( algorithm ); 73 optimizer.setVerbose( false ); 74 75 // 新增節點 76 // 兩個位姿節點 77 for ( int i=0; i<2; i++ ) 78 { 79 g2o::VertexSE3Expmap* v = new g2o::VertexSE3Expmap(); 80 v->setId(i); 81 if ( i == 0) 82 v->setFixed( true ); // 第一個點固定為零 83 // 預設值為單位Pose,因為我們不知道任何資訊 84 v->setEstimate( g2o::SE3Quat() ); 85 optimizer.addVertex( v ); 86 } 87 // 很多個特徵點的節點 88 // 以第一幀為準 89 for ( size_t i=0; i<pts1.size(); i++ ) 90 { 91 g2o::VertexSBAPointXYZ* v = new g2o::VertexSBAPointXYZ(); 92 v->setId( 2 + i ); 93 // 由於深度不知道,只能把深度設定為1了 94 double z = 1; 95 double x = ( pts1[i].x - cx ) * z / fx; 96 double y = ( pts1[i].y - cy ) * z / fy; 97 v->setMarginalized(true); 98 v->setEstimate( Eigen::Vector3d(x,y,z) ); 99 optimizer.addVertex( v ); 100 } 101 102 // 準備相機引數 103 g2o::CameraParameters* camera = new g2o::CameraParameters( fx, Eigen::Vector2d(cx, cy), 0 ); 104 camera->setId(0); 105 optimizer.addParameter( camera ); 106 107 // 準備邊 108 // 第一幀 109 vector<g2o::EdgeProjectXYZ2UV*> edges; 110 for ( size_t i=0; i<pts1.size(); i++ ) 111 { 112 g2o::EdgeProjectXYZ2UV* edge = new g2o::EdgeProjectXYZ2UV(); 113 edge->setVertex( 0, dynamic_cast<g2o::VertexSBAPointXYZ*> (optimizer.vertex(i+2)) ); 114 edge->setVertex( 1, dynamic_cast<g2o::VertexSE3Expmap*> (optimizer.vertex(0)) ); 115 edge->setMeasurement( Eigen::Vector2d(pts1[i].x, pts1[i].y ) ); 116 edge->setInformation( Eigen::Matrix2d::Identity() ); 117 edge->setParameterId(0, 0); 118 // 核函式 119 edge->setRobustKernel( new g2o::RobustKernelHuber() ); 120 optimizer.addEdge( edge ); 121 edges.push_back(edge); 122 } 123 // 第二幀 124 for ( size_t i=0; i<pts2.size(); i++ ) 125 { 126 g2o::EdgeProjectXYZ2UV* edge = new g2o::EdgeProjectXYZ2UV(); 127 edge->setVertex( 0, dynamic_cast<g2o::VertexSBAPointXYZ*> (optimizer.vertex(i+2)) ); 128 edge->setVertex( 1, dynamic_cast<g2o::VertexSE3Expmap*> (optimizer.vertex(1)) ); 129 edge->setMeasurement( Eigen::Vector2d(pts2[i].x, pts2[i].y ) ); 130 edge->setInformation( Eigen::Matrix2d::Identity() ); 131 edge->setParameterId(0,0); 132 // 核函式 133 edge->setRobustKernel( new g2o::RobustKernelHuber() ); 134 optimizer.addEdge( edge ); 135 edges.push_back(edge); 136 } 137 138 cout<<"開始優化"<<endl; 139 optimizer.setVerbose(true); 140 optimizer.initializeOptimization(); 141 optimizer.optimize(10); 142 cout<<"優化完畢"<<endl; 143 144 //我們比較關心兩幀之間的變換矩陣 145 g2o::VertexSE3Expmap* v = dynamic_cast<g2o::VertexSE3Expmap*>( optimizer.vertex(1) ); 146 Eigen::Isometry3d pose = v->estimate(); 147 cout<<"Pose="<<endl<<pose.matrix()<<endl; 148 149 // 以及所有特徵點的位置 150 for ( size_t i=0; i<pts1.size(); i++ ) 151 { 152 g2o::VertexSBAPointXYZ* v = dynamic_cast<g2o::VertexSBAPointXYZ*> (optimizer.vertex(i+2)); 153 cout<<"vertex id "<<i+2<<", pos = "; 154 Eigen::Vector3d pos = v->estimate(); 155 cout<<pos(0)<<","<<pos(1)<<","<<pos(2)<<endl; 156 } 157 158 // 估計inlier的個數 159 int inliers = 0; 160 for ( auto e:edges ) 161 { 162 e->computeError(); 163 // chi2 就是 error*\Omega*error, 如果這個數很大,說明此邊的值與其他邊很不相符 164 if ( e->chi2() > 1 ) 165 { 166 cout<<"error = "<<e->chi2()<<endl; 167 } 168 else 169 { 170 inliers++; 171 } 172 } 173 174 cout<<"inliers in total points: "<<inliers<<"/"<<pts1.size()+pts2.size()<<endl; 175 optimizer.save("ba.g2o"); 176 return 0; 177 } 178 179 180 int findCorrespondingPoints( const cv::Mat& img1, const cv::Mat& img2, vector<cv::Point2f>& points1, vector<cv::Point2f>& points2 ) 181 { 182 cv::ORB orb; 183 vector<cv::KeyPoint> kp1, kp2; 184 cv::Mat desp1, desp2; 185 orb( img1, cv::Mat(), kp1, desp1 ); 186 orb( img2, cv::Mat(), kp2, desp2 ); 187 cout<<"分別找到了"<<kp1.size()<<"和"<<kp2.size()<<"個特徵點"<<endl; 188 189 cv::Ptr<cv::DescriptorMatcher> matcher = cv::DescriptorMatcher::create( "BruteForce-Hamming"); 190 191 double knn_match_ratio=0.8; 192 vector< vector<cv::DMatch> > matches_knn; 193 matcher->knnMatch( desp1, desp2, matches_knn, 2 ); 194 vector< cv::DMatch > matches; 195 for ( size_t i=0; i<matches_knn.size(); i++ ) 196 { 197 if (matches_knn[i][0].distance < knn_match_ratio * matches_knn[i][1].distance ) 198 matches.push_back( matches_knn[i][0] ); 199 } 200 201 if (matches.size() <= 20) //匹配點太少 202 return false; 203 204 for ( auto m:matches ) 205 { 206 points1.push_back( kp1[m.queryIdx].pt ); 207 points2.push_back( kp2[m.trainIdx].pt ); 208 } 209 210 return true; 211 }
在這個程式中,我們從命令列引數讀取兩個影象所在的位置,然後構建一個圖估計影象間運動和特徵點的空間位置。
整個工程的編譯方式使用cmake,請參考 github 工程進行編譯,這裡就不詳細說明了。(因為肯定又要提一堆Cmake方面的事情。)
編譯完成後,可以執行此程式,結果如下:
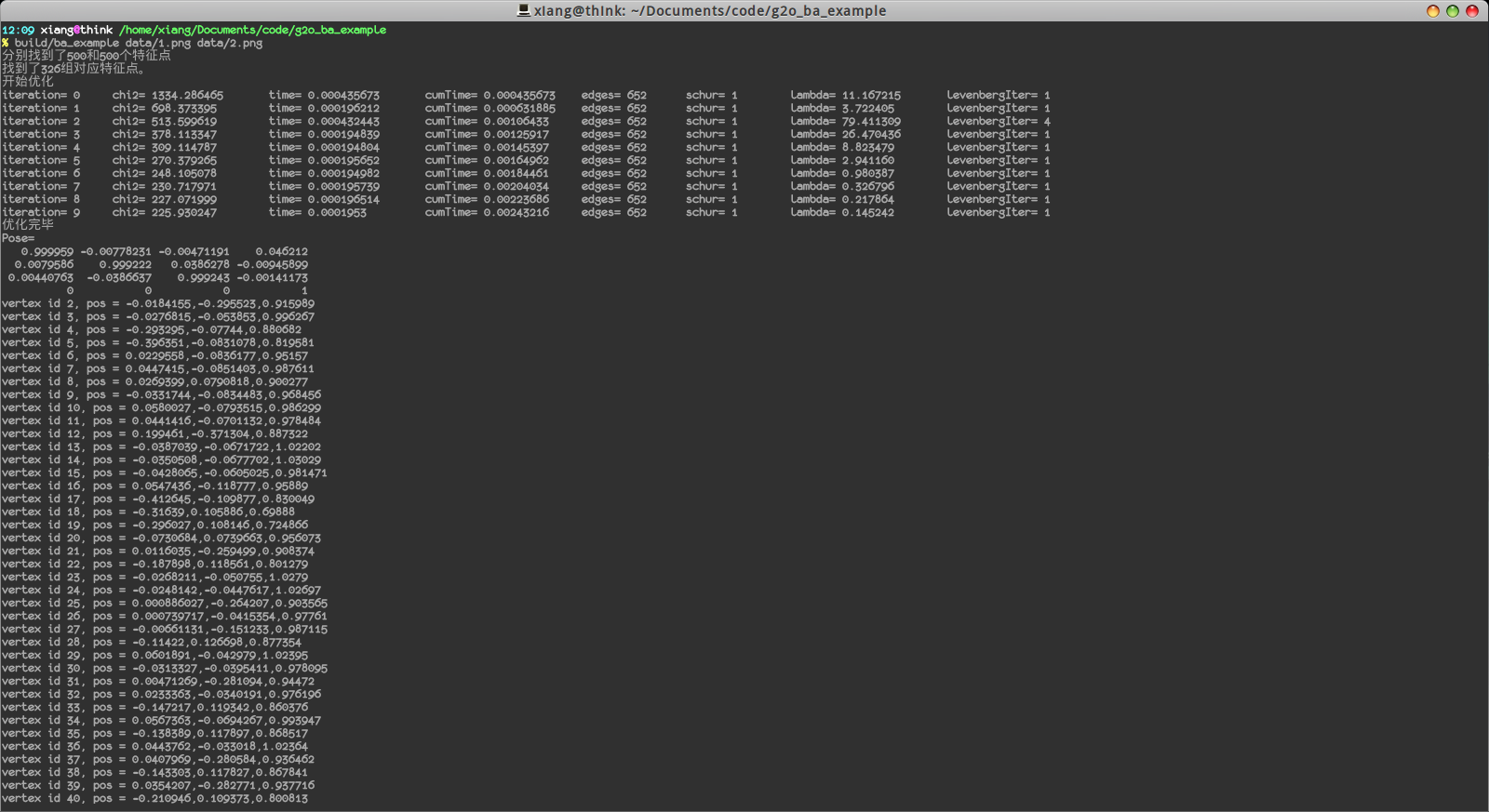
我們顯示了特徵點的數量,估計的位姿變換,以及各特徵點的空間位置。最後,還顯示了inliers的數量(我們把誤差太大的邊認為是outlier):
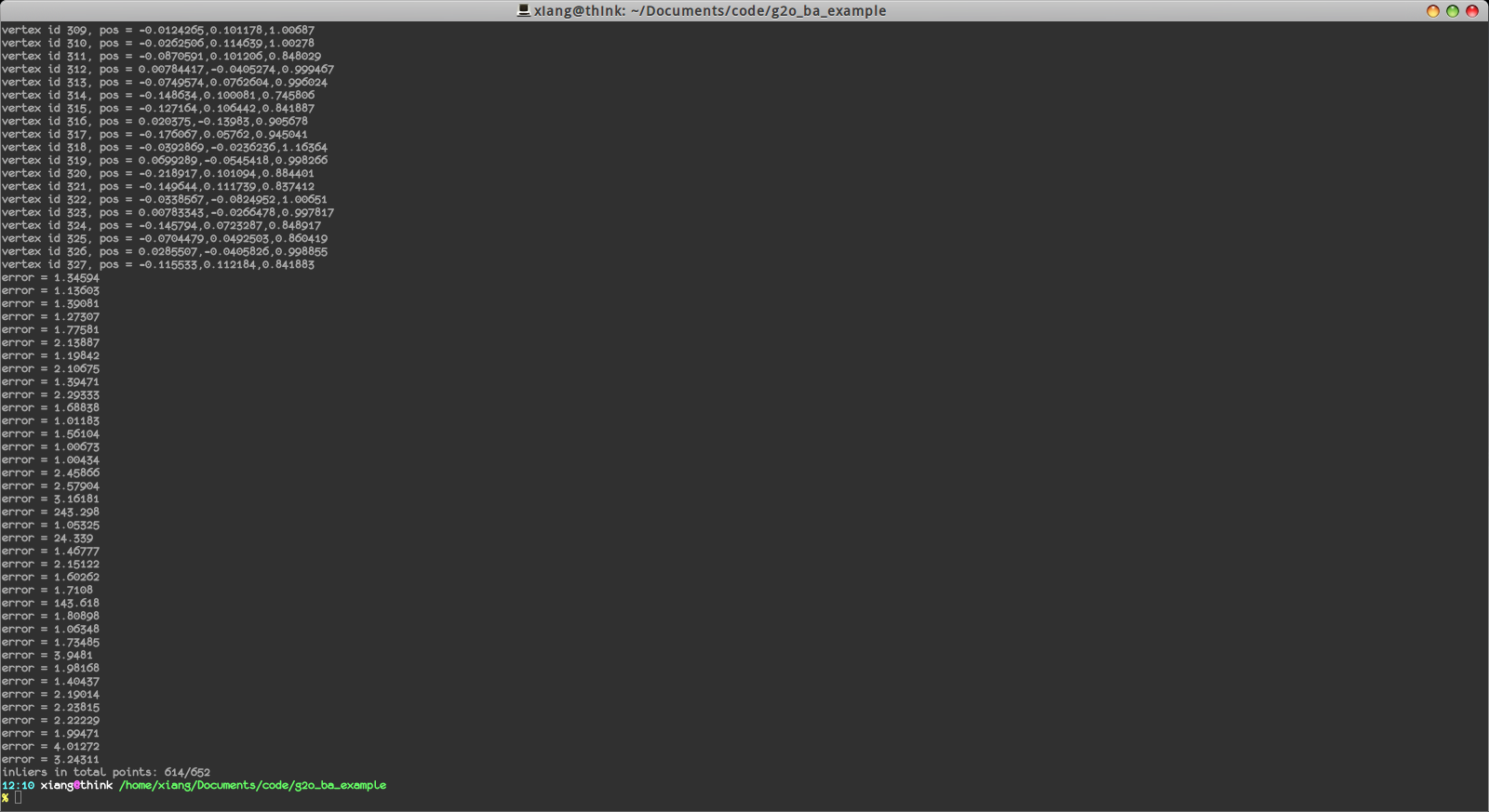
在652條邊中有614條邊是inlier,說明匹配還是挺正確的。
討論
關於單目BA還有一點要說,就是 scale 不確定性。由於投影公式中的$\lambda$存在,我們只能推得一個相對的深度,而無法確切的知道特徵點離我們有多少距離。如果我們把所有特徵點的座標放大一倍,把平移量$t$也乘以二,得到的結果是完全一樣的。
比方說:看奧特曼時,我們並不知道這其實是人類演員在模型裡打架。這就是單目帶來的尺度不確定性。
小蘿蔔:師兄你現在才知道嗎?我小時候就知道了啊!
小結
本節介紹了g2o的大致框架,並提供了一個計算單目雙檢視Bundle Adjustment的例程供讀者練習。
如果你覺得我的部落格有幫助,可以進行幾塊錢的小額贊助,幫助我把部落格寫得更好。