前言
本節我們將深入介紹視覺slam中的主流優化方法——圖優化(graph-based optimization)。下一節中,介紹一下非常流行的圖優化庫:g2o。
關於g2o,我13年寫過一個文件,然而隨著自己理解的加深,越發感覺不滿意。本著對讀者更負責任的精神,本文給大家重新講一遍圖優化和g2o。除了這篇文件,讀者還可以找到一篇關於圖優化的部落格: http://blog.csdn.net/heyijia0327 那篇文章有作者介紹的一個簡單案例,而本文則更注重對圖優化和g2o的理解與評註。
本節主要介紹圖優化的數學理論,下節再講g2o的組成方式及使用方法。
預備知識:優化
圖優化本質上是一個優化問題,所以我們先來看優化問題是什麼。
優化問題有三個最重要的因素:目標函式、優化變數、優化約束。一個簡單的優化問題可以描述如下:\[ \begin{equation} \min\limits_{x} F(x) \end{equation}\] 其中$x$為優化變數,而$F(x)$為優化函式。此問題稱為無約束優化問題,因為我們沒有給出任何約束形式。由於slam中優化問題多為無約束優化,所以我們著重介紹無約束的形式。
當$F(x)$有一些特殊性質時,對應的優化問題也可以用一些特殊的解法。例如,$F(x)$為一個線性函式時,則為線性優化問題(不過線性優化問題通常在有約束情形下討論)。反之則為非線性優化。對於無約束的非線性優化,如果我們知道它梯度的解析形式,就能直接求那些梯度為零的點,來解決這個優化:
\[\begin{equation} \frac{{dF}}{{dx}} = 0 \end{equation}\]
梯度為零的地方可能是函式的極大值、極小值或者鞍點。由於現在$F(x)$的形式不確定,我們只好遍歷所有的極值點,找到最小的作為最優解。
但是我們為什麼不這樣用呢?因為很多時候$F(x)$的形式太複雜,導致我們沒法寫出導數的解析形式,或者難以求解導數為零的方程。因此,多數時候我們使用迭代方式求解。從一個初值$x_0$出發,不斷地導致當前值附近的,能使目標函式下降的方式(反向梯度),然後沿著梯度方向走出一步,從而使得函式值下降一點。這樣反覆迭代,理論上對於任何函式,都能找到一個極小值點。
迭代的策略主要體現在如何選擇下降方向,以及如何選擇步長兩個方面。主要有 Gauss-Newton (GN)法和 Levenberg-Marquardt (LM)法兩種,它們的細節可以在維基上找到,我們不細說。請理解它們主要在迭代策略上有所不同,但是尋找梯度並迭代則是一樣的。
圖優化
所謂的圖優化,就是把一個常規的優化問題,以圖(Graph)的形式來表述。
圖是什麼呢?
圖是由頂點(Vertex)和邊(Edge)組成的結構,而圖論則是研究圖的理論。我們記一個圖為$G=\{ V, E \}$,其中$V$為頂點集,$E$為邊集。
頂點沒什麼可說的,想象成普通的點即可。
邊是什麼呢?一條邊連線著若干個頂點,表示頂點之間的一種關係。邊可以是有向的或是無向的,對應的圖稱為有向圖或無向圖。邊也可以連線一個頂點(Unary Edge,一元邊)、兩個頂點(Binary Edge,二元邊)或多個頂點(Hyper Edge,多元邊)。最常見的邊連線兩個頂點。當一個圖中存在連線兩個以上頂點的邊時,稱這個圖為超圖(Hyper Graph)。而SLAM問題就可以表示成一個超圖(在不引起歧義的情況下,後文直接以圖指代超圖)。
怎麼把SLAM問題表示成圖呢?
SLAM的核心是根據已有的觀測資料,計算機器人的運動軌跡和地圖。假設在時刻$k$,機器人在位置$x_k$處,用感測器進行了一次觀測,得到了資料$z_k$。感測器的觀測方程為:
\[ \begin{equation}{z_k} = h\left( {{x_k}} \right) \end{equation} \]
由於誤差的存在,$z_k$不可能精確地等於$h(x_k)$,於是就有了誤差:
\[ \begin{equation} {e_k} = {z_k} - h\left( {{x_k}} \right) \end{equation} \]
那麼,如果我們以$x_k$為優化變數,以$ \min\limits_x F_k (x_k) = \| e_k \| $為目標函式,就可以求得$x_k$的估計值,進而得到我們想要的東西了。這實際上就是用優化來求解SLAM的思路。
你說的優化變數$x_k$,觀測方程$z_k = h (x_k)$等等,它們具體是什麼東西呢?
這個取決於我們的引數化(parameterazation)。$x$可以是一個機器人的Pose(6自由度下為 $4\times 4$的變換矩陣$\mathbf{T}$ 或者 3自由度下的位置與轉角$[x,y,\theta]$,也可以是一個空間點(三維空間的$[x,y,z]$或二維空間的$[x,y]$)。相應的,觀測方程也有很多形式,如:
- 機器人兩個Pose之間的變換;
- 機器人在某個Pose處用鐳射測量到了某個空間點,得到了它離自己的距離與角度;
- 機器人在某個Pose處用相機觀測到了某個空間點,得到了它的畫素座標;
同樣,它們的具體形式很多樣化,這允許我們在討論slam問題時,不侷限於某種特定的感測器或姿態表達方式。
我明白優化是什麼意思了,但是它們怎麼表達成圖呢?
在圖中,以頂點表示優化變數,以邊表示觀測方程。由於邊可以連線一個或多個頂點,所以我們把它的形式寫成更廣義的 $z_k = h(x_{k1}, x_{k2}, \ldots )$,以表示不限制頂點數量的意思。對於剛才提到的三種觀測方程,頂點和邊是什麼形式呢?
- 機器人兩個Pose之間的變換;——一條Binary Edge(二元邊),頂點為兩個pose,邊的方程為${T_1} = \Delta T \cdot {T_2}$。
- 機器人在某個Pose處用鐳射測量到了某個空間點,得到了它離自己的距離與角度;——Binary Edge,頂點為一個2D Pose:$[x,y,\theta]^T$和一個Point:$[\lambda_x, \lambda_y]^T$,觀測資料是距離$r$和角度$b$,那麼觀測方程為:
\[ \begin{equation}
\left[
{\begin{array}{*{20}{c}}
{r}\\
{b}
\end{array}}
\right] = \left[ {
\begin{array}{*{20}{c}}
{\sqrt {{{({\lambda _x} - x)}^2} + {{({\lambda _y} - y)}^2}}}\\
{{{\tan }^{ - 1}}\left( {\frac{{{\lambda _y} - y}}{{{\lambda _x} - x}}} \right) - \theta }
\end{array}}
\right]
\end{equation}\] - 機器人在某個Pose處用相機觀測到了某個空間點,得到了它的畫素座標;——Binary Edge,頂點為一個3D Pose:$T$和一個空間點$\mathbf{x} = [x,y,z]^T$,觀測資料為畫素座標$z=[u,v]^T$。那麼觀測方程為:\[ \begin{equation} z = C ( R \mathbf{x} + t ) \end{equation} \]
$C$為相機內參,$R,t$為旋轉和平移。
舉這些例子,是為了讓讀者更好地理解頂點和邊是什麼東西。由於機器人可能使用各種感測器,故我們不限制頂點和邊的引數化之後的樣子。比如我(喪心病狂地在小蘿蔔身上)既加了鐳射,也用相機,還用了IMU,輪式編碼器,超聲波等各種感測器來做slam。為了求解整個問題,我的圖中就會有各種各樣的頂點和邊。但是不管如何,都是可以用圖來優化的。

(暗黑小蘿蔔 小眼神degined by Orchid Zhang)以後找不到工作我就去當插畫算了……
圖優化怎麼做
現在讓我們來仔細看一看圖優化是怎麼做的。假設一個帶有$n$條邊的圖,其目標函式可以寫成:
\[ \begin{equation} \min\limits_{x} \sum\limits_{k = 1}^n {{e_k}{{\left( {{x_k},{z_k}} \right)}^T}{\Omega _k}{e_k}\left( {{x_k},{z_k}} \right)} \end{equation}\]
關於這個目標函式,我們有幾句話要講。這些話都是很重要的,請讀者仔細去理解。
- $e$ 函式在原理上表示一個誤差,是一個向量,作為優化變數$x_k$和$z_k$符合程度的一個度量。它越大表示$x_k$越不符合$z_k$。但是,由於目標函式必須是標量,所以必須用它的平方形式來表達目標函式。最簡單的形式是直接做成平方:$e(x,z)^T e(x,z)$。進一步,為了表示我們對誤差各分量重視程度的不一樣,還使用一個資訊矩陣 $\Omega$ 來表示各分量的不一致性。
- 資訊矩陣 $\Omega$ 是協方差矩陣的逆,是一個對稱矩陣。它的每個元素$ \Omega_{i,j}$作為$e_i e_j$的係數,可以看成我們對$e_i, e_j$這個誤差項相關性的一個預計。最簡單的是把$\Omega$設成對角矩陣,對角陣元素的大小表明我們對此項誤差的重視程度。
- 這裡的$x_k$可以指一個頂點、兩個頂點或多個頂點,取決於邊的實際型別。所以,更嚴謹的方式是把它寫成$e_k ( z_k, x_{k1}, x_{k2}, \ldots )$,但是那樣寫法實在是太繁瑣,我們就簡單地寫成現在的樣子。由於$z_k$是已知的,為了數學上的簡潔,我們再把它寫成$e_k(x_k)$的形式。
於是總體優化問題變為$n$條邊加和的形式:
\[ \begin{equation} \min F(x) = \sum\limits_{k = 1}^n {{e_k}{{\left( {{x_k}} \right)}^T}{\Omega _k}{e_k}\left( {{x_k}} \right)} \end{equation}\]
重複一遍,邊的具體形式有很多種,可以是一元邊、二元邊或多元邊,它們的數學表達形式取決於感測器或你想要描述的東西。例如視覺SLAM中,在一個相機Pose $T_k$ 處對空間點$\mathbf{x}_k$進行了一次觀測,得到$z_k$,那麼這條二元邊的數學形式即為$${e_k}\left( {{x_k},{T_k},{z_k}} \right) = {\left( {{z_k} - C\left( {R{x_k} + t} \right)} \right)^T}{\Omega _k}\left( {{z_k} - C\left( {R{x_k} - t} \right)} \right)$$ 單個邊其實並不複雜。
現在,我們有了一個很多個節點和邊的圖,構成了一個龐大的優化問題。我們並不想展開它的數學形式,只關心它的優化解。那麼,為了求解優化,需要知道兩樣東西:一個初始點和一個迭代方向。為了數學上的方便,先考慮第$k$條邊$e_k(x_k)$吧。
我們假設它的初始點為${{\widetilde x}_k}$,並且給它一個$\Delta x$的增量,那麼邊的估計值就變為$F_k ( {\widetilde x}_k + \Delta x )$,而誤差值則從 $e_k(\widetilde x)$ 變為 $e_k({\widetilde x}_k + \Delta x )$。首先對誤差項進行一階展開:
\[ \begin{equation} {e_k}\left( {{{\widetilde x}_k} + \Delta x} \right) \approx {e_k}\left( {{{\widetilde x}_k}} \right) + \frac{{d{e_k}}}{{d{x_k}}}\Delta x = {e_k} + {J_k}\Delta x\end{equation} \]
這是的$J_k$是$e_k$關於$x_k$的導數,矩陣形式下為雅可比陣。我們在估計點附近作了一次線性假設,認為函式值是能夠用一階導數來逼近的,當然這在$\Delta x$很大時候就不成立了。
於是,對於第$k$條邊的目標函式項,有:
進一步展開:
$$\begin{array}{lll}{F_k}\left( {{{\widetilde x}_k} + \Delta x} \right) &=& {e_k}{\left( {{{\widetilde x}_k} + \Delta x} \right)^T}{\Omega _k}{e_k}\left( {{{\widetilde x}_k} + \Delta x} \right)\\
& \approx & {\left( {{e_k} + {J_k}\Delta x} \right)^T}{\Omega _k}\left( {{e_k} + J\Delta x} \right)\\
&=& e_k^T{\Omega _k}{e_k} + 2e_k^T{\Omega _k}{J_k}\Delta x + \Delta {x^T}J_k^T{\Omega _k}{J_k}\Delta x\\ &=& {C_k} + 2{b_k}\Delta x + \Delta {x^T}{H_k}\Delta x
\end{array}$$
在熟練的同學看來,這個推導就像$(a+b)^2=a^2+2ab+b^2$一樣簡單(事實上就是好吧)。最後一個式子是個定義整理式,我們把和$\Delta x$無關的整理成常數項 $C_k$ ,把一次項係數寫成 $2b_k$ ,二次項則為 $H_k$(注意到二次項係數其實是Hessian矩陣)。
請注意 $C_k$ 實際就是該邊變化前的取值。所以在$x_k$發生增量後,目標函式$F_k$項改變的值即為$$\Delta F_k = 2b_k \Delta x + \Delta x^T H_k \Delta x. $$
我們的目標是找到$\Delta x$,使得這個增量變為極小值。所以直接令它對於$\Delta x$的導數為零,有:
\[ \begin{equation} \frac{{d{F_k}}}{{d\Delta x}} = 2b + 2{H_k}\Delta x = 0 \Rightarrow {H_k}\Delta x = - b_k \end{equation} \]
所以歸根結底,我們求解一個線性方程組:\[ \begin{equation} H_k \Delta x = -b_k \end{equation} \]
如果把所有邊放到一起考慮進去,那就可以去掉下標,直接說我們要求解$$ H \Delta x = -b. $$
原來算了半天它只是個線性的!線性的誰不會解啊!
讀者當然會有這種感覺,因為線性規劃是規劃中最為簡單的,連小學生都會解這麼簡單的問題,為何21世紀前SLAM不這樣做呢?——這是因為在每一步迭代中,我們都要求解一個雅可比和一個海塞。而一個圖中經常有成千上萬條邊,幾十萬個待估計引數,這在以前被認為是無法實時求解的。
那為何後來又可以實時求解了呢?
SLAM研究者逐漸認識到,SLAM構建的圖,並非是全連通圖,它往往是很稀疏的。例如一個地圖裡大部分路標點,只會在很少的時刻被機器人看見,從而建立起一些邊。大多數時候它們是看不見的(就像後宮怨女一樣)。體現在數學公式中,雖然總體目標函式$F(x)$有很多項,但某個頂點$x_k$就只會出現在和它有關的邊裡面!
這會導致什麼?這導致許多和$x_k$無關的邊,比如說$e_j$,對應的雅可比$J_j$就直接是個零矩陣!而總體的雅可比$J$中,和$x_k$有關的那一列大部分為零,只有少數的地方,也就是和$x_k$頂點相連的邊,出現了非零值。
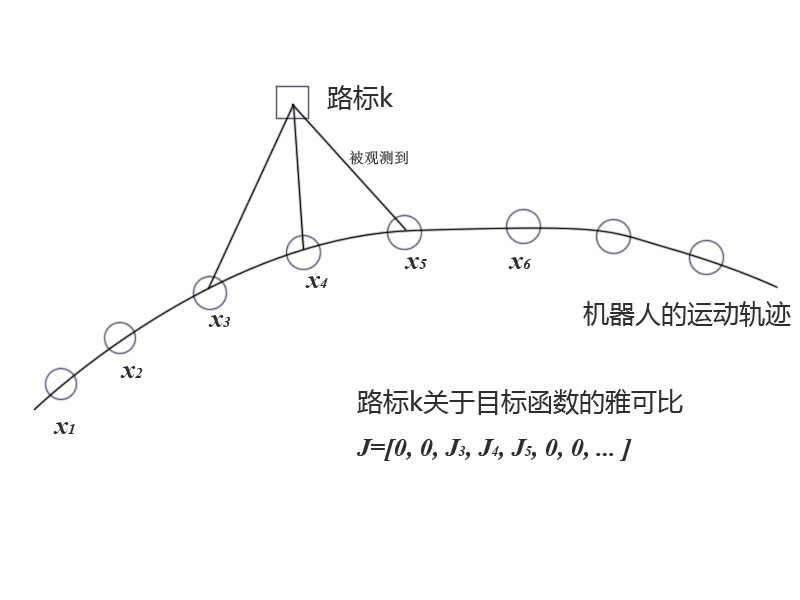
相應的二階導矩陣$H$中,大部分也是零元素。這種稀疏效能很好地幫助我們快速求解上面的線性方程。出於篇幅我們先不細說這是如何做到的了。稀疏代數庫包括SBA、PCG、CSparse、Cholmod等等。g2o正是使用它們來求解圖優化問題的。
要補充一點的是,在數值計算中,我們可以給出雅可比和海塞的解析形式進行計算,也可以讓計算機去數值計算這兩個陣,而我們只需要給出誤差的定義方式即可。
流形
等一下老師!上面推導還有一個問題!
很好,小蘿蔔同學,請說說是什麼問題。
我們在討論給目標函式$F(x)$一個增量$\Delta x$時,直接就寫成了$F(x+\Delta x)$。但是老師,這個加法可能沒有定義!
小蘿蔔同學看到了一個嚴重的問題,這確實是在先前的討論中忽略掉了。由於我們不限制頂點的型別,$x$在引數化之後,很可能是沒有加法定義的。
最簡單的就是常見的四維變換矩陣$T$或者三維旋轉矩陣$R$。它們對加法並不封閉,因為兩個變換陣之和並不是變換陣,兩個正交陣之和也不是正交陣。它們乘法的性質非常好,但是確實沒有加法,所以也不能像上面討論的那樣去求導。
但是,如果圖優化不能處理$SE(3)$或$SO(3)$中的元素,那將是十分令人沮喪的,因為SLAM要估計的機器人軌跡必須用它們來描述啊。
回想我們先前講過的李代數知識。雖然李群 $SE(3)$ 和 $SO(3)$ 是沒有加法的,但是它們對應的李代數 $\mathfrak{se}(3), \mathfrak{so}(3)$ 有啊! 數學一點地說,我們可以求它們在正切空間裡的流形上的梯度!如果讀者覺得理解困難,我們就說,通過指數變換和對數變換,先把變換矩陣和旋轉矩陣轉換成李代數,在李代數上進行加法,然後再轉換到原本的李群中。這樣我們就完成了求導。
這樣的好處是我們完全不用重新推導公式。這件事比我們想的更加簡單。在程式裡,我們只需重新定義一個優化變數$x$的增量加法即可。如果$x$是一個$SE(3)$裡的變換矩陣,我們就遵守剛才講的李代數轉換方式。當然,如果$x$是其他什麼奇怪的東東,只要定義了它的加法,程式就會自動去計算如何求它的雅可比。
核函式
又是核函式!——學過機器學習課程的同學肯定要這樣講。
但是很遺憾,圖優化中也有一種核函式。 引入核函式的原因,是因為SLAM中可能給出錯誤的邊。SLAM中的資料關聯讓科學家頭疼了很長時間。出於變化、噪聲等原因,機器人並不能確定它看到的某個路標,就一定是資料庫中的某個路標。萬一認錯了呢?我把一條原本不應該加到圖中的邊給加進去了,會怎麼樣?
嗯,那優化演算法可就慒逼了……它會看到一條誤差很大的邊,然後試圖調整這條邊所連線的節點的估計值,使它們順應這條邊的無理要求。由於這個邊的誤差真的很大,往往會抹平了其他正確邊的影響,使優化演算法專注於調整一個錯誤的值。
於是就有了核函式的存在。核函式保證每條邊的誤差不會大的沒邊,掩蓋掉其他的邊。具體的方式是,把原先誤差的二範數度量,替換成一個增長沒有那麼快的函式,同時保證自己的光滑性質(不然沒法求導啊!)。因為它們使得整個優化結果更為魯棒,所以又叫它們為robust kernel(魯棒核函式)。
很多魯棒核函式都是分段函式,在輸入較大時給出線性的增長速率,例如cauchy核,huber核等等。當然具體的我們也不展開細說了。
核函式在許多優化環境中都有應用,博主個人印象較深的時當年有一大堆人在機器學習演算法里加各種各樣的核,我們現在用的svm也會帶個核函式。
小結
最後總結一下做圖優化的流程。
- 選擇你想要的圖裡的節點與邊的型別,確定它們的引數化形式;
- 往圖裡加入實際的節點和邊;
- 選擇初值,開始迭代;
- 每一步迭代中,計算對應於當前估計值的雅可比矩陣和海塞矩陣;
- 求解稀疏線性方程$H_k \Delta x = -b_k$,得到梯度方向;
- 繼續用GN或LM進行迭代。如果迭代結束,返回優化值。
實際上,g2o能幫你做好第3-6步,你要做的只是前兩步而已。下節我們就來嘗試這件事。