視覺SLAM漫談
1. 前言
開始做SLAM(機器人同時定位與建圖)研究已經近一年了。從一年級開始對這個方向產生興趣,到現在為止,也算是對這個領域有了大致的瞭解。然而越瞭解,越覺得這個方向難度很大。總體來講有以下幾個原因:
- 入門資料很少。雖然國內也有不少人在做,但這方面現在沒有太好的入門教程。《SLAM for dummies》可以算是一篇。中文資料幾乎沒有。
- SLAM研究已進行了三十多年,從上世紀的九十年代開始。其中又有若干歷史分枝和爭論,要把握它的走向就很費工夫。
- 難以實現。SLAM是一個完整的系統,由許多個分支模組組成。現在經典的方案是“影象前端,優化後端,閉環檢測”的三部曲,很多文獻看完了自己實現不出來。
- 自己動手程式設計需要學習大量的先決知識。首先你要會C和C++,網上很多程式碼還用了11標準的C++。第二要會用Linux。第三要會cmake,vim/emacs及一些程式設計工具。第四要會用openCV, PCL, Eigen等第三方庫。只有學會了這些東西之後,你才能真正上手編一個SLAM系統。如果你要跑實際機器人,還要會ROS。
當然,困難多意味著收穫也多,坎坷的道路才能鍛鍊人(比如說走著走著才發現Linux和C++才是我的真愛之類的。)鑑於目前網上關於視覺SLAM的資料極少,我於是想把自己這一年多的經驗與大家分享一下。說的不對的地方請大家批評指正。
這篇文章關注視覺SLAM,專指用攝像機,Kinect等深度像機來做導航和探索,且主要關心室內部分。到目前為止,室內的視覺SLAM仍處於研究階段,遠未到實際應用的程度。一方面,編寫和使用視覺SLAM需要大量的專業知識,演算法的實時性未達到實用要求;另一方面,視覺SLAM生成的地圖(多數是點雲)還不能用來做機器人的路徑規劃,需要科研人員進一步的探索和研究。以下,我會介紹SLAM的歷史、理論以及實現的方式,且主要介紹視覺(Kinect)的實現方式。
2. SLAM問題
SLAM,全稱叫做Simultaneous Localization and Mapping,中文叫做同時定位與建圖。啊不行,這麼講下去,這篇文章肯定沒有人讀,所以我們換一個講法。
3. 小蘿蔔的故事
從前,有一個機器人叫“小蘿蔔”。它長著一雙烏黑髮亮的大眼睛,叫做Kinect。有一天,它被邪惡的科學家關進了一間空屋子,裡面放滿了雜七雜八的東西。

小蘿蔔感到很害怕,因為這個地方他從來沒來過,一點兒也不瞭解。讓他感到害怕的主要是三個問題:
1. 自己在哪裡?
2. 這是什麼地方?
3. 怎麼離開這個地方?
在SLAM理論中,第一個問題稱為定位 (Localization),第二個稱為建圖 (Mapping),第三個則是隨後的路徑規劃。我們希望藉助Kinect工具,幫小蘿蔔解決這個難題。各位同學有什麼思路呢?
4. Kinect資料
要打敗敵人,首先要了解你的武器。不錯,我們先介紹一下Kinect。眾所周知這是一款深度相機,你或許還聽說過別的牌子,但Kinect的價格便宜,測量範圍在3m-12m之間,精度約3cm,較適合於小蘿蔔這樣的室內機器人。它採到的影象是這個樣子的(從左往右依次為rgb圖,深度圖與點雲圖):

Kinect的一大優勢在於能比較廉價地獲得每個畫素的深度值,不管是從時間上還是從經濟上來說。OK,有了這些資訊,小蘿蔔事實上可以知道它採集到的圖片中,每一個點的3d位置。只要我們事先標定了Kinect,或者採用出廠的標定值。
我們把座標系設成這個樣子,這也是openCV中採用的預設座標系。
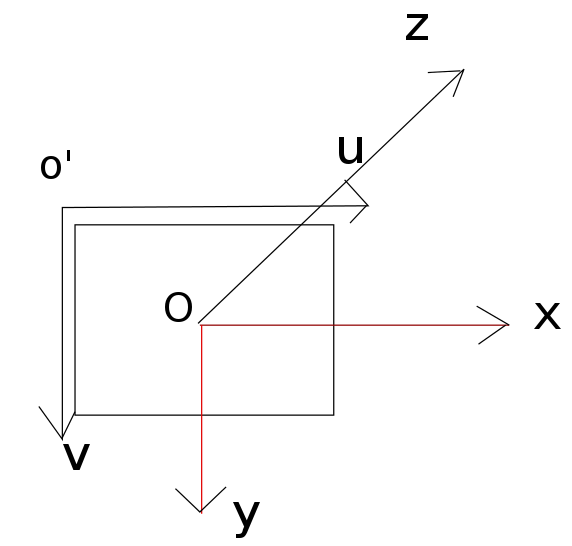
o’-uv是圖片座標系,o-xyz是Kinect的座標系。假設圖片中的點為(u,v),對應的三維點位置在(x,y,z),那麼它們之間的轉換關係是這樣的:
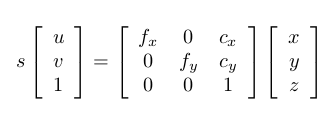
左側的s為尺度因子,表示從相機光心出去的射線都會落在成像平面的同一個點上。如果我們不知道該點的距離,那麼s就是一個自由變數。但在RGB-D相機中,我們在Depth圖中知道了這個距離,它的讀數dep(u,v)與真實距離相差一個倍數。如果也記作s,那麼:
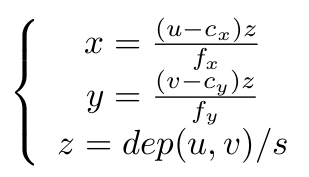
後一個公式給出了計算三維點的方法。先從深度圖中讀取深度資料(Kinect給的是16位無符號整數),除掉z方向的縮放因子,這樣你就把一個整數變到了以米為單位的資料。然後,x,y用上面的公式算出。一點都不難,就是一箇中心點位置和一個焦距而已。f代表焦距,c代表中心。如果你沒有自己標定你的Kinect,也可以採用預設的值:s=5000, cx = 320, cy=240, fx=fy=525。實際值會有一點偏差,但不會太大。
5. 定位問題
知道了Kinect中每個點的位置後,接下來我們要做的,就是根據兩幀影象間的差別計算小蘿蔔的位移。比如下面兩張圖,後一張是在前一張之後1秒採集到的:

你肯定可以看出,小蘿蔔往右轉過了一定的角度。但究竟轉過多少度呢?這就要靠計算機來求解了。這個問題稱為相機相對姿態估計,經典的演算法是ICP(Iterative Closest Point,迭代最近點)。這個演算法要求知道這兩個影象間的一組匹配點,說的通俗點,就是左邊影象哪些點和右邊是一樣的。你當然看見那塊黑白相間的板子同時出現在兩張影象中。在小蘿蔔看來,這裡牽涉到兩個簡單的問題:特徵點的提取和匹配。
如果你熟悉計算機視覺,那你應該聽說過SIFT, SURF之類的特徵。不錯,要解決定位問題,首先要得到兩張影象的一個匹配。匹配的基礎是影象的特徵,下圖就是SIFT提取的關鍵點與匹配結果:


對實現程式碼感興趣的同學請Google“opencv 匹配”即可,在openCV的教程上也有很明白的例子。上面的例子可以看出,我們找到了一些匹配,但其中有些是對的(基本平等的匹配線),有些是錯的。這是由於影象中存在週期性出現的紋理(黑白塊),所以容易搞錯。但這並不是問題,在接下來的處理中我們會將這些影響消去。
得到了一組匹配點後,我們就可以計算兩個影象間的轉換關係,也叫PnP問題。它的模型是這樣的:\[\begin{equation}\left[ \begin{array}{l}
u\\
v
\end{array} \right] = C\left( {Rp + t} \right)\end{equation}\]
R為相機的姿態,C為相機的標定矩陣。R是不斷運動的,而C則是隨著相機做死的。ICP的模型稍有不同,但原理上也是計算相機的姿態矩陣。原則上,只要有四組匹配點,就可以算這個矩陣。你可以呼叫openCV的SolvePnPRANSAC函式或者PCL的ICP演算法來求解。openCV提供的演算法是RANSAC(Random Sample Consensus,隨機取樣一致性)架構,可以剔除錯誤匹配。所以程式碼實際執行時,可以很好地找到匹配點。以下是一個結果的示例。

上面兩張圖轉過了16.63度,位移幾乎沒有。
有同學會說,那隻要不斷匹配下去,定位問題不就解決了嗎?表面上看來,的確是這樣的,只要我們引入一個關鍵幀的結構(發現位移超過一個固定值時,定義成一個關鍵幀)。然後,把新的影象與關鍵幀比較就行了。至於建圖,就是把這些關鍵幀的點雲拼起來,看著還有模有樣,煞有介事的:

1-200幀的匹配結果
然而,如果事情真這麼簡單,SLAM理論就不用那麼多人研究三十多年了(它是從上世紀90年代開始研究的)(上面講的那些東西簡直隨便哪裡找個小碩士就能做出來……)。那麼,問題難在什麼地方呢?
6. SLAM端優化理論
最麻煩的問題,就是“噪聲”。這種漸近式的匹配方式,和那些慣性測量裝置一樣,存在著累積噪聲。因為我們在不斷地更新關鍵幀,把新影象與最近的關鍵幀比較,從而獲得機器人的位移資訊。但是你要想到,如果有一個關鍵幀出現了偏移,那麼剩下的位移估計都會多出一個誤差。這個誤差還會累積,因為後面的估計都基於前面的機器人位置……哇!這後果簡直不堪設想啊(例如,你的機器人往右轉了30度,再往左轉了30度回到原來的位置。然而由於誤差,你算成了向右轉29度,再向左轉31度,這樣你構建的地圖中,會出現初始位置的兩個“重影”)。我們能不能想辦法消除這個該死的誤差呢?
朋友們,這才是SLAM的研究,前面的可以說是“影象前端”的處理方法。我們的解決思路是:如果你和最近的關鍵幀相比,會導致累計誤差。那麼,我們最好是和更前面的關鍵幀相比,而且多比較幾個幀,不要只比較一次。
我們用數學來描述這個問題。設:
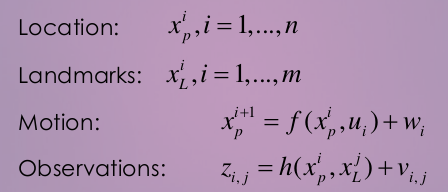
不要怕,只有藉助數學才能把這個問題講清楚。上面的公式中,xp是機器人小蘿蔔的位置,我們假定由n個幀組成。xL則是路標,在我們的影象處理過程中就是指SIFT提出來的關鍵點。如果你做2D SLAM,那麼機器人位置就是x, y加一個轉角theta。如果是3D SLAM,就是x,y,z加一個四元數姿態(或者rpy姿態)。這個過程叫做引數化(Parameterization)。
不管你用哪種引數,後面兩個方程你都需要知道。前一個叫運動方程,描述機器人怎樣運動。u是機器人的輸入,w是噪聲。這個方程最簡單的形式,就是你能通過什麼方式(碼盤等)獲得兩幀間的位移差,那麼這個方程就直接是上一幀與u相加即得。另外,你也可以完全不用慣性測量裝置,這樣我們就只依靠影象裝置來估計,這也是可以的。
後一個方程叫觀測方程,描述那些路標是怎麼來的。你在第i幀看到了第j個路標,產生了一個測量值,就是影象中的橫縱座標。最後一項是噪聲。偷偷告訴你,這個方程形式上和上一頁的那個方程是一模一樣的。
在求解SLAM問題前,我們要看到,我們擁有的資料是什麼?在上面的模型裡,我們知道的是運動資訊u以及觀測z。用示意圖表示出來是這樣的:
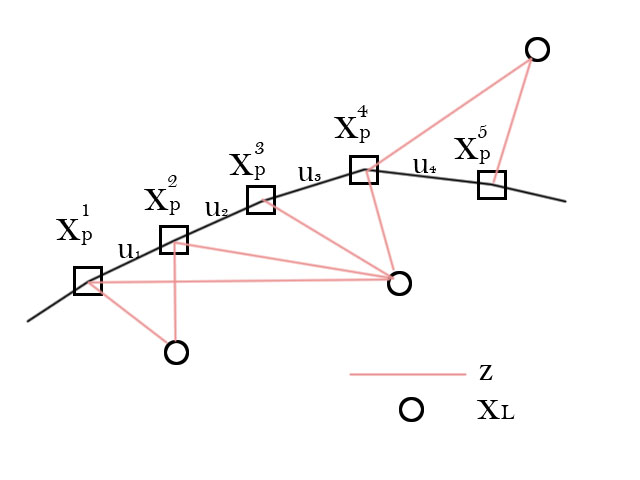
我們要求解的,就是根據這些u和z,確定所有的xp和xL。這就是SLAM問題的理論。從SLAM誕生開始科學家們就一直在解決這個問題。最初,我們用Kalman濾波器,所以上面的模型(運動方程和觀測方程)被建成這個樣子。直到21世紀初,卡爾曼濾波器仍在SLAM系統佔據最主要的地位,Davison經典的單目SLAM就是用EKF做的。但是後來,出現了基於圖優化的SLAM方法,漸漸有取而代之的地位[1]。我們在這裡不介紹卡爾曼濾波器,有興趣的同學可以在wiki上找卡爾曼濾波器,另有一篇中文的《卡爾曼濾波器介紹》也很棒。由於濾波器方法儲存n個路標要消耗n平方的空間,在計算量上有點對不住大家。儘管08年有人提出分治法的濾波器能把複雜度弄到O(n) [2],但實現手段比較複雜。我們要介紹那種新興的方法: Graph-based SLAM。
圖優化方法把SLAM問題做成了一個優化問題。學過運籌學的同學應該明白,優化問題對我們有多麼重要。我們不是要求解機器人的位置和路標位置嗎?我們可以先做一個猜測,猜想它們大概在什麼地方。這其實是不難的。然後呢,將猜測值與運動模型/觀測模型給出的值相比較,可以算出誤差:

通俗一點地講,例如,我猜機器人第一幀在(0,0,0),第二幀在(0,0,1)。但是u1告訴我機器人往z方向(前方)走了0.9米,那麼運動方程就出現了0.1m的誤差。同時,第一幀中機器人發現了路標1,它在該機器人影象的正中間;第二幀卻發現它在中間偏右的位置。這時我們猜測機器人只是往前走,也是存在誤差的。至於這個誤差是多少,可以根據觀測方程算出來。
我們得到了一堆誤差,把這些誤差平方後加起來(因為單純的誤差有正有負,然而平方誤差可以改成其他的範數,只是平方更常用),就得到了平方誤差和。我們把這個和記作phi,就是我們優化問題的目標函式。而優化變數就是那些個xp, xL。
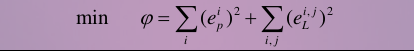
改變優化變數,誤差平方和(目標函式)就會相應地變大或變小,我們可以用數值方法求它們的梯度和二階梯度矩陣,然後用梯度下降法求最優值。這些東西學過優化的同學都懂的。
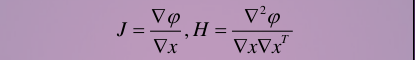
注意到,一次機器人SLAM過程中,往往會有成千上萬幀。而每一幀我們都有幾百個關鍵點,一乘就是幾百萬個優化變數。這個規模的優化問題放到小蘿蔔的機載小破本上可解嗎?是的,過去的同學都以為,Graph-based SLAM是無法計算的。但就在21世紀06,07年後,有些同學發現了,這個問題規模沒有想象的那麼大。上面的J和H兩個矩陣是“稀疏矩陣”,於是呢,我們可以用稀疏代數的方法來解這個問題。“稀疏”的原因,在於每一個路標,往往不可能出現在所有運動過程中,通常只出現在一小部分影象裡。正是這個稀疏性,使得優化思路成為了現實。
優化方法利用了所有可以用到的資訊(稱為full-SLAM, global SLAM),其精確度要比我們一開始講的幀間匹配高很多。當然計算量也要高一些。
由於優化的稀疏性,人們喜歡用“圖”來表達這個問題。所謂圖,就是由節點和邊組成的東西。我寫成G={V,E},大家就明白了。V是優化變數節點,E表示運動/觀測方程的約束。什麼,更糊塗了嗎?那我就上一張圖,來自[3]。
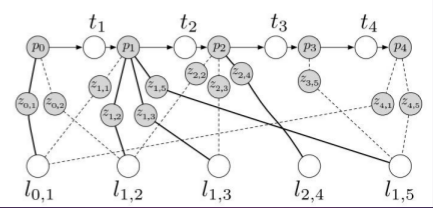
圖有點模糊,而且數學符號和我用的不太一樣,我用它來給大家一個圖優化的直觀形象。上圖中,p是機器人位置,l是路標,z是觀測,t是位移。其中呢,p, l是優化變數,而z,t是優化的約束。看起來是不是像一些彈簧連線了一些質點呢?因為每個路標不可能出現在每一幀中,所以這個圖是蠻稀疏的。不過,“圖”優化只是優化問題的一個表達形式,並不影響優化的含義。實際解起來時還是要用數值法找梯度的。這種思路在計算機視覺裡,也叫做Bundle Adjustment。它的具體方法請參見一篇經典文章[4]。
不過,BA的實現方法太複雜,不太建議同學們拿C來寫。好在2010年的ICRA上,其他的同學們提供了一個通用的開發包:g2o [5]。它是有圖優化通用求解器,很好用,我改天再詳細介紹這個軟體包。總之,我們只要把觀測和運動資訊丟到求解器裡就行。這個優化器會為我們求出機器人的軌跡和路標位置。如下圖,紅點是路標,藍色箭頭是機器人的位置和轉角(2D SLAM)。細心的同學會發現它往右偏轉了一些。:

7. 閉環檢測
上面提到,僅用幀間匹配最大的問題在於誤差累積,圖優化的方法可以有效地減少累計誤差。然而,如果把所有測量都丟進g2o,計算量還是有點兒大的。根據我自己測試,約10000多條邊,g2o跑起來就有些吃力了。這樣,就有同學說,能把這個圖構造地簡潔一些嗎?我們用不著所有的資訊,只需要把有用的拿出來就行了。
事實上,小蘿蔔在探索房間時,經常會左轉一下,右轉一下。如果在某個時刻他回到了以前去過的地方,我們就直接與那時候採集的關鍵幀做比較,可以嗎?我們說,可以,而且那是最好的方法。這個問題叫做閉環檢測。
閉環檢測是說,新來一張影象時,如何判斷它以前是否在影象序列中出現過?有兩種思路:一是根據我們估計的機器人位置,看是否與以前某個位置鄰近;二是根據影象的外觀,看它是否和以前關鍵幀相似。目前主流方法是後一種,因為很多科學家認為前一種依靠有噪聲的位置來減少位置的噪聲,有點迴圈論證的意思。後一種方法呢,本質上是個模式識別問題(非監督聚類,分類),常用的是Bag-of-Words (BOW)。但是BOW需要事先對字典進行訓練,因此SLAM研究者仍在探討有沒有更合適的方法。
在Kinect SLAM經典大作中[6],作者採用了比較簡單的閉環方法:在前面n個關鍵幀中隨機採k個,與當前幀兩兩匹配。匹配上後認為出現閉環。這個真是相當的簡單實用,效率也過得去。
高效的閉環檢測是SLAM精確求解的基礎。這方面還有很多工作可以做。
8. 小結
本文我們介紹了SLAM的基本概念,重點介紹了圖優化解決SLAM問題的思路。我最近正在編寫SLAM程式,它是一個Linux下基於cmake的工程。目前仍在開發當中。歡迎感興趣的同學來交流研究心得,我的郵件是:gaoxiang12@mails.tsinghua.edu.cn。
參考文獻
[1] Visual SLAM: Why filter? Strasdat et. al., Image and Vision Computing, 2012.
[2] Divide and Conquer: EKF SLAM in O(n), Paz Lina M et al., IEEE Transaction on Robotics, 2008
[3] Relative bundle adjustment, Sibley, Gabe, 2009
[4] Bundle adjustment - a Modern Synthesis. Triggs B et. el., Springer, 2000
[5] g2o: A General Framework for Graph Optimization, Kummerle Rainer, et. al., ICRA, 2011
[6] 3-D Mapping with an RGB-D Camera, IEEE Transaction on Robotics, Endres et al., 2014