視覺SLAM中的數學基礎 第一篇 3D空間的位置表示
前言
轉眼間一個學期又將過去,距離我上次寫《一起做RGBD SLAM》已經半年之久。《一起做》系列反響很不錯,主要由於它為讀者提供了一個可以一步步編碼、執行的SLAM程式,為讀者理解SLAM實現的細節作了詳細的介紹。但是我也有很多對它不滿意的地方。作為面向實現的介紹,它的程式碼不夠穩定可靠,例如,甚至沒有對匹配丟失的情況進行處理,因而只能用於教學。另一方面,對SLAM研究者來說,我只是介紹了編碼方面如何呼叫一些常見的庫函式,而沒有對這些函式進行深入的,原理上的講解。這就導致了讀者只瞭解了函式的介面,而沒法根據數學原理進行創新。歸根到底,研究機器人相關問題,一是要有紮實的數學基礎,二是要有強大的動手程式設計能力,這對大多數剛入門的研究者來說,極具挑戰性。我也希望,通過閱讀我的部落格,你能走進SLAM研究的門檻,有朝一日自己也寫出優秀的程式和論文。
有鑑於此,我準備寫一寫SLAM相關的數學知識,包括代數、幾何、概率、運籌等等。對於重要的演算法例如ICP,EKF,細緻討論它的原理,並給出它的實現(原生的程式碼或在某個庫的實現)。由於它們的原理較複雜,我會從最基本的東西開始講起。但是我畢竟不是在寫數學書,我不會像數學書那樣寫成``定義——定理——推論”的結構。我們不會糾纏於一些定理的嚴格證明,相反的,我們只在必要的情況下加以說明,告訴讀者這些數學公式在SLAM中有何應用,如何應用。
由於部落格編輯器的限制,我們以斜體字$x$表示變數,以粗正體$\mathbf{A}$表示向量和字母,以黑板粗體$\mathbb{R}$表示空間。希臘字母沒有粗體所以保持原樣。向量預設為列向量。其餘和普通的數學書一致。
小蘿蔔:師兄,這麼嚴肅不是你的風格啊!
師兄:啊,數學嘛……
剛體運動
本篇我們討論一個很基礎的問題:如何描述機器人的位姿。這也是研究SLAM的第一個問題。注意這裡“位姿”的用語包含了位置和姿態。描述位置是很簡單的。如果機器人在平面內運動,那麼用兩個座標來描述它的位置:$$ \mathbf{x} = \left[ x, y \right]^T.$$ 相應的,如果它在三維空間中,我們就用三個空間座標來表示:$$ \mathbf{x} = \left[ x, y, z \right].$$
姿態的表達比點稍為複雜。2D的姿態可以只用一個旋轉角$\theta$表達。3D姿態的表達方式則有多種。常見的如尤拉角、四元數、旋轉矩陣等。我們將在後文詳細介紹。有了位置和姿態,我們就可以描述一個座標系。進一步,還能描述座標系間的變換關係。常見的問題如:機器人視野中某個點,對世界座標系的(或地圖的)哪個點?這時,就需要先得到該點針對機器人座標系座標值,再根據機器人位姿轉換到世界座標系中。
齊次座標系
在位姿轉換中,通常採用射影空間的齊次座標表示。齊次座標是什麼呢?記$n$維射影空間為$\mathbb{P}^n$,其中一個空間點的座標為普通的3D座標加一個齊次分量:$$ \mathbf{x}=\left[ x_1, \ldots, x_n, w \right]^T. $$ 例如,在2維和3維射影空間中的點,分別表示為:
\[\begin{equation}
\mathbf{x}_{2D} = \left[x, y, w \right]^T \quad \mathbf{x}_{3D} = \left[ x, y, z, w \right]^T
\end{equation}\]
小蘿蔔:既然一個空間點只有3個座標,為啥非要用四個數表示呢?
師兄:嗯,四個數表示點,說明點和座標肯定不是一一對應的。沒錯,在齊次座標中,某個點$\mathbf{x}$的每個分量同乘一個非零常數$k$後,仍然表示的是同一個點。因此,一個點的具體座標值不是唯一的。如$\left[1,1,1,1\right]^T$和$\left[2,2,2,2\right]^T$是同一個點。但在$w \neq 0$時,我們可以對每個座標除以最後一項$w$,強制最後一項為1,從而得到一個點唯一的座標表示:
\[\begin{equation}
\mathbf{x}_{3D} = \left[ x/w, y/, z/w, 1 \right]^T
\end{equation}\]
這時,忽略掉最後一項,這個點的座標和歐氏空間就是一樣的。那麼,為要用齊次座標呢?原因有以下幾條。
- 齊次座標下點和直線(高維空間裡為超平面)能夠使用同樣的表達。
例如,3D空間$\mathbb{R}^3$中,一個平面$\pi$可由一個方程定義:
\[\begin{equation}
\pi : ax + by + cz + d = 0
\end{equation}\]
則該平面$\pi$可以用$\mathbb{P}^3$中的座標$\mathbf{\pi} = \left[ a,b,c,d \right]^T$來描述。這樣,點位於平面上(2D對應點位於直線上)的事情可以簡潔地表示為:
\[\begin{equation}
\label{eq:pointOnPlane}
\mathbf{\pi}^T \mathbf{x} = 0.
\end{equation}\]
把點和超平面採用同樣的表示,這種做法一個非常直接的好處,是射影幾何裡的“對偶原理”。該原理是說,任何有關“點”與“平面”的命題,都可以交換“點”與“平面”的概念,得到一個對偶的命題。對偶命題和原命題是一樣的。通過“對偶原理”,射影幾何的數學家就可以偷懶,只需要證一半定理,因為對偶命題和原命題有同樣的涵義。例如,我們證明了$\mathbb{P}^2$中某條件下三點共線,那麼替換概念後的三線共點則自然成立。
小蘿蔔:數學家真是好懶啊!
- 齊次座標能囊括無窮遠點與無窮遠超平面。
最後一項座標為零的點稱為無窮遠點,它們在$\mathbb{P}^n$中真實存在,且能夠很方便地參與正常的代數運算。根據式\ref{eq:pointOnPlane},易見所有無窮遠點都在一個平面$\mathbf{\pi}_\infty = \left[ 0, 0, 0, 1\right]^T$上,該平面記作無窮遠平面(2D對應無窮遠直線)。
$\mathbb{P}^2$中的無窮遠直線較容易理解。它就像是地平線,與所有直線相交於位於它之上的無窮遠點。而且,在射影變換中(例如照相),很容易在照片中看到地平線並算出它的方程。這說明2D射影變換會把無窮遠線變成通常的直線。
- 齊次座標可以方便地將平移與旋轉放在一個矩陣中。
師兄:這應該是最明顯的好處啦!大家都愛用齊次座標,包括我。有關座標系怎麼用齊次座標進行變換,後文會詳細解釋。現在我們能表達點了,還剩下一個姿態。由於2D與3D差別較大,我們分而述之。
2D姿態的描述
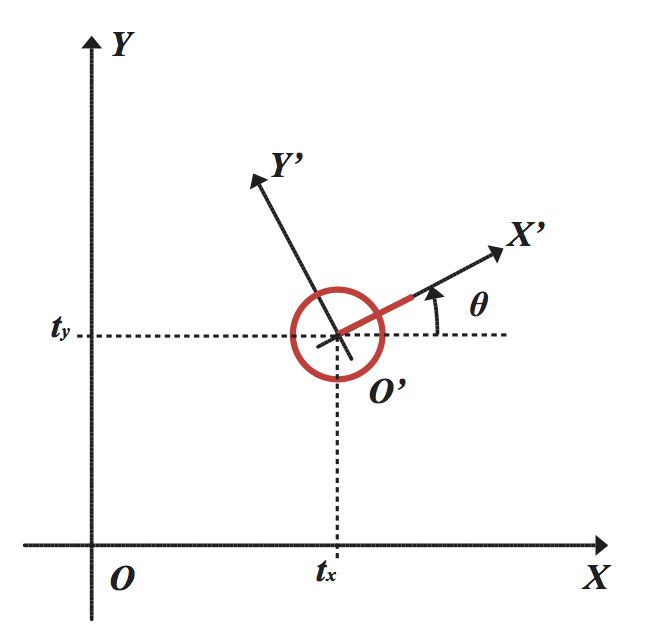
2D空間中,物體的位姿可用兩個平移量$t_x, t_y$加一個旋轉角$\theta$表示,如下圖所示。此時,設機器人座標系$O'-X'-Y'$下某點的座標為$\left[ x_r, y_r\right]^T$,對應在世界座標系$O-X-Y$下為$\left[x_w, y_w\right]^T$,那麼由直觀推得:
\[\begin{equation}
\left\{ \begin{array}{l}
{x_w} = {x_r}\cos \theta - {y_r}\sin \theta + {t_x}\\
{y_w} = {x_r}\sin \theta + {y_r}\cos \theta + {t_y}
\end{array} \right.
\end{equation}\]
讀者可以自行嘗試推導一下,在虛線處建立一箇中間座標系即可。若將該式寫成矩陣形式,則有:
\[\begin{equation}
\label{eq:2dTransRT}
\mathbf{x}_w = \mathbf{R} \mathbf{x}_r + \mathbf{t}
\end{equation}\]
其中
$$\mathbf{R} = \left[ {\begin{array}{*{20}{c}}
{\cos \theta }& - \sin \theta \\
{\sin \theta }&{\cos \theta }
\end{array}} \right], \quad \mathbf{t} = \left[ t_x, t_y\right]^T$$
$\mathbf{R}$稱為旋轉矩陣,$\mathbf{t}$為平移向量。注意到$\mathbf{R}$是一個正交矩陣,且只有一個自由度。加上平移向量後,一共有三個自由度。
此定義下的旋轉陣必是正交陣。而正交陣並非全是旋轉矩陣。事實上,行列式為$+1$的正交陣才是旋轉矩陣,行列式為$-1$的正交陣是映象後的旋轉矩陣。
式\ref{eq:2dTransRT}中,$\mathbf{x}_w$和$\mathbf{x}_r$還不是線性關係。下面我們用齊次座標表示它們,即:
$$ \mathbf{x}_w = \left[ x_w, y_w, 1\right]^T, \mathbf{x}_r = \left[ x_r, y_r, 1\right]^T $$
則有:
\[\begin{equation}
{\mathbf{x}_w} = \left[ {\begin{array}{*{20}{c}}
\mathbf{R}_{2 \times 2} & \mathbf{t}_{2 \times 1 }\\
\mathbf{0}^T_{1 \times 2} & I_{1 \times 1}
\end{array}} \right]{\mathbf{x}_r}
\end{equation}\]
為便於理解,我們在矩陣下方標出了它的維數。可以看使用齊次座標標滿足了線性關係,記作:
\[\begin{equation}
\mathbf{x}_w = \mathbf{T}_{w,r} \mathbf{x}_r
\end{equation}\]
其中$\mathbf{T}_{w,r}$表示從世界座標系到機器人座標系的變換矩陣。我們也可以輕鬆地寫出反向的變換矩陣:
\[\begin{equation}
\mathbf{x}_r = \mathbf{T}_{r,w} \mathbf{x}_w = \mathbf{T}^{-1}_{w,r} \mathbf{x}_w = \left[ {\begin{array}{*{20}{cc}}
{{\mathbf{R}^{ - 1}}}&{{-\mathbf{R}^{ - 1}} \mathbf{t}}\\
{{0^T}} & 1
\end{array}} \right] \mathbf{x}_w
\end{equation}\]
既然如此,我們就可用$\mathbf{T}$表示機器人的位姿,那麼機器人在時刻$t$的位姿就可以記作$\mathbf{T}_t$。當然,從儲存上來講,儲存$\mathbf{T}$是不經濟的。在2D運動中,它有九個變數,但實際自由度只有三個。所以我們可以只儲存位移向量$\mathbf{t}$與旋轉角$\theta$,而在需要計算的時候再構建出$\mathbf{T}$。稱2D歐幾里得變換,它對矩陣乘法構成群(群是一個集合加一種運算,且運算在該集合上滿足封閉性、結合律、有單位元和逆元。),該群記作$SE(2)$。相應的,二維旋轉構成二維旋轉群(或稱特殊正交群)$SO(2)$。有關它們進一步的性質,我們會在以後的李群、李代數中提到。
3D變換
3D的旋轉可以由旋轉矩陣、尤拉角、四元數等若干種方式描述,它們也統稱為三維旋轉群$SO(3)$。而3D的變換即旋轉加上位移,是為$SE(3)$。為了和2D變換統一起見,我們首先介紹旋轉矩陣表示法。
旋轉矩陣描述
旋轉矩陣是一種$3\times 3$的正交矩陣,它對變換的描述十分類似於2D情形。參照上一節的數學符號,我們有:
\[\begin{equation}
{\mathbf{x}_w} = \left[
{\begin{array}{*{20}{c}}
\mathbf{R}_{3 \times 3} & \mathbf{t}_{3 \times 1 }\\
\mathbf{0}^T_{1 \times 3} & 1_{1 \times 1}
\end{array}} \right]{\mathbf{x}_r}
\end{equation}\]
這裡$\mathbf{R}$為3D的旋轉矩陣,同樣的,$\mathbf{t}$為3D的平移向量。
由於3D旋轉都可以歸結成按照某個單位向量$\mathbf{n}$進行大小為$\theta$的旋轉。所以,已知某個旋轉時,可以推匯出對應的旋轉矩陣。該過程由羅德里格斯公式表明,由於過程比較複雜,我們在此不作贅述,只給出轉換的結果:
\[\begin{equation}
\mathbf{R}(\mathbf{n}, \theta) = \left[ {\begin{array}{*{20}{c}}
{n_x^2\left( {1 - c\theta } \right) + c\theta }&{{n_x}{n_y}\left( {1 - c\theta } \right) + {n_z}s\theta }&{{n_x}{n_z}\left( {1 - c\theta } \right) - {n_y}s\theta }\\
{{n_x}{n_y}\left( {1 - c\theta } \right) - {n_z}s\theta }&{n_y^2\left( {1 - c\theta } \right) + c\theta }&{{n_y}{n_z}\left( {1 - c\theta } \right) + {n_x}s\theta }\\
{{n_x}{n_z}\left( {1 - c\theta } \right) + {n_y}s\theta }&{{n_y}{n_z}\left( {1 - c\theta } \right) - {n_x}s\theta }&{n_z^2\left( {1 - c\theta } \right) + c\theta }
\end{array}} \right]
\end{equation}\]
這裡$\mathbf{n} = \left[ n_x, n_y, n_z\right]^T, c\theta=\cos \theta, s\theta=\sin \theta$。公式雖然較為複雜,但實際寫成程式後,只需知道旋轉方向和角度後即可完成計算。另一件有趣的事是,如果用$$\mathbf{n}^{\wedge} = \left[ {\begin{array}{*{20}{c}}
0&{ - {n_z}}&{{n_y}}\\
{{n_z}}&0&{ - {n_x}}\\
{ - {n_y}}&{{n_x}}&0
\end{array}} \right] $$表示與$\mathbf{n}$對應的一個反對稱矩陣,那麼有:
\[\begin{equation}
\mathbf{R} (\mathbf{n}, \theta ) = \cos \theta \mathbf{I} + (1-\cos \theta ) \mathbf{n} \mathbf{n}^T + \sin \theta \mathbf{n}^{\wedge} = \exp ( \theta \mathbf{n}^{\wedge} )
\end{equation}\]
最後那個指數,讀者若不理解,可以暫時不管它,這將在之後的李代數中會講到。根據此式,我們也可以從任意給定的旋轉矩陣,求出對應的轉軸與轉角。關於轉角$\theta$,我們對上式兩邊求矩陣的跡,可得:
\[\begin{equation}
\begin{array}{lll}
tr\left( \mathbf{R} \right) &=& \cos \theta tr\left( \mathbf{I} \right) + \left( {1 - \cos \theta } \right)tr\left( { \mathbf{n} {\mathbf{n}^T}} \right) + \sin \theta tr({\mathbf{n}^ \wedge })\\
&=& 3\cos \theta + (1 - \cos \theta )\\
&=& 1 + 2\cos \theta
\end{array}
\end{equation}\]
因此:
\[\begin{equation}
\theta = \arccos ( \frac{1}{2} [ tr(\mathbf{R}) - 1 ] )
\end{equation}\]
關於轉軸$\mathbf{n}$,由於旋轉軸上的向量在旋轉後不發生改變,說明$$\mathbf{R} \mathbf{n} = \mathbf{n}. $$
因此,只要求此方程的解向量即可。這也說明$\mathbf{n}$是$\mathbf{R}$特徵值為$1$的一個特徵向量。
總之,讀者應當明白在3D時,旋轉和平移仍可用轉移矩陣$\mathbf{T}$來描述,其結構也與2D類似。而$\mathbf{T}_{4\times 4}$構成了三維歐氏變換群$SE(3)$。注意到$\mathbf{T}$雖然有16個變數,但真正的自由度只有6個,其中3個旋轉,3個位移。
旋轉矩陣描述是一種比較適合數學推導及計算機實現的方式,但它不符合人類的思維方式。當你看到一個$3 \times 3$的矩陣時,很難想象物體實際上發生了怎樣的旋轉。反之,給定一個旋轉方式,人也很難直接寫出矩陣的數值。所以,為了便於人類理解,人們還使用了其他方法來表示三維旋轉。
尤拉角
尤拉角是一種廣為使用的姿態描述方式,以直觀見長。在最常用的尤拉角表達方式中,我們把旋轉分解成沿三個軸轉動的量:滾轉角-俯仰角-偏航角(roll-pitch-yaw)。它的好處是十分的直觀,且只有三個引數描述。缺點是會碰到著名的萬向鎖問題:在俯仰為$\pm 90 ^\circ $時,表達某個姿態的形式不唯一。此外,它也不易於插值和迭代。
我們並不會詳細介紹尤拉角,因為它在SLAM中用處也很有限。我們既不會在數學推導中使用它,也不會在程式中用尤拉角表示機器人的姿態。不過,在您想驗證自己演算法輸出的姿態是否有錯時,轉換成尤拉角能讓你快速辨認結果是否有錯。
四元數
四元數原理和各種運算將在下一篇部落格中提到。
本篇小結
本篇部落格介紹了2D和3D空間中剛體運動的表示方法,以旋轉矩陣為主。下一篇我們將介紹四元數表示法,然後演示如何用Eigen3對這些矩陣進行操作。敬請期待。
如果你覺得我的部落格有幫助,可以進行幾塊錢的小額贊助,幫助我把部落格寫得更好。