2. 選擇排序—堆排序(Heap Sort)
堆排序是一種樹形選擇排序,是對直接選擇排序的有效改進。
基本思想:
堆的定義如下:具有n個元素的序列(k1,k2,...,kn),當且僅當滿足
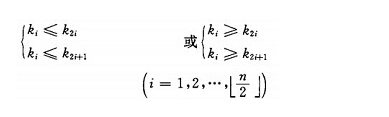
時稱之為堆。由堆的定義可以看出,堆頂元素(即第一個元素)為最小項(小頂堆)。
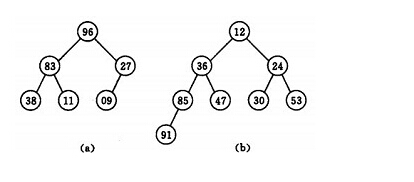
若以一維陣列儲存一個堆,則堆對應一顆完全二叉樹,且所有非葉節點的值均不大於(或不小於)其子女的值,根節點的值(堆頂元素)的值是最小(或最大)的。如:
(a)大堆頂序列(96,83,27,38,11,09)
(b)小堆頂序列(12,36,24,85,47,30,53,91)
初始時把要排列的的n個數的序列看做是一顆順序儲存的二叉樹(一維陣列儲存二叉樹),調整他們的儲存序,使之成為一個堆。將堆頂元素輸出,得到n個元素中最小(或最大)的元素,這時堆的根節點的數最小(或最大)。然後對前面的n-1個元素重新調整使之成為堆,輸出堆頂元素,得到n個元素中次小(或次大)的元素。依此類推,知道只有倆個節點的堆,並對他們做交換,最後得到n個節點的有序序列,稱這個過程為堆排序。
因此,實現堆排序需要解決倆個問題:
1、如何將n個待排序的數建成堆。
2、輸出堆頂元素後,怎樣調整剩餘n-1個元素,使其成為堆。
首先,我們討論第二個問題:輸出堆頂元素後,對剩餘的n-1個元素重新建成堆的調整過程。
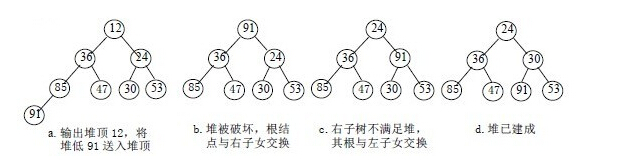
調整小堆頂的方法(大堆頂也是一樣的道理):
1、設有m個元素的堆,輸出堆頂元素後,剩下m-1個元素。將堆底元素送入堆頂(最後一個元素與堆頂元素進行交換),堆被破壞,其原因僅是根節點不滿足堆的性質。
2、將目前最新的根節點與左、右子數中較小元素進行交換。
3、若與左子數交換:如果左子數堆被破壞,即左子數的根節點不滿足堆的性質,則重複方法(2)。
4、若與右子數交換,如果右子數堆被破壞,即右子數的根節點不滿足堆的性質。則重複方法(2)。
5、繼續對不滿足堆性質的子數進行上述交換操作,知道葉子節點,堆被建成。
稱這個字根節點到葉子節點的調整過程稱為篩選。如圖:
再討論對n個元素初始建堆的過程。
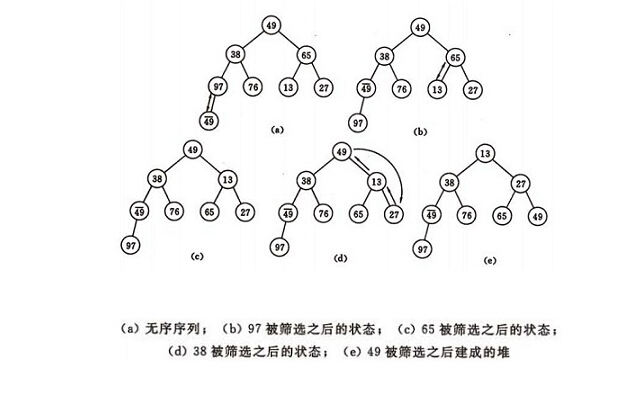
建堆方法:對初始序列建堆的過程,就是一個反覆進行篩選的過程。
1、n個節點的完全二叉樹,則最後一個節點是n/2個節點的子數。
2、篩選從第n/2個節點為根的子數開始,該子數成為堆。
3、之後向前一次對各節點為根的子數進行篩選,使之成為堆,直到根節點。
如圖建堆的初始過程:無序序列:(49,38,65,97,76,13,27,49)
演算法的實現:
從演算法的描述來看,堆排序需要倆個過程,一是建立堆,二是堆頂與堆的最後一個元素交換位置。所以,堆排序有倆個函式組成,一是建堆的滲透函式,二是反覆呼叫滲透函式實現排序的函式。
public class HeapSort { public static void main(String[] args) { int[] a = {12,54,76,23,435,98,21,1,2,23,54,76,34,2,78,243}; heapSort(a, a.length); for(int i=0; i<a.length; i++){ System.out.print(a[i]+" "); } } /** * 堆排序演算法 * */ public static void heapSort(int[] a,int length){ buildingHeap(a, a.length); //初始堆 for(int i=length-1; i>0; --i){ int temp = a[i]; a[i] = a[0]; a[0] = temp; heapAdjust(a, 0, i); } } /** * 初始堆進行調整 * 將a[0..length-1]建成堆 * 調整完之後第一個元素師序列的最小元素 * */ public static void buildingHeap(int[] a,int length){ //最後一個有孩子的節點的位置i = length/2 - 1 for(int i=(length/2)-1; i>=0; --i){ heapAdjust(a, i, length); } } /** * 已知a[a...m]除了a[s]外均滿足堆的定義 * 調整a[s],使其成為大頂堆,即將對第s個節點為根的子數帥選 * * @param a是待調整的陣列 * @param s是待調整的陣列元素的位置 * @param length是陣列的長度 * */ public static void heapAdjust(int[] a,int s,int length){ int temp = a[s]; int child = 2*s+1; //左孩子節點的位置。 while(child < length){ if(child+1 < length && a[child] <a[child+1] ){//如果右孩子大於左孩子(找到比當前待調整節點大的孩子) ++ child; } if(a[s]<a[child]){//如果較大的子節點大於父節點 a[s] = a[child];//那麼把較大的子節點往上移動,替換他的父節點 s = child; //重新設定s,即待調整的下一個節點的位置 child = 2*s+1; }else{ //如果當前待調整節點大於他的左右孩子,則不需要調整,直接退出 break; } a[s] = temp;//當前待調整的節點放到比其大的孩子的節點的位置上 } } }
演算法分析:
設數深度為k,k=log2n+1。從根到葉的篩選,元素比較次數之多2(k-1)次,交換記錄之多k次。所以,在建好堆後,排序過程中的次數不超過下式:
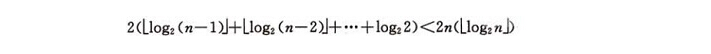
而建堆的比較次數不超過4n次,因此堆排序最壞情況下,時間複雜度也為:O(nlogn)。