八大排序簡單小結及c++實現
即插入排序、氣泡排序、選擇排序、shell排序、基數排序、歸併排序、快速排序、堆排序
一、(直接)插入法(交換排序)
1、原理方法
從第二個數開始與前面的一個一個比較,小於則交換、大於等於則下一個數的迴圈。
2、特點
1)、穩定性:穩定
2)、時間代價:O(n*n)
最好——正序——時間代價Θ(n)
最差——倒序——時間代價Θ(n*n)
平均——亂序——時間代價Θ(n*n)
3)、輔助儲存空間:O(1)
4)、比較
①較為複雜、速度較慢
②n較小時(如<=50) 、區域性或整體有序時適用
插入排序的最佳時間代價特性——基本有序。
③迴圈交換
迴圈不同:f(n)<=1/2*n*(n-1)<=1/2*n*n
交換不同(賦值操作)
3、程式碼
#include <iostream>
using namespace std;
void InsertSort(int* , int );
int main()
{
int data[]={1,-30,12,7,-1,5,4};
InsertSort(data,7);
for(int i=0;i<7;i++)
cout<<dec<<data[i]<<" ";
cout<<"\n";
//system ( "pause" );//getchar();
return 0;
}
void InsertSort(int* pData,int Count)
{
int iTemp;
int iPos;
for(int i=1;i<Count;i++)
{
iPos=i-1;
iTemp=pData[i];
while((iPos>=0)&&(iTemp<pData[iPos]))
{
pData[iPos+1]=pData[iPos];
iPos--;
}
pData[iPos+1]=iTemp;
}
}二、冒泡法(交換排序)
1、原理方法
1)、把小的元素往前調或者把大的元素往後調, 一趟得到一個最大值或最小值。
若迴圈外設一個bool變數、最差(倒序)迴圈n-1趟、最好(正序)迴圈一趟
2)、有遞迴和非遞迴實現
2、特點
1)、穩定性:穩定
2)、時間代價:
最好——正序、無交換(O(0))——時間代價Θ(n)(只迴圈一趟)
最差——倒序、迴圈次數=交換次數(O(n*n))——時間代價Θ(n*n)
平均——亂序、中間狀態 ——時間代價Θ(n*n)
3)、輔助儲存空間:O(1)
4)、比較
①速度較慢、交換次數相對比較多
②n較小時(如<=50) ,區域性或整體有序時、較快
③迴圈交換
迴圈相同(若迴圈外不設判斷條件):
1+2+...+n-1=1/2*(n-1)*n<=1/2*n*n=K*g(n)
f(n)=O(g(n))=O(n*n)(迴圈複雜度)
交換不同
3、程式碼
1)、非遞迴迴圈實現
#include <iostream>
using namespace std;
void BubbleSort(int* , int );
int main()
{
int data[]={10,9,13,7,32,5,2};
BubbleSort(data,7);
for(int i=0;i<7;i++)
cout<<dec<<data[i]<<" ";
cout<<"\n";
return 0;
}
void BubbleSort(int* pData,int n)
{
int iTemp;
bool bFilish=fale;
for(int i=0;i<n-1;i++)
{
if(bFlish=true)
break;
bFilish=true;
for(int j=n-1;j>i;j--)
{
if(pData[j]<pData[j-1])
{
iTemp=pData[j-1];
pData[j-1]=pData[j];
pData[j]=iTemp;
bFilish=false;
}
}
}
}
#include <iostream>
using namespace std;
void BilateralBubbleSort(int* , int,int );
int main()
{
int data[]={10,9,13,7,32,5,2};
BilateralBubbleSort(data,0,6);
for(int i=0;i<7;i++)
cout<<dec<<data[i]<<" ";
cout<<"\n";
return 0;
}
void BilateralBubbleSort(int *a, int first, int last)
{
if (first >= last) //退出條件
{
return;
}
int i = first;
int j = last;
int temp = a[first];
while (i != j)
{
while (i<j && a[j]>=temp)
{
j--;
}
a[i] = a[j];
while (i<j && a[i]<=temp)
{
i++;
}
a[j] = a[i];
}
a[i] = temp;
//遞迴,有點像快速排序,就是中間值放在臨時變數而不是陣列尾部
BilateralBubbleSort(a, first, i-1);
BilateralBubbleSort(a, i+1, last);
}
三、(簡單或直接)選擇法(交換排序)
1、原理方法
1)、第一個元素開始,同其後的元素比較並記錄最小值(放在當前位置)。
每次得到一個最小值
2)、(改進)選擇中間變數、減少交換次數
2、特點
1)、穩定性:不穩定
2)、時間代價:O(n*n)
最好——正序、無交換(O(0))
最差——倒序、迴圈次數=交換次數
平均—— 亂序、中間狀態
3)、輔助儲存空間:O(1)
4)、比較
①速度較慢
②與冒泡法某些情況下稍好,在某些情況下稍差
這3種中是很有效的, n較小時(如<=50) 適用
③迴圈交換
迴圈相同:
1/2*(n-1)*n
交換不同
3、程式碼
#include <iostream>
using namespace std;
void SelectSort(int* , int );
int main()
{
int data[]={1,9,12,7,26,5,4};
SelectSort(data,7);
for(int i=0;i<7;i++)
cout<<dec<<data[i]<<" ";
cout<<"\n";
return 0;
}
void SelectSort(int* pData,int Count)
{
int iTemp;
for(int i=0;i<Count-1;i++)
{
for(int j=i+1;j<Count;j++)
{
if(pData[i]<pData[j])
{
iTemp=pData[i];
pData[i]=pData[j];
pData[j]=iTemp;
}
}
}
}四、快速排序
1、原理方法
1)、分治法
2)、二叉查詢樹
像一個二叉樹、遞迴實現
①(分割)首先選擇一個軸值,如放在陣列最後
②把比它小的放在左邊,大的放在右邊(兩端移動下標,找到一對後交換)。
③直到相遇、返回下標k(右半部起始、即軸值下標)
④然後對兩邊分別使用這個過程
3)、軸值的選取
①第一個記錄的關鍵碼(正、逆序時有問題)
②隨機抽取軸值(開銷大)
③陣列中間點(一般)
4)、最理想的情況
①陣列的大小是2的冪,這樣分下去始終可以被2整除
假設為2的k次方,即k=log2(n)。
②每次我們選擇的值剛好是中間值、陣列可以被等分。
第一層遞迴,迴圈n次,第二層迴圈2*(n/2)......
所以共有n+2(n/2)+4(n/4)+...+n*(n/n) = n+n+n+...+n=k*n=log2(n)*n
所以演算法複雜度為O(n*log2(n))
其他的情況只會比這種情況差,最差的情況是每次選擇到的middle都是最小值或最大值,那麼他將變成交換法(由於使用了遞迴,情況更糟)。
2、特點
1)、穩定性:不穩定
2)、時間代價:O(n*logn)
最差——O(n*n)
平均——O(n*logn),介於最佳和最差之間
最好——O(n*logn)
3)、輔助儲存空間:O(logn)
4)、比較
①區域性或整體有序時慢
②(大多數情況)平均最快
n(≥9)較大時、關鍵字元素比較隨機(雜亂無序)適用
③分割陣列,多交換、少比較
3、程式碼
1)、一般的方法
#include<iostream>
using namespace std;
typedef int* IntArrayPtr;
int Divide(int a[],int left,int right)
{
int k=a[left]; //軸值
do
{
while(left<right&&a[right]>=k) --right;
if(left<right)
{
a[left]=a[right];
++left;
}
while(left<right&&a[left]<=k)++left;
if(left<right)
{
a[right]=a[left];
--right;
}
}while(left!=right);
//排序後軸值位置,分為兩個子序列
a[left]=k;
return left;
}
void QuickSort(int a[],int left,int right)
{
int mid;
if(left>=right)return;
mid=Divide(a,left,right);
cout<<a[mid]<<'\n';
for(int j=left;j<=right;j++)
cout<<a[j]<<" ";
cout<<'\n';
//軸值左半部分
QuickSort(a,left,mid-1);
//軸值右半部分
QuickSort(a,mid+1,right);
}
void FillArray(int a[],int size)//輸入資料
{
cout<<"請輸入"<<size<<"個整數,數字之間用空格隔開:"<<endl;
for(int index=0;index<size;index++)
cin>>a[index];
}
void main()
{
int array_size;
cout<<"請輸入需要排序的元素個數:";
cin>>array_size;
IntArrayPtr a;
a=new int[array_size];//動態陣列
FillArray(a,array_size);
cout<<'\n'<<"快速排序開始:"<<endl;
QuickSort(a, 0, array_size-1);
cout<<"end"<<'\n';
for(int k=0;k<array_size;k++)
{
cout<<a[k]<<" ";
}
cout<<'\n';
system("pause");//getchar();
}
2)、劍指offer上一個比較好的方法,儲存了陣列的兩個位置index向前遍歷陣列,small用於儲存交換的小於軸值的數,找到一個前移一步。
#include "stdafx.h"
#include <stdlib.h>
#include <exception>
int RandomInRange(int min, int max) //隨機軸值
{
int random = rand() % (max - min + 1) + min;
return random;
}
void Swap(int* num1, int* num2)
{
int temp = *num1;
*num1 = *num2;
*num2 = temp;
}
int Partition(int data[], int length, int start, int end)
{
if(data == NULL || length <= 0 || start < 0 || end >= length)
throw new std::exception("Invalid Parameters");
int index = RandomInRange(start, end);
Swap(&data[index], &data[end]);
int small = start - 1;
for(index = start; index < end; ++ index)
{
if(data[index] < data[end])
{
++ small;
if(small != index)
Swap(&data[index], &data[small]);
}
}
++ small;
Swap(&data[small], &data[end]);
return small;
}
//遞迴快速排序
void QuickSort(int data[], int length, int start, int end)
{
if(start=end)
reurn;
int index=Partition(data, length, start, end);
if(index>start)
QuickSort(data, length, start, index-1);
if(index<end)
QuickSort(data, length, index+1.end);
}
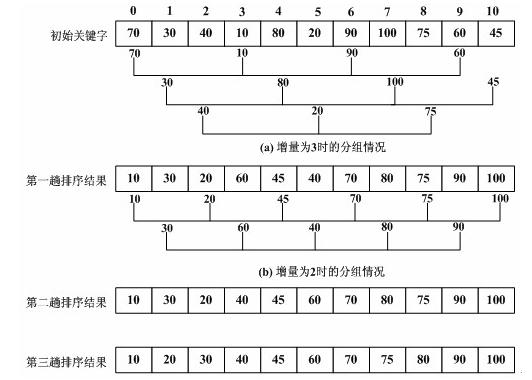
五、Shell排序(縮小增量排序)(區域性用的插入排序)
1、原理方法
由於複雜的數學原因避免使用2的冪次步長,它能降低演算法效率
子序列——每輪等數量(大到小)、等增量、等長度——插入排序——合併再重複
實現:
(1)初始增量為3,該陣列分為三組分別進行排序。(初始增量值原則上可以任意設定
(0<gap<n),沒有限制)
(2)將增量改為2,該陣列分為2組分別進行排序。
(3)將增量改為1,該陣列整體進行排序。
2、特點
1)、穩定性:不穩定
2)、時間代價——依賴於增量序列
最好 最差
平均——(約)增量除3時是O(n1.5)、O(n*logn}~O(n2)
3)、輔助儲存空間:O(1)
4)、比較
①規模非常大的資料排序不是最優選擇
②n為中等規模時是不錯的選擇
3、程式碼
#include <iostream>
using namespace std;
int a[] = {70,30,40,10,80,20,90,100,75,60,45};
void shell_sort(int a[],int n);
int main()
{
cout<<"Before Sort: ";
for(int i=0; i<11; i++)
cout<<a[i]<<" ";
cout<<endl;
shell_sort(a, 11);
cout<<"After Sort: ";
for(int i=0; i<11; i++)
cout<<a[i]<<" ";
cout<<endl;
system("pause"); //getchar();//gcc中沒有system("pause");命令
}
void shell_sort(int a[], int n)
{
for(int gap = 3; gap >0; gap--)
{
for(int i=0; i<gap; i++)
{
for(int j = i+gap; j<n; j=j+gap)
{
if(a[j]<a[j-gap])
{
int temp = a[j];
int k = j-gap;
while(k>=0&&a[k]>temp)
{
a[k+gap] = a[k];
k = k-gap;
}
a[k+gap] = temp;
}
}
}
}
}六、歸併排序
1、原理方法
分治法、歸併操作(演算法)、穩定有效的排序方法(直接插入)、等長子序列
1)、歸併操作。
設有數列{6,202,100,301,38,8,1}
初始狀態:6,202,100,301,38,8,1
第一次歸併後:{6,202},{100,301},{8,38},{1},比較次數:3;
第二次歸併後:{6,100,202,301},{1,8,38},比較次數:4;
第三次歸併後:{1,6,8,38,100,202,301},比較次數:4;
總的比較次數為:3+4+4=11,;
逆序數為14;
2)、將已有序的子序列合併,得到完全有序的序列。若將兩個有序表合併成一個有序表,稱為二路歸併。
3)、非遞迴演算法實現
假設序列共有n個元素。
①將序列每相鄰兩個數字進行歸併操作(merge),形成floor(n/2)個序列,排序後每個序列包含兩個元素
②將上述序列再次歸併,形成floor(n/4)個序列,每個序列包含四個元素
③重複上面步驟,直到所有元素排序完畢
2、特點
1)、穩定性:穩定
2)、時間代價:O(n*logn)
3)、輔助儲存空間:O(N)
4)、比較
①空間允許的情況下O(n)
②速度僅次於快速排序、n較大、有序時適用
排序:一般用於對總體無序,但是各子項相對有序的數列
求逆序對數:具體思路是,在歸併的過程中計算每個小區間的逆序對數,進而計算出大區間的逆序對數
3、程式碼
#include <iostream>
#include <ctime>
#include <cstring>
using namespace std;
void Merge(int* data, int a, int b, int length, int n)
{
int right;
if(b+length-1 >= n-1)
right = n-b;
else
right = length;
int* temp = new int[length+right];
int i = 0, j = 0;
while(i<=length-1&&j<=right-1)
{
if(data[a+i] <= data[b+j])
{
temp[i+j] = data[a+i];
i++;
}
else
{
temp[i+j] = data[b+j];
j++;
}
}
if(j == right)
{
memcpy(data+a+i+j, data+a+i,(length-i)*sizeof(int));
}
memcpy(data+a, temp, (i+j)*sizeof(int) );
delete temp;
}
void MergeSort(int* data, int n)
{
int step = 1;
while(step < n)
{
for(int i = 0; i <= n-1-step; i += 2*step)
Merge(data, i, i+step, step, n);
step *= 2;
}
}
int main()
{
int n;
cin >> n;
int *data = new int[n];
if(!data)
exit(1);
int k = n;
while(k --)
{
cin >> data[n-k-1];
}
clock_t s = clock();
MergeSort(data, n);
clock_t e = clock();
k = n;
while(k --)
{
cout << data[n-k-1] << ' ';
}
cout << endl;
cout << "the algrothem used " << e-s << " miliseconds."<< endl;
delete data;
return 0;
}七、堆排序
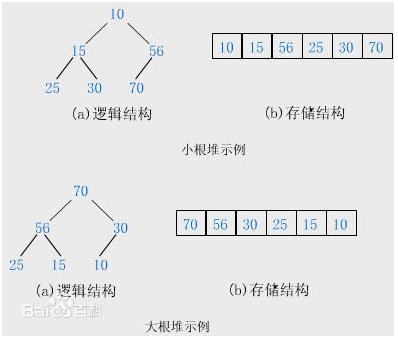
1、原理方法
BST、堆資料結構、利用陣列快速定位、無序有序區
2、特點
1)、穩定性:不穩定
2)、時間代價:O(n*logn)
3)、輔助儲存空間:O(1)
4)、比較
①常情況下速度要慢於快速排序(因為要重組堆)
②既能快速查詢、又能快速移動元素。
n較大時、關鍵字元素可能出現本身是有序時適用
3、程式碼
#include<iostream>
#include <ctime>
#include <cstring>
using namespace std;
void HeapAdjust(int array[], int i, int nLength)
{
int nChild;
int nTemp;
for (nTemp = array[i]; 2 * i + 1 < nLength; i = nChild)
{
nChild = 2 * i + 1;
if ( nChild < nLength-1 && array[nChild + 1] > array[nChild])
++nChild;
if (nTemp < array[nChild])
{
array[i] = array[nChild];
array[nChild]= nTemp;
}
else
break;
}
}
// 堆排序演算法
void HeapSort(int array[],int length)
{
int tmp;
for (int i = length / 2 - 1; i >= 0; --i)
HeapAdjust(array, i, length);
for (int i = length - 1; i > 0; --i)
{
tmp = array[i];
array[i] = array[0];
array[0] = tmp;
HeapAdjust(array, 0, i);
}
}
int main()
{
int n;
cin >> n;
int *data = new int[n];
if(!data)
exit(1);
int k = n;
while(k --)
{
cin >> data[n-k-1];
}
clock_t s = clock();
HeapSort(data, n);
clock_t e = clock();
k = n;
while(k --)
{
cout << data[n-k-1] << ' ';
}
cout << endl;
cout << "the algrothem used " << e-s << " miliseconds."<< endl;
delete data;
system("pause");
}
八、基數排序(桶排序)(屬於分配排序)
1、原理方法
基數排序(radix sort)屬於分配式排序(distribution sort)、又稱桶子法(bucket sort或bin sort)。通過鍵值的查詢,將要排序的元素分配至某些“桶”中,以達到排序的作用。
1)、分配排序(hash)
①關鍵碼確定記錄在陣列中的位置,但只能對0~n-1進行排序
②(擴充套件)允許關鍵碼重複、陣列元素可變長、每個元素成為連結串列的頭節點
③(擴充套件)允許關鍵碼範圍大於n、關鍵碼值(盒子數)比記錄數大很多時效率很差(檢查是否有元素)、同時儲存的陣列變大
④(擴充套件)桶式排序、每一個盒子與一組關鍵碼相關、桶中(較少)記錄用其它方法(收尾排序)排序
⑤堆排序
2)、LSD的基數排序
適用於位數小的數列
73, 22, 93, 43, 55, 14, 28, 65, 39, 81
①首先根據個位數的數值,在走訪數值時將它們分配至編號0到9的桶子中。
0
1 81
2 22
3 73 93 43
4 14
5 55 65
6
7
8 28
9 39
②接下來將這些桶子中的數值重新串接起來,成為以下的數列。
81, 22, 73, 93, 43, 14, 55, 65, 28, 39
接著再進行一次分配,這次是根據十位數來分配:
0
1 14
2 22 28
3 39
4 43
5 55
6 65
7 73
8 81
9 93
③接下來將這些桶子中的數值重新串接起來,成為以下的數列:
14, 22, 28, 39, 43, 55, 65, 73, 81, 93
這時候整個數列已經排序完畢;如果排序的物件有三位數以上,則持續進行以上的動作直至最高位數為止。
3)、MSD
①位數多、由高位數為基底開始進行分配
②分配之後並不馬上合併回一個陣列中,而是在每個“桶子”中建立“子桶”,將每個桶子中的數值按照下一數位的值分配到“子桶”中。在進行完最低位數的分配後再合併回單一的陣列中。
2、特點
1)、穩定性:穩定
2)、時間代價
①n個記錄、關鍵碼長度為d(趟數)、基數r(盒子數如10)、不同關鍵碼值m(堆數<=n)
②鏈式基數排序的時間複雜度為O(d(n+r))
一趟分配時間複雜度為O(n)、一趟收集時間複雜度為O(radix)、共進行d趟分配和收集
③下面是一個近似值,可自己推導
O(nlog(r)m)、O(nlogn)(關鍵碼全不同)
m<=n、d>=log(r)m
3)、輔助儲存空間
2*r個指向佇列的輔助空間、用於靜態連結串列的n個指標
4)、比較
①空間允許情況下
②適用於:
關鍵字在一個有限範圍內
有些情況下效率高於其它比較性排序法
記錄數目比關鍵碼長度大很多
調節r得到較好效能
3、程式碼
int MaxBit(int data[],int n)
{
int maxBit = 1;
int temp =10;
for(int i = 0;i < n; ++i)
{
while(data[i] >= temp)
{
temp *= 10;
++maxBit;
}
}
return maxBit;
}
//基數排序
void RadixSort(int data[],int n)
{
int maxBit = MaxBit(data,n);
int* tmpData = new int[n];
int* cnt = new int[10];
int radix = 1;
int i,j,binNum;
for(i = 1; i<= maxBit;++i)
{
for(j = 0;j < 10;++j)
cnt[j] = 0;
for(j = 0;j < n; ++j)
{
binNum = (data[j]/radix)%10;
cnt[binNum]++;
}
for(binNum=1;binNum< 10;++binNum)
cnt[binNum] = cnt[binNum-1] + cnt[binNum];
for(j = n-1;j >= 0;--j)
{
binNum= (data[j]/radix)%10;
tmpData[cnt[binNum]-1] = data[j];
cnt[binNum]--;
}
for(j = 0;j < n;++j)
data[j] = tmpData[j];
radix = radix*10;
}
delete [] tmp;
delete [] cnt;
}
轉載來自:http://m.blog.csdn.net/douyxiang/article/details/21551751
相關文章
- c++實現單連結串列C++
- MapReduce原理及簡單實現
- C++:用棧實現反轉連結串列,超簡單!C++
- C++ 手撕--基本資料結構的簡單實現C++資料結構
- vue 實現原理及簡單示例實現Vue
- C++ 引用計數技術及智慧指標的簡單實現C++指標
- LRU Cache 的簡單 C++ 實現C++
- 堆排序(實現c++)排序C++
- 堆排序c++實現排序C++
- 用go實現簡單的氣泡排序Go排序
- 歸併排序與快速排序的簡明實現及對比排序
- cJSON學習及簡單應用小結JSON
- 資料結構與演算法——基數排序簡單Java實現資料結構演算法排序Java
- Promise的使用及簡單實現Promise
- 【C++】實現一個簡單的單例模式C++單例模式
- C++的Stack模板的簡單實現C++
- 排序系統的主選單及功能實現排序
- elasticsearch實現簡單的指令碼排序(script sort)Elasticsearch指令碼排序
- 小程式簡單實現表格佈局
- 八大排序演算法python實現排序演算法Python
- 八大排序演算法實戰:思想與實現排序演算法
- 資料結構 - 單連結串列 C++ 實現資料結構C++
- 【資料結構】實現單連結串列(c++)資料結構C++
- async/await 原理及簡單實現AI
- boost bind及function的簡單實現Function
- 八大基礎排序總結排序
- 【C/C++】ghost ddl指令碼簡單實現C++指令碼
- 八大排序演算法的 Python 實現排序演算法Python
- 八大排序演算法的python實現排序演算法Python
- 選擇排序和插入排序(C++實現)排序C++
- 【練手小專案】簡易通訊錄:單連結串列實現
- 資料結構——單連結串列的C++實現資料結構C++
- 帶頭結點的單連結串列實現(C++)C++
- angular雙向繫結簡單實現Angular
- 簡單排序排序
- C++基礎簡單總結C++
- 實現一個簡單的C++協程庫C++
- Sort排序專題(5)快速排序(QuickSort)(C++實現)排序UIC++