紅黑樹移除節點
上文詳細講解了紅黑樹的概念,紅黑樹的插入及旋轉操作,根據測試程式碼建立起來的紅黑樹結構為:
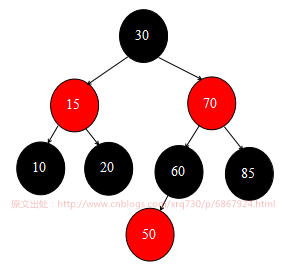
本文先研究一下紅黑樹的移除操作是如何實現的,移除操作比較複雜,具體移除的操作要進行幾次旋轉和移除的節點在紅黑樹中的位置有關,這裡也不特意按照旋轉次數選擇節點了,就找三種位置舉例演示紅黑樹移除操作如何進行:
- 移除根節點,例子就是移除節點30
- 移除中間節點,例子就是移除節點70
- 移除最底下節點,例子就是移除節點85
首先來過一下TreeMap的remove方法:
1 public V remove(Object key) { 2 Entry<K,V> p = getEntry(key); 3 if (p == null) 4 return null; 5 6 V oldValue = p.value; 7 deleteEntry(p); 8 return oldValue; 9 }
第2行的程式碼是獲取待移除的節點Entry,做法很簡單,拿key與當前節點按指定演算法做一個比較獲取cmp,cmp=0表示當前節點就是待移除的節點;cmp>0,取右子節點繼續比較;cmp<0,取左子節點繼續比較。
接著重點跟一下第7行的deleteEntry方法:
1 private void deleteEntry(Entry<K,V> p) { 2 modCount++; 3 size--; 4 5 // If strictly internal, copy successor's element to p and then make p 6 // point to successor. 7 if (p.left != null && p.right != null) { 8 Entry<K,V> s = successor(p); 9 p.key = s.key; 10 p.value = s.value; 11 p = s; 12 } // p has 2 children 13 14 // Start fixup at replacement node, if it exists. 15 Entry<K,V> replacement = (p.left != null ? p.left : p.right); 16 17 if (replacement != null) { 18 // Link replacement to parent 19 replacement.parent = p.parent; 20 if (p.parent == null) 21 root = replacement; 22 else if (p == p.parent.left) 23 p.parent.left = replacement; 24 else 25 p.parent.right = replacement; 26 27 // Null out links so they are OK to use by fixAfterDeletion. 28 p.left = p.right = p.parent = null; 29 30 // Fix replacement 31 if (p.color == BLACK) 32 fixAfterDeletion(replacement); 33 } else if (p.parent == null) { // return if we are the only node. 34 root = null; 35 } else { // No children. Use self as phantom replacement and unlink. 36 if (p.color == BLACK) 37 fixAfterDeletion(p); 38 39 if (p.parent != null) { 40 if (p == p.parent.left) 41 p.parent.left = null; 42 else if (p == p.parent.right) 43 p.parent.right = null; 44 p.parent = null; 45 } 46 } 47 }
用流程圖整理一下這裡的邏輯:
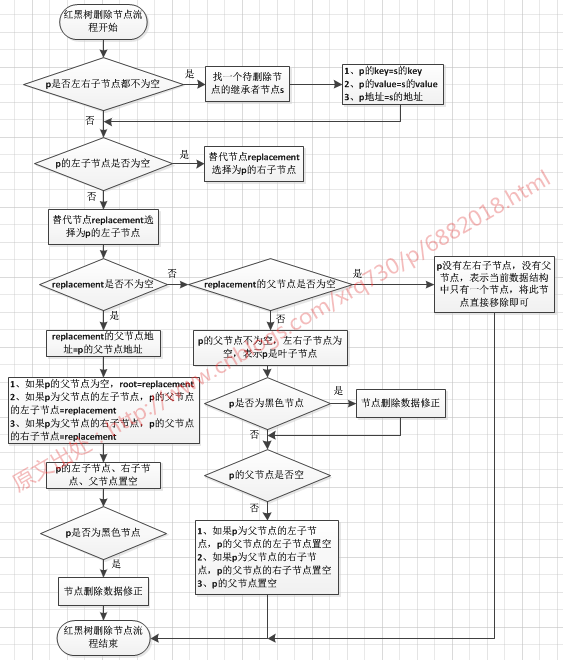
下面結合實際程式碼來看下。
移除根節點
根據上面的流程圖,根節點30左右子節點不為空,因此要先選擇繼承者,選擇繼承者的流程為:
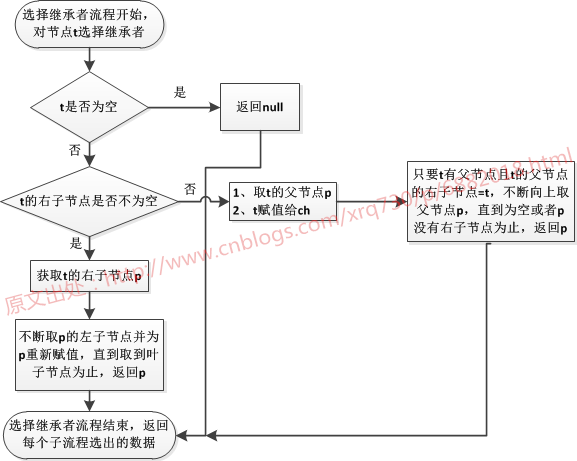
分點整理一下移除節點30做了什麼:
- 由於節點30的右子節點不為空,因此從節點70開始不斷取左子節點直到取到葉子節點為止,最終取到的節點s為節點50
- p的key=s的key即50,p的value=s的value即50,由於此時p指向的是root節點,因此root節點的key和value變化,變為50-->50
- p=s,即p原來指向的是root節點,現在p指向s節點,p與s指向同一份記憶體空間,即節點50
- 接著選擇replacement,由於p與s指向同一份記憶體空間,因此replacement判斷的是s是否有左子節點,顯然s沒有,因此replacement為空
- replacement為空,但是p有父節點,因此可以判斷出來p也就是節點50不是root節點
- 接著根據流程圖可知,節點p是一個紅色節點,這裡不需要進行移除資料修正
- 最後節點p是其父節點的左子節點,因此節點p的左子節點置為null,再將p的父節點置為null,相當於把節點p移除
經過上述流程,移除根節點30之後的資料結構如下圖:
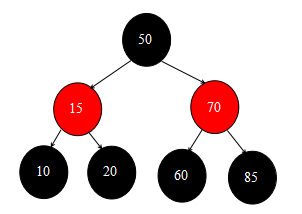
移除中間節點
接著看一下移除中間節點TreeMap是怎麼做的,這裡以移除節點70為例,繼續分點整理一下移除節點70做了什麼:
- 節點70有左右子節點,因此還是選擇繼承者,由於節點70的右子節點85沒有左子節點,因此選出來的繼承者就是節點85
- p的key=s的key即85,p的value=s的value即85,此時p指向的是節點70,因此節點70的key與value都變為85
- key與value賦值完畢後執行p=s,此時p指向節點85
- 接著選擇replacement,由於85沒有左右子節點,因此replacement為null
- replacement為null且節點p即節點85有父節點,根據流程圖可知,節點p是一個黑色節點,因此需要進行刪除資料修正
- 最後節點p是其父節點的右子節點,因此節點p的右子節點置為null,再將p的父節點置為null,相當於把節點p移除
總體流程和移除根節點差不多,唯一的區別是節點85是一個黑色節點,因此需要進行一次刪除資料修正操作。刪除資料修正實現為fixAfterDeletion方法,它的原始碼:
1 private void fixAfterDeletion(Entry<K,V> x) { 2 while (x != root && colorOf(x) == BLACK) { 3 if (x == leftOf(parentOf(x))) { 4 Entry<K,V> sib = rightOf(parentOf(x)); 5 6 if (colorOf(sib) == RED) { 7 setColor(sib, BLACK); 8 setColor(parentOf(x), RED); 9 rotateLeft(parentOf(x)); 10 sib = rightOf(parentOf(x)); 11 } 12 13 if (colorOf(leftOf(sib)) == BLACK && 14 colorOf(rightOf(sib)) == BLACK) { 15 setColor(sib, RED); 16 x = parentOf(x); 17 } else { 18 if (colorOf(rightOf(sib)) == BLACK) { 19 setColor(leftOf(sib), BLACK); 20 setColor(sib, RED); 21 rotateRight(sib); 22 sib = rightOf(parentOf(x)); 23 } 24 setColor(sib, colorOf(parentOf(x))); 25 setColor(parentOf(x), BLACK); 26 setColor(rightOf(sib), BLACK); 27 rotateLeft(parentOf(x)); 28 x = root; 29 } 30 } else { // symmetric 31 Entry<K,V> sib = leftOf(parentOf(x)); 32 33 if (colorOf(sib) == RED) { 34 setColor(sib, BLACK); 35 setColor(parentOf(x), RED); 36 rotateRight(parentOf(x)); 37 sib = leftOf(parentOf(x)); 38 } 39 40 if (colorOf(rightOf(sib)) == BLACK && 41 colorOf(leftOf(sib)) == BLACK) { 42 setColor(sib, RED); 43 x = parentOf(x); 44 } else { 45 if (colorOf(leftOf(sib)) == BLACK) { 46 setColor(rightOf(sib), BLACK); 47 setColor(sib, RED); 48 rotateLeft(sib); 49 sib = leftOf(parentOf(x)); 50 } 51 setColor(sib, colorOf(parentOf(x))); 52 setColor(parentOf(x), BLACK); 53 setColor(leftOf(sib), BLACK); 54 rotateRight(parentOf(x)); 55 x = root; 56 } 57 } 58 } 59 60 setColor(x, BLACK); 61 }
方法第3行~第30行與第30行~第57行是對稱的,因此只分析一下前半部分也就是第3行~第30行的程式碼。第三行的程式碼"x == leftOf(parentOf(x))"很顯然判斷的是x是否其父節點的左子節點。其流程圖為:
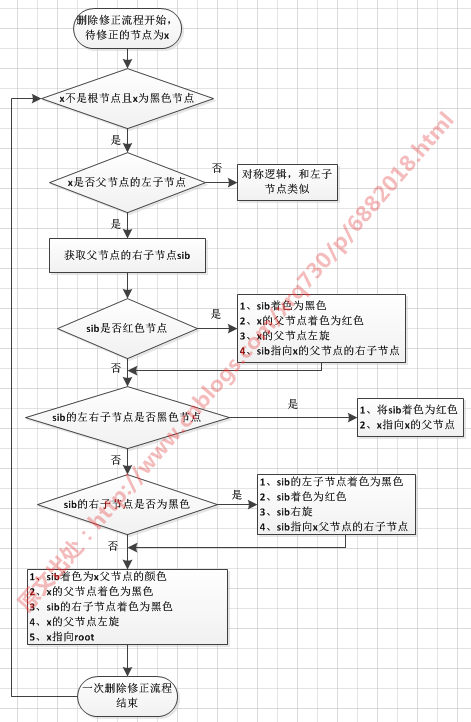
從上圖中,首先可以得出一個重要的結論:紅黑樹移除節點最多需要三次旋轉。
先看一下刪除資料修正之前的結構圖:
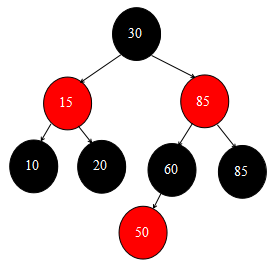
p指向右下角的黑色節點85,對此節點進行修正,上面的流程圖是p是父節點的左子節點的流程,這裡的p是父節點的右子節點,沒太大區別。
sib取父節點的左子節點即節點60,節點60是一個黑色節點,因此這裡不需要進行一次旋轉。
接著,sib的左右子節點不是黑色節點且sib的左子節點為紅色節點,因此這裡只需要進行一次旋轉的流程:
- 將sib著色為它父節點的顏色
- p的父節點著色為黑色
- sib的左子節點著色為黑色
- p的父節點右旋
經過這樣四步操作之後,紅黑樹的結構變為:
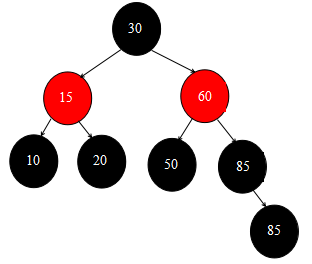
最後一步的操作在fixAfterDeletion方法的外層,節點85的父節點不為空,因此將節點85的父節點置空,最終移除節點70之後的資料結構為:

移除最底下節點
最後看看移除最底下節點的場景,以移除節點85為例,節點85根據程式碼以節點p稱呼。
節點p沒有左右子節點,因此節點p不需要進行選擇繼承者的操作;同樣的由於節點p沒有左右子節點,因此選擇出來的replacement為null。
接著由於replacement為null但是節點p是一個黑色節點,黑色節點需要進行刪除修正流程:
- 節點p是父節點的右子節點,那麼節點sib為父節點的左子節點50
- sib是黑色的,因此不需要進行一次右旋
- sib的左子節點是紅色的,因此這裡需要進行的操作是將sib著色為p父節點的顏色紅色、將p的父節點著色為黑色、將sib的左子節點著色為黑色、將p的父節點進行一次右旋
這麼做之後,樹形結構變為:
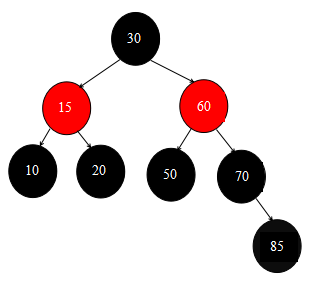
最後還是一樣,回到fixAfterDeletion方法外層的程式碼,將p的父節點置為null,即節點p就不在當前資料結構中了,完成移除,紅黑樹最終的結構為:
