注:以下的預設為2分類
1、SVM原理:
(1)輸入空間到特徵空間得對映
所謂輸入空間即是輸入樣本集合,有部分情況輸入空間與特徵空間是相同得,有一部分情況二者是不同的,而模型定義都是定義到特徵空間的,特徵空間是指所有的輸入特徵向量,特徵向量是利用數值來表示的n維向量,輸入空間到特徵空間的對映,也就是對所用的特徵進行數值量化(本人這麼理解),與概率中的隨機變數是一樣的形式,隨機變數是由樣本空間到實數集的對映,例如:拋硬幣的樣本空間是{正面,反面},對映到實數集便為{1,0}
(2)求得間隔最大化最優分離超平面
所謂分離超平面,即是能夠將所有的特徵向量劃分為兩類的平面或直線(特徵有兩個變為直線,多個變為平面,即幾維的問題),比如二維的情況下,一條線,能夠座標系中的所有點劃分為兩類,最優意為可以將所有的點儘量進行正確的劃分,間隔最大化意為:在兩類區域中各自距離直線最近的點到直線的距離是最大的,因此可以求得唯一的間隔最大化最優分離超平面w*x+b*=0,由於是距離因此是由法向量和截距決定,w*為法向量,b*為截距,此處對這個方程進行解釋:法向量是從點到平面的垂直方向,在幾何中求平面的方程時,平面方程可以設為一般方程Ax+By+Cz+D=0,這便可以看作為(A,B,C)*(x,y,z)即w*=(A,B,C),特徵向量x=(x,y,z),b*=D.同理在求直線直線可設為Ax+By+C=0,因此求超平面時即為求w*,b*.
(3)求分類決策函式
所謂分類決策函式只是一個符號函式f(x)=sign(w*x+b*),sign是一個符號函式,取輸入值的符號(正負),在上邊取得法向量和截距以後與輸入特徵向量運算後將結果帶入sign()得到分類
2、基礎概念
(1)函式間隔
上邊已經說了是求到超平面的最近距離的點的距離最大的超平面,因此求距離是很重要的一步,根據點到平面的距離公式分子為|w*x+b|,由於分母是相同的,所以|w*x+b|可以相對的表示出距離的大小。y(向量)在此表示的是每個特徵向量的分類,而由上邊已經知道,分類決策是求的符號的,因此可以確定w*x+b與y的符號(相對應元素)是相同的,因此可以利用y(w*x+b)來表示分類的正確性和確信度,這就是函式間隔: ![]()
注:超平面關於特徵空間的函式間隔是值所有特徵向量到超平面的函式間隔中的最小值

(2)幾何間隔
利用函式間隔來具體衡量時,會出現一個問題,當法向量和截距同時擴大兩倍時,超平面不變,但是函式間隔卻便為原來的兩倍,因此引入幾何間隔的概念,其實簡單的來說,幾何間隔便是函式間隔除以法向量的模,具體公式如下:
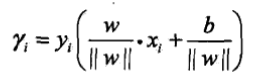
同時由超平面關於特徵空間的幾何間隔是所有特徵向量到超平面的幾何間隔中的最小值
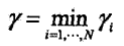
(3)支援向量
線上性可分的情況下,特徵空間中距離分離超平面的距離最近的特徵向量為支援向量
3、硬間隔最大化的求解方法
這裡解釋一下何為硬間隔最大化,這個是相對訓練資料集或說特徵空間來說的,假如資料是完全的線性可分的,則學習到的模型可以稱為硬間隔支援向量機,除此之外還有軟間隔支援向量機(近似線性可分),非線性支援向量機等,最終的目的都是為了求的w*,b*
(1)最大間隔法推導過程
根據以上的表述可以將求w*和b*歸約到兩個條件之上,首先求最大的關於特徵空間的幾何間隔,其次的約束條件為所有的幾何間隔必須都大於關於特徵空間的幾何間隔,則約束最優化問題如下:
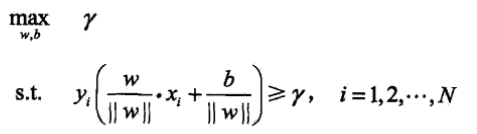
按照幾何間隔與函式間隔的關係(都是關於超平面的),這個問題又可以如下表述:

在此可以將以上的式子進行優化,上邊的第一個式子的分子(關於超平面函式間隔)會變化,而第二個式子不等號右邊的(關於超平面函式間隔)也同樣幅度變化,因此w與b也會同樣幅度的變化,因此關於超平面的函式間隔變化不會影響上述的式子,因此可以利用1來代替。此時求max(1/||w||)與min(1/2*||w||)是一樣的,一個在分母,一個在分子,至於為何會取1/2*||w||^2,求導的時候好計算1/2*2=1,如下:
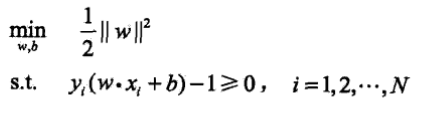
(2)學習的對偶演算法
引入拉格朗日對偶性,通過求解對偶問題得到原始問題的最優解,這樣做的優點:首先可以降低計算的難度,其次自然引入核函式(非線性可分資料的處理方式)利用拉格朗日對偶性可以構造等價對偶函式(更多請參考統計學習方法),如下:
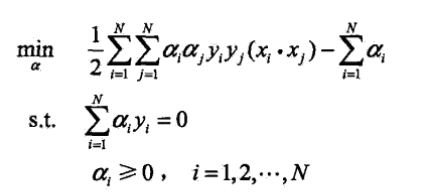
此處由定理用於求w*和b*,如下:
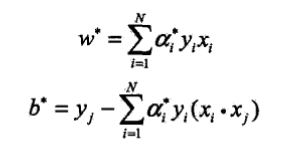
因此根據上邊的約束最優化問題即可求的拉格朗日運算元,則可求的w*與b*