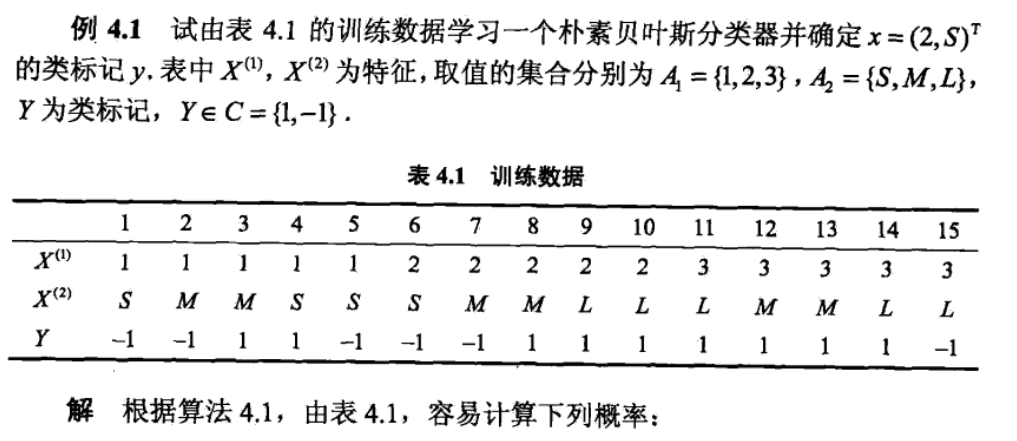
1、準備:
(1)先驗概率:根據以往經驗和分析得到的概率,也就是通常的概率,在全概率公式中表現是“由因求果”的果
(2)後驗概率:指在得到“結果”的資訊後重新修正的概率,通常為條件概率(但條件概率不全是後驗概率),在貝葉斯公式中表現為“執果求因”的因
例如:加工一批零件,甲加工60%,乙加工40%,甲有0.1的概率加工出次品,乙有0.15的概率加工出次品,求一個零件是不是次品的概率即為先驗概率,已經得知一個零件是次品,求此零件是甲或乙加工的概率是後驗概率
(3)全概率公式:設E為隨機試驗,B1,B2,....Bn為E的互不相容的隨機事件,且P(Bi)>0(i=1,2....n), B1 U B2 U....U Bn = S,若A是E的事件,則有
P(A) = P(B1)P(A|B1)+P(B2)P(A|B2)+.....+P(Bn)P(A|Bn)
(4)貝葉斯公式:設E為隨機試驗,B1,B2,....Bn為E的互不相容的隨機事件,且P(Bi)>0(i=1,2....n), B1 U B2 U....U Bn = S,E的事件A滿足P(A)>0,則有
P(Bi|A) = P(Bi)P(A|Bi)/(P(B1)P(A|B1)+P(B2)P(A|B2)+.....+P(Bn)P(A|Bn))
(5)條件概率公式:P(A|B) = P(AB)/P(B)
(6)極大似然估計:極大似然估計在機器學習中想當於經驗風險最小化,(離散分佈)一般流程:確定似然函式(樣本的聯合概率分佈),這個函式是關於所要估計的引數的函式,然後對其取對數,然後求導,在令導數等於0的情況下,求得引數的值,此值便是引數的極大似然估計
注:經驗風險:在度量一個模型的好壞,引入了損失函式,常見的損失函式有:0-1損失函式、平方損失函式、絕對損失函式、對數損失函式等,同時風險函式(期望風險)是對損失函式的期望,期望風險是關於聯合分佈的理論期望,但是理論的聯合分佈是無法求得的,只能利用樣本來估計期望,因此引入經驗風險,經驗風險就是樣本的平均損失,根據大數定理在樣本趨於無窮大的時候,這個時候經驗風險會無限趨近與期望風險
2、樸素貝葉斯演算法
(1)思路:樸素貝葉斯演算法的樸素在於對與特徵之間看作相互獨立的意思例如:輸入向量(X1, X2,....,Xn)的各個元素是相互獨立的,因此計算概率P(X1=x1,X2=x2,....Xn=xn)=P(X1=x1)P(X2=x2)......P(Xn=xn),其次基於貝葉斯定理,對於給定的訓練資料集,首先基於特徵條件獨立假設學習聯合概率分佈,然後基於此模型,對於給定的輸入向量,利用貝葉斯公式求出後驗概率最大的輸出分類標籤
(2)詳細:以判斷輸入向量x的類別的計算過程來具體說下樸素貝葉斯計算過程
<1>要計算輸入向量x的類別,即是求在x的條件下的y的概率,當y取某值最大概率,則此值便為x的分類,則概率為P(Y=ck|X=x)
<2>利用條件概率公式推導貝葉斯公式(此步非必要,本人在記貝葉斯公式時習慣這麼記)
由條件概率公式得P(Y=ck|X=x) = P(Y=ck,X=x)/P(X=x) = P(X=x | Y=ck)P(Y=ck)/P(X=x)
由全概率公式可得(替換P(X=x)):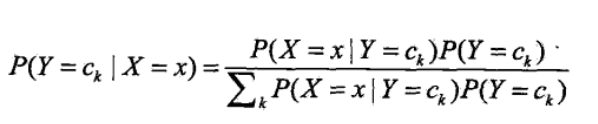
<3>由於樸素貝葉斯的“樸素”,特徵向量之間是相互獨立的,因此可得如下公式:
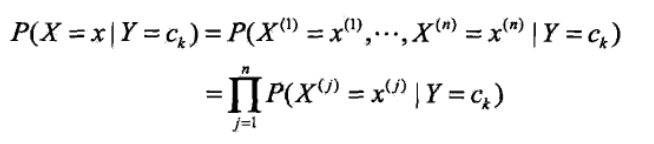
<4>將<3>中的公式帶入<2>中的貝葉斯公式可得:
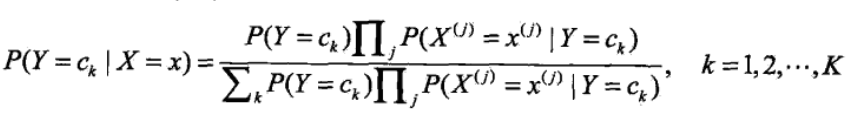
<5>看上式的分母,對於給定的輸入向量X,以及Y的所有取值,全部都用了,詳細的講即為無論是計算在向量x條件下的任意一個Y值 ck,k=1,2....K,向量和c1.....ck都用到了,因此影響P(Y=ck|X=x)大小隻有分子起作用,因此可得
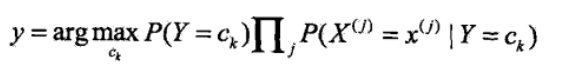
注:argmax指的是取概率最大的ck
<6>其實到<5>樸素貝葉斯的整個過程已經完畢,但是其中的P(Y=ck)和P(X(j)=x(j)|Y=ck)的求解方法並沒有說,二者得求解是根據極大似 然估計法來得其概率,即得如下公式:
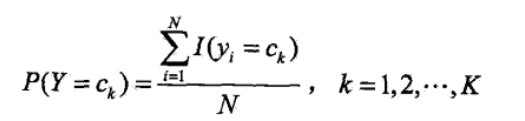
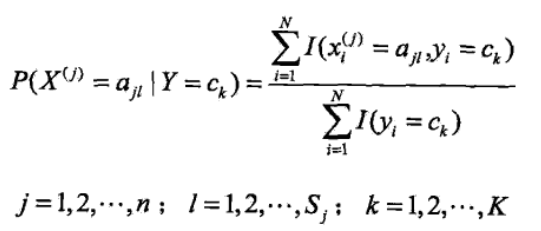
其中的I(..)是指示函式,當然這些概率在實際中可以很塊求得,可以看如下得一個題,看完之後就知道這兩個概率是怎麼求了,公式推導 過程不贅述(具體過程我也不太清楚,不過看作類似二項分佈得極大似然求值)
3、題-----一看就把上邊得串起來了(直接貼圖)