[機器學習]資訊&熵&資訊增益

關於對資訊、熵、資訊增益是資訊理論裡的概念，是對資料處理的量化，這幾個概念主要是在決策樹裡用到的概念，因為在利用特徵來分類的時候會對特徵選取順序的選擇，這幾個概念比較抽象，我也花了好長時間去理解(自己認為的理解),廢話不多說，接下來開始對這幾個概念解釋，防止自己忘記的同時，望對其他人有個借鑑的作用，如有錯誤還請指出。

1、資訊

這個是熵和資訊增益的基礎概念，我覺得對於這個概念的理解更應該把他認為是一用名稱，就比如‘雞‘(加引號意思是說這個是名稱)是用來修飾雞(沒加引號是說存在的動物即雞)，‘狗’是用來修飾狗的，但是假如在雞還未被命名為'雞'的時候，雞被命名為‘狗’，狗未被命名為‘狗’的時候，狗被命名為'雞'，那麼現在我們看到狗就會稱其為‘雞’，見到雞的話會稱其為‘雞’，同理，資訊應該是對一個抽象事物的命名，無論用不用‘資訊’來命名這種抽象事物，或者用其他名稱來命名這種抽象事物，這種抽象事物是客觀存在的。

引用夏農的話，資訊是用來消除隨機不確定性的東西，當然這句話雖然經典，但是還是很難去搞明白這種東西到底是個什麼樣，可能在不同的地方來說，指的東西又不一樣，從數學的角度來說可能更加清楚一些，數學本來就是建造在懸崖之上的一種理論，一種抽象的理論，利用抽象來解釋抽象可能更加恰當，同時也是在機器學習決策樹中用的定義，如果帶分類的事物集合可以劃分為多個類別當中，則某個類（xi）的資訊定義如下:

    　　　　　　　　　　　　　　　　　　　　　　

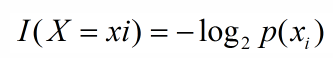
I(x)用來表示隨機變數的資訊，p(xi)指是當xi發生時的概率，這裡說一下隨機變數的概念，隨機變數時概率論中的概念，是從樣本空間到實數集的一個對映，樣本空間是指所有隨機事件發生的結果的並集，比如當你拋硬幣的時候，會發生兩個結果，正面或反面，而隨機事件在這裡可以是，硬幣是正面；硬幣是反面；兩個隨機事件，而{正面，反面}這個集合便是樣本空間，但是在數學中不會說用‘正面’、‘反面’這樣的詞語來作為數學運算的介質，而是用0表示反面，用1表示正面，而“正面->1”,"反面->0"這樣的對映便為隨機變數，即類似一個數學函式。

2、熵

既然資訊已經說完，熵說起來就不會那麼的抽象，更多的可能是概率論的定義，熵是約翰.馮.諾依曼建議使用的命名（當然是英文），最初原因是因為大家都不知道它是什麼意思，在資訊理論和概率論中熵是對隨機變數不確定性的度量,與上邊聯絡起來，熵便是資訊的期望值，可以記作：

　　　　　　　　　　　　　　　　　　　　　　　　　　

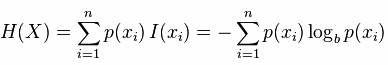
熵只依賴X的分佈，和X的取值沒有關係，熵是用來度量不確定性，當熵越大，概率說X=xi的不確定性越大，反之越小，在機器學期中分類中說，熵越大即這個類別的不確定性更大，反之越小，當隨機變數的取值為兩個時，熵隨概率的變化曲線如下圖：

　　　　　　　　　　　　　　　　　　　　

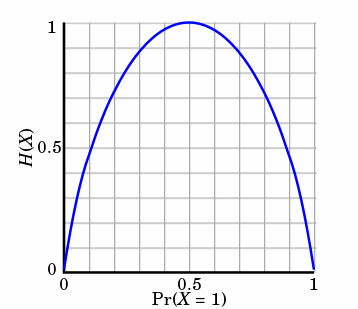
當p=0或p=1時，H(p)=0,隨機變數完全沒有不確定性，當p=0.5時，H(p)=1,此時隨機變數的不確定性最大

條件熵

條件熵是用來解釋資訊增益而引入的概念，概率定義：隨機變數X在給定條件下隨機變數Y的條件熵，對定義描述為：X給定條件下Y的條件幹率分佈的熵對X的數學期望，在機器學習中為選定某個特徵後的熵，公式如下：

　　　　　　　　　　　　　　　　

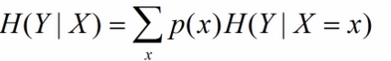
這裡可能會有疑惑，這個公式是對條件概率熵求期望，但是上邊說是選定某個特徵的熵，沒錯，是選定某個特徵的熵，因為一個特徵可以將待分類的事物集合分為多類，即一個特徵對應著多個類別，因此在此的多個分類即為X的取值。

3、資訊增益

資訊增益在決策樹演算法中是用來選擇特徵的指標，資訊增益越大，則這個特徵的選擇性越好，在概率中定義為：待分類的集合的熵和選定某個特徵的條件熵之差（這裡只的是經驗熵或經驗條件熵，由於真正的熵並不知道，是根據樣本計算出來的），公式如下：

　　　　　　　　　　　　　　　　

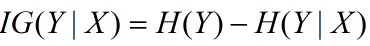
注意：這裡不要理解偏差，因為上邊說了熵是類別的，但是在這裡又說是集合的熵，沒區別，因為在計算熵的時候是根據各個類別對應的值求期望來等到熵

4、資訊增益演算法（舉例，摘自統計學習演算法）

訓練資料集合D，|D|為樣本容量，即樣本的個數（D中元素個數），設有K個類Ck來表示，|Ck|為Ci的樣本個數，|Ck|之和為|D|，k=1，2.....，根據特徵A將D劃分為n個子集D1，D2.....Dn，|Di|為Di的樣本個數，|Di|之和為|D|,i=1,2,....,記Di中屬於Ck的樣本集合為Dik,即交集，|Dik|為Dik的樣本個數，演算法如下：

輸入：D，A

輸出：資訊增益g(D,A)

(1)D的經驗熵H(D)

　　　　　　　　

 

此處的概率計算是根據古典概率計算，由於訓練資料集總個數為|D|，某個分類的個數為|Ck|，在某個分類的概率，或說隨機變數取某值的概率為：|Ck|/|D|

(2)選定A的經驗條件熵H(D|A)

　　　　　　　　

 

此處的概率計算同上，由於|Di|是選定特徵的某個分類的樣本個數，則|Di|/|D|,可以說為在選定特徵某個分類的概率，後邊的求和可以理解為在選定特徵的某個類別下的條件概率的熵，即訓練集為Di，交集Dik可以理解在Di條件下某個分類的樣本個數，即k為某個分類，就是縮小訓練集為Di的熵

(3)資訊增益