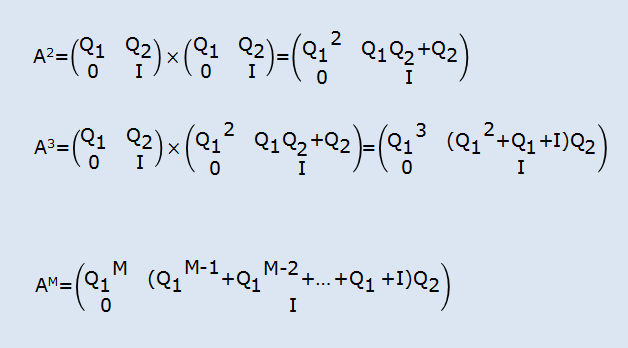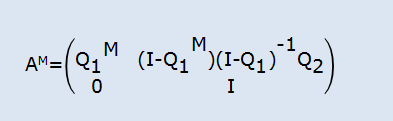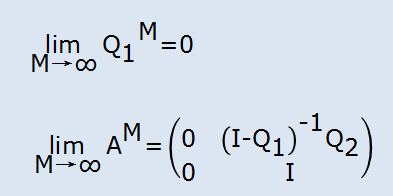演算法題——投籃比賽獲勝概率問題

問題描述：

甲乙兩人比賽投籃。約定甲先投籃，每人投籃投進一球，則繼續投球，若投失一球，則換人投球。初始積分為1分，甲每投進一球，積分加1分；乙每投進1球，積分減1分。若積分達到N分（N＞1），甲獲勝；若積分減至0分，乙獲勝。假定甲投進的概率為P₁（0＜P₁＜1），乙投進的概率為P₂（0＜P₂＜1）。那麼這場投籃比賽，甲獲勝的概率P為多少？

 

 

很顯然的，甲獲勝的概率P是和P₁、P₂、N相關的。

P₁越大，P越大

P₂越大，P越小

N越大，P越小

 

不失一般性，假設P₁=0.7，P₂=0.3，N=4，求甲獲勝的概率P

 

解法一：大數量模擬法（10000000次）

 

在前文 演算法題——投籃比賽獲勝的概率 中介紹的就是這種方法。

用計算機模擬10000000次比賽的過程，統計甲獲勝的次數。然後甲獲勝的次數比上總次數接近甲獲勝的概率。

一共模擬了10批次的比賽，每批次模擬10000000次比賽的過程（P₁=0.7，P₂=0.3，N=4）

第1批次，甲獲勝8282467次

第2批次，甲獲勝8282839次

第3批次，甲獲勝8283808次

第4批次，甲獲勝8281636次

第5批次，甲獲勝8282652次

第6批次，甲獲勝8283432次

第7批次，甲獲勝8281948次

第8批次，甲獲勝8284125次

第9批次，甲獲勝8284626次

第10批次，甲獲勝8283720次

 

平均10個批次，平均甲獲勝8283125次。那麼甲獲勝的概率大約是82.83125%

 

 

解法二：矩陣法

 

解法一是建立在大量的模擬上，所得的資料離理論值還是有一定的偏差的（模擬的次數越多，偏差值越小）。那麼，本方法就是從理論上來計算甲獲勝的概率P的。

 

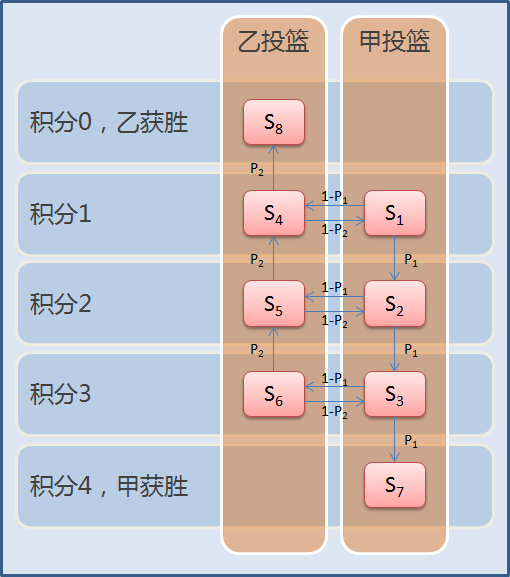
分析該問題，可以得出整個問題存在8個狀態（狀態的個數和N有關，狀態的個數為2N個）

分別是

積分0分，乙獲勝

積分1分，乙要投籃；積分1分，甲要投籃

積分2分，乙要投籃；積分2分，甲要投籃

積分3分，乙要投籃；積分3分，甲要投籃

積分4分，甲獲勝

 

這8個狀態之間的關係可以用下圖表示（為了後文表述方便，給這8個狀態起了名字，分別是S₁、S₂、S₃、……、S₇、S₈）

 

如圖，比賽初始是在S₁狀態，比賽結束在S₇（甲獲勝）或S₈（乙獲勝）狀態，狀態之間有轉換箭頭。

例如：當前是S₃狀態（積分3，甲投籃），那麼下一個狀態可能是S₆（甲投失，換成積分3，乙投籃的狀態）或者是S₇（甲投進，積分4，甲獲勝的狀態）。再比如當前是S₆狀態（積分3，乙投籃），那麼下一個狀態可能是S₅（乙投進，換成積分2，乙投籃的狀態）或者是S₃（乙投失，換成積分3，甲投籃的狀態）

 

 

用A₁、A₂、A₃、A₄、A₅、A₆、A₇、A₈表示某次投籃後，各個狀態所佔的比重。那麼再投籃一次後，各個狀態的所佔比重計算如下（等號左邊是新的比重，等號右邊是原來的比重）：

A₁=A₄（1-P₂）

A₂=A₁P₁+A₅（1-P₂）

A₃=A₂P₁+A₆（1-P₂）

A₄=A₅P₂+A₁（1-P₁）

A₅=A₆P₂+A₂（1-P₁）

A₆=A₃（1-P₁）

A₇=A₃P₁+A₇

A₈=A₄P₂+A₈

 

可以把上面的計算式子轉換為矩陣的形式

令向量T_i=（A₁、A₂、A₃、A₄、A₅、A₆、A₇、A₈）表示第i次（i=0時表示初始狀態）投籃各狀態所佔比重的向量，則

T_i+1=T_i×A

 

其中，A為8*8的矩陣，如下圖所示

 

因為

T₁=T₀×A

T₂=T₁×A=T₀×A×A=T₀×A²

T₃=T₂×A=T₀×A²×A=T₀×A³

……

T_M=T₀×A^M

 

實際上，本題中的甲獲勝的概率就是當M趨向於無窮時，T_M的A₇分量。同時，T_M的A₈分量表示乙獲勝的概率

把上面的矩陣A分成四個小矩陣Q₁、Q₂、Q₃、Q₄，如下圖所示：

 

 

 

由於T_M=T₀×A^M，故在這兒分析A^M

 

 

 

由於矩陣I-Q₁可逆，則上述的表示式可以簡化為

Q₁^M-1+Q₁^M-2+…+Q₁+I=（Q₁^M-1+Q₁^M-2+…+Q₁+I）（I-Q₁）（I-Q₁）^-1

=（Q₁^M-1+Q₁^M-2+…+Q₁+I-Q₁^M-Q₁^M-1-…-Q₁）（I-Q₁）^-1

=（I-Q₁^M）（I-Q₁）^-1

 

 

於是矩陣A^M就簡化成如下形式

 

 

對於矩陣Q₁來說。由於是非負矩陣，根據G. Frobenius可知，它的譜半徑ρ滿足不等式，r≤ρ≤R。其中r表示G₁矩陣中所有行和值（一行所有元素加起來的值）的最小值，R表示G₁矩陣中所有行和值最大值。可知R=1，r=MIN（1-P₁，1-P₂）

 

而在李華所著的《非負矩陣譜半徑的一個新估計》中，將譜半徑的範圍縮小

 

得到如下的不等式

r≤ρ≤R-（1-P₂）（R-r）/R

 

由此可以得知Q₁的譜半徑ρ＜1

而利用譜半徑的性質可知，當譜半徑ρ＜1時，矩陣Q₁的M次方趨向於0矩陣

 

於是本問題就得出了結論，令T為T_M中M趨向無窮大時的向量，A^*為A^M中M趨向無窮大時的矩陣。可知

 

T=T₀×A^*

 

 

本題中P₁=0.7，P₂=0.3，T₀=（1，0，0，0，0，0，0，0）

 

矩陣A和矩陣A*分別為

 

於是

T=T₀×A*=（0，0，0，0，0，0，0.828302342，0.171697658）

 

甲獲勝的概率是82.8302342%，乙獲勝的概率是17.1697658%

 

和方法一的結論比較（82.83125%），還是非常接近的。也間接說明了方法一的可行性。

 

 

本方法從理論的角度給出了問題的解。本示例中，P₁=0.7，P₂=0.3，N=4

本方法的計算難點就是求（I-Q₁）^-1，這是一個消耗大量計算時間的過程。Q₁是一個2N-2*2N-2的稀疏矩陣，I-Q₁也是一個2N-2*2N-2的稀疏矩陣，求它的逆矩陣是非常耗時的

 

 

可以在本方法的理論基礎上，給出簡化的計算方法，也就是接下來講的迭代法

 

解法三：迭代法

迭代法的理論基礎在解法二上

依次計算向量T₁、T₂、……、T_M等等

若T_M+1-T_M≈0（若每個分量小於10^-9，我們就認為兩個向量相等），

 

還是以上面的示例為例（P₁=0.7，P₂=0.3，N=4）

 

T₁=（0，0.7，0，0.3，0，0，0，0）

T₂=（0.21，0，0.49，0，0.21，0，0，0.09）

T₃=（0，0.294，0，0.126，0，0.147，0.343，0.09）

T₄=（0.0882，0，0.3087，0，0.1323，0，0.343，0.1278）

T₅=（0，0.15435，0，0.06615，0，0.09261，0.55909，0.1278）

T₆=（0.046305，0，0.172872，0，0.074088，0，0.55909，0.147645）

T₇=（0，0.0842751，0，0.0361179，0，0.0518616，0.6801004，0.147645）

T₈=（0.02528253，0，0.09529569，0，0.04084101，0，0.6801004，0.15848037）

T₉=（0，0.046286478，0，0.019837062，0，0.028588707，0.746807383，0.15848037）

T₁₀=（0.013885943，0，0.05241263，0，0.022462556，0，0.746807383，0.164431489）

T₁₁=（0，0.025443949，0，0.01090455，0，0.015723789，0.783496224，0.164431489）

T₁₂=（0.007633185，0，0.028817417，0，0.012350321，0，0.783496224，0.167702854）

T₁₃=（0，0.013988454，0，0.005995052，0，0.008645225，0.803668415，0.167702854）

T₁₄=（0.004196536，0，0.015843576，0，0.006790104，0，0.803668415，0.169501369）

……

T₇₁=（0，4.08706E-10，0，1.7516E-10，0，2.52594E-10，0.828302342，0.171697657）

T₇₂=（1.22612E-10，0，4.6291E-10，0，1.9839E-10，0，0.828302342，0.171697658）

 

T72≈T71，故可以認為T=（0，0，0，0，0，0，0.828302342，0.171697658）

 

也就是甲獲勝的概率是82.8302342%，乙獲勝的概率是17.1697658%

 

本方法相比解法二，計算上來得簡單，僅僅通過迭代計算（加加乘乘），就計算出最後的結果。相比求矩陣的逆來說，要簡單的多。