Codeforces 500B. New Year Permutation[連通性]

Candy?發表於2016-09-17
B. New Year Permutation
time limit per test
2 seconds
memory limit per test
256 megabytes
input
standard input
output
standard output

User ainta has a permutation p1, p2, ..., pn. As the New Year is coming, he wants to make his permutation as pretty as possible.

Permutation a1, a2, ..., an is prettier than permutation b1, b2, ..., bn, if and only if there exists an integer k (1 ≤ k ≤ n) where a1 = b1, a2 = b2, ..., ak - 1 = bk - 1 and ak < bk all holds.

As known, permutation p is so sensitive that it could be only modified by swapping two distinct elements. But swapping two elements is harder than you think. Given an n × n binary matrix A, user ainta can swap the values of pi and pj (1 ≤ i, j ≤ n, i ≠ j) if and only if Ai, j = 1.

Given the permutation p and the matrix A, user ainta wants to know the prettiest permutation that he can obtain.

Input

The first line contains an integer n (1 ≤ n ≤ 300) — the size of the permutation p.

The second line contains n space-separated integers p1, p2, ..., pn — the permutation p that user ainta has. Each integer between 1 and n occurs exactly once in the given permutation.

Next n lines describe the matrix A. The i-th line contains n characters '0' or '1' and describes the i-th row of A. The j-th character of the i-th line Ai, j is the element on the intersection of the i-th row and the j-th column of A. It is guaranteed that, for all integers i, j where 1 ≤ i < j ≤ n, Ai, j = Aj, i holds. Also, for all integers i where 1 ≤ i ≤ n, Ai, i = 0 holds.

Output

In the first and only line, print n space-separated integers, describing the prettiest permutation that can be obtained.

Examples
input
7
5 2 4 3 6 7 1
0001001
0000000
0000010
1000001
0000000
0010000
1001000
output
1 2 4 3 6 7 5
input
5
4 2 1 5 3
00100
00011
10010
01101
01010
output
1 2 3 4 5
Note

In the first sample, the swap needed to obtain the prettiest permutation is: (p1, p7).

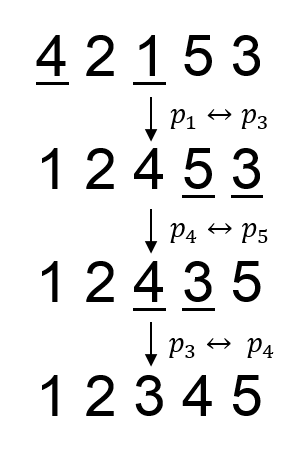
In the second sample, the swaps needed to obtain the prettiest permutation is (p1, p3), (p4, p5), (p3, p4). 

A permutation p is a sequence of integers p1, p2, ..., pn, consisting of n distinct positive integers, each of them doesn't exceed n. The i-th element of the permutation p is denoted as pi. The size of the permutation p is denoted as n.

 

位置的swap關係可以構成一個連通塊

每一個連通塊貪心就行了

實現上，可以用並查集維護，然後對於1到n每一個位置找連通塊中最小的

 

//
//  main.cpp
//  cf500b
//
//  Created by Candy on 9/16/16.
//  Copyright © 2016 Candy. All rights reserved.
//

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int N=305;
int n,p[N],a[N][N],ans[N];
char tmp[N];
int fa[N];
int find(int x){return x==fa[x]?x:fa[x]=find(fa[x]);}
int main(int argc, const char * argv[]) {
    scanf("%d",&n);
    for(int i=1;i<=n;i++) scanf("%d",&p[i]),fa[i]=i;
    for(int i=1;i<=n;i++){
        scanf("%s",tmp+1);
        for(int j=1;j<=n;j++)
            if(tmp[j]=='1'){
                int x=find(i),y=find(j);
                if(x!=y) fa[y]=x;
            }
    }
    for(int i=1;i<=n;i++){
        int mn=i;
        for(int j=i+1;j<=n;j++)
            if(find(i)==find(j)&&p[j]<p[mn]) mn=j;
        swap(p[mn],p[i]);
        printf("%d ",p[i]);
    }
    return 0;
}

 

 

 

相關文章