各類聚類（clustering）演算法初探

Andrew.Hann發表於2018-01-20
聚類演算法

1. 聚類簡介

0x1：聚類是什麼？

聚類是一種運用廣泛的探索性資料分析技術，人們對資料產生的第一直覺往往是通過對資料進行有意義的分組。很自然，首先要弄清楚聚類是什麼？

直觀上講，聚類是將物件進行分組的一項任務，使相似的物件歸為一類，不相似的物件歸為不同類

但是，要達到這個目的存在幾個很困難的問題

1. 上述提及的兩個目標在很多情況下是互相沖突的。從數學上講，雖然聚類共享具有等價關係甚至傳遞關係，但是相似性（或距離）不具有傳遞關係。具體而言，假定有一物件序列，X1，....，Xm，所有相鄰元素（Xi-1、Xi+1）兩兩都非常相似，但是X1和Xm非常不相似。這種情況常常發生在cluster超過一定尺寸的時候，元素之間的傳遞性假設在這些場景下不一定100%符合真實規律。
2. 另一個基本問題是聚類缺乏實際情況，這是無監督學習的共同問題。聚類是一種無監督學習，即我們不能預測label，因此對於聚類，我們沒有明確的成功評估過程。
另一方面，對於一個給定的物件集合，可以有多種有意義的劃分方式，這可能是因為物件間的距離（或相似性）有多種隱式的定義，例如將演講者的錄音根據演講者的口音聚類或根據內容聚類。所以，給定一個資料集，有多種不同的聚類解決方案

0x2：聚類的公理化描述

對於各種各樣的聚類演算法，有沒有一些基本性質是獨立於具體演算法或任務的呢？很多人嘗試對聚類提出一個公理化的定義，讓我們討論Kleninberg（2003）提出的嘗試方法：

考慮一個聚類函式F，將任意有限域X及不相似函式d作為輸入，返回X的一個劃分

1. 尺度不變性是一種非常自然的要求，如果聚類函式輸出的結果依賴於測量點之間的距離測度單位，那將顯得十分奇怪。
2. 豐富性要求主要想說明聚類函式的輸出是由函式d全權決定，也是一種非常直觀的特性。
3. 一致性要求是和聚類基本定義相關的要求，即我們希望相似的點聚到一類，不相似的點分屬不同類，因此共享同類的點更相似，已經分離的點不相似，聚類函式應當對之前的聚類決策有很強的“支撐”作用

值得注意的是，Kleinberg在2003已經給出了下述“不可能”結論！

不存在一個函式F同時滿足上述三種屬性：尺度不變性，豐富性，一致性。

但是，Kleninberg的“不可能”結論可以通過改變屬性的限制範圍來規避。即不用100%滿足上述三條件

例如，如果討論含固定數量引數的聚類函式，很自然地將豐富性改為 k-豐富性（即，將域劃分到k個子集，這個限制比豐富性RI原則更鬆散一些）。k-均值聚類滿足k-豐富性、尺度不變性和一致性，因此能夠達到一致。或者可以放鬆一致性屬性

這反過來告訴我們。給定一項任務，聚類函式的選取必須考慮該任務的特定屬性（是否可以放鬆要求，又是否有一些地方是需要強要求）。沒有統一的聚類解決方案，就像沒有一種分類演算法能夠對每一項可學習任務都能學習（no free lunch定理）。和其他分類預測一樣，聚類必須考慮特定任務的先驗知識

0x3：資料探勘對聚類的典型泛化要求

不同的演算法有著不同的應用背景，有的適合大資料集，可以發現任意形狀的聚類；有的演算法思想簡單直觀，適用於小資料集。總的來說，演算法都試圖從不同途徑實現對資料集進行高效、可靠的聚類。資料探勘對聚類的典型要求包括：

1. 可伸縮性：

當聚類物件由幾百上升到幾百萬，我們希望最後的聚類結果的準確度能保持一致

2. 處理不同型別屬性的能力：

有些聚類演算法，其處理物件的屬性的資料型別只能是數值型別，但是在實際應用場景中，我們往往會遇到其他型別的資料（例如二後設資料），分類資料等等，雖然我們也可以在預處理資料時將這些其他型別的資料轉換成數值型資料，但是在聚類效率上或者聚類準確度上往往會有折損

3. 發現任意形狀的類簇：

因為許多聚類演算法是基於距離（例如歐式距離或曼哈頓距離）來量化例項物件之間的相似度的，基於這種方式，我們往往只能發現相似尺寸和密度的球狀類簇或者凸形類簇。但是在很多場景下，類簇的形狀可能是任意的

4. 對聚類演算法初始化引數的知識需求的最小化：

很多演算法在分析過程中需要開發者提供一定的引數（例如期望的類簇K個數、類簇初始質心），這導致了聚類結果對這些引數是十分敏感的，這不僅加重了開發者的負擔，也非常影響聚類結果的準確性

5. 處理噪聲資料的能力：

所謂的噪聲資料，可以理解為影響聚類結果的干擾資料，這些噪聲資料的存在會造成聚類結果的“畸變”，最終導致低質量的聚類

6. 增量聚類和對輸入次序的不敏感：

一些聚類演算法不能將新加入的資料插入到已有的聚類結果，輸入次序的敏感是指，對於給定的資料物件集合，以不同的次序提供輸入物件時，最終產生的聚類結果的差異會比較大

7. 高維性：

有些演算法只適合處理2維或者3維的資料，而對高維資料的處理能力很弱，因為在高維空間中資料的分佈可能十分稀疏，而且高度傾斜。

8. 基於約束的聚類：

在實際應用中可能需要在各種條件下進行聚類，因為同一個聚類演算法，在不同的應用場景中所帶來的聚類結果也是各異的，因此找到滿足“特定約束”的具有良好聚類特性的資料分組是十分有挑戰的。這裡最困難的問題就在於如何是識別我們要解決的問題中隱含的“特定約束”具體是什麼，以及該使用什麼演算法來最好的“適配”這種約束

9. 可解釋性和可用性：

我麼希望得到的聚類結果都能用特定的語義、知識進行解釋，和實際的應用場景相聯絡

0x4：聚類的大致分類

聚類是將資料物件的集合分成相似的物件類的過程。使得同一個簇（或類）中的物件之間具有較高的相似性，而不同簇中的物件具有較高的相異性。按照聚類的尺度，聚類方法可被分為以下三種

1. 基於距離的聚類演算法: 基於距離的聚類演算法是用各式各樣的距離來衡量資料物件之間的相似度
2. 基於密度的聚類方法: 基於密度的聚類演算法主要是依據合適的密度函式等
3. 基於互連性的聚類演算法: 基於互連性的聚類演算法通常基於圖或超圖模型，將高度連通的物件聚為一類

0x5：資訊瓶頸 - 關於聚類的更一般化的原理討論

資訊瓶頸是由 Tishby，Pereira和 Bialek 提出的聚類技術，其概念來源於資訊理論。

用一個文字聚類的問題來解釋這個概念，假設我們將每個文字表示為一個詞袋，即，每個文件都是一個向量，其中 n 是字典的長度，當且僅當第 i 個詞在文件中出現。給定一個有 m 個文件的集合，我們可以將 m 個文件的詞袋錶示理解為隨機變數 x 的聯合概率分佈，指示文件的身份，以及一個隨機變數 y，指示單詞在詞典中的身份。

根據這種解釋，資訊瓶頸是指：將聚類屬性表示為另一個隨機變數C（歸納到具體的類別 k 中）（其中 k 同樣由方法確定）。一旦將 x，y，C 表述為隨機變數，我們可以使用資訊理論中的方法來表示聚類目標。資訊瓶頸的目標是：

其中是兩個隨機變數的互資訊，在每個點分屬聚類的所有可能概率分佈中求取極小值。

直觀上講，我們希望達到兩個矛盾的目標。

1）一方面，我們希望文件屬性和聚類屬性的互資訊儘可能小，這反映了我們希望對原始資料進行強壓縮。

2）另一方面，我們希望聚類變數和詞屬性的互資訊儘可能大，這反映了保留文件資訊（用詞在文件中出現來表示）的目標。將引數統計中的最小充分統計量推廣到了任意分佈。

解資訊瓶頸準則下的最優化問題通常是非常困難的，解決方案思路上類似EM準則

0x6：聚類的進階觀點

我們這個小節來討論一些抽象的概念，例如聚類是什麼？聚類演算法和輸入一個空間輸出一個空間分佈的任意函式的區別是什麼？聚類有沒有一些基本性質是獨立於具體演算法或任務的。

回答這些問題的一種方式是公理化方法，考慮一個聚類函式 F，將任意有限域 X 及不相似函式 d 作為輸入，返回 X 的一個劃分，考慮這類函式的三種特性：

1. 尺度不變性（SI）

對任意的域集 X，不相似函式 d，以及任意的 a > 0，下式成立：

尺度不變性是一種非常自然的要求，因為如果聚類函式輸出的結果依賴於測量點之間的距離測度單元，那將顯得十分奇怪和不合理。

2. 豐富性（Ri）

對任意的有限集 X 和劃分 C = （C1，C2，....，Ck)（劃分到非空子集），存在多種不相似函式 d 使得 。

豐富性要求主要想說明聚類函式的輸出是由函式 d 全權決定，也是一種十分直觀的特徵。

3. 一致性（Co）

如果 d 和 d' 都是 X 上的不相似函式，對任一，根據 F（X，d）：

如果 x，y 屬於同一類，則。

如果 x，y 屬於不同類，則

那麼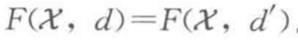

一致性要求是和聚類基本定義相關的要求，我們希望相似的點聚到一類，不相似的點分屬不同類，因此共享同類的點更相似，已經分離的點不相似，聚類函式應當對之前的聚類決策有很強的“支撐”作用。

給定一項任務，聚類函式的選取必須考慮該任務的特定屬性，沒有同意的聚類解決方案，就像沒有一種分類演算法能夠對每一項可學習任務都能學習（沒有免費的午餐定理）。

和其他分類預測一樣，聚類必須考慮特定任務的先驗知識。

Relevant Link:

《深入理解機器學習 - 從原理到演算法》
http://blog.csdn.net/itplus/article/details/10087581
http://www.sohu.com/a/193777221_473283

 

1. K-Means演算法(K-means clustering K均值聚類演算法) - 基於劃分的聚類

0x1：K-means演算法模型

一種流行的聚類演算法是首先對可能的聚類定義一個代價函式，聚類演算法的目標是尋找一種使代價最小的劃分。

在這類範例中，聚類任務轉化為一個優化問題，目標函式是一個從輸入（X，d）和聚類方案 C = （C1，C2，....，Ck）對映到正實數（即損失值）的函式。

給定這樣一個目標函式，我們將其表示為 G，對於給定的一個輸入（X，d），聚類演算法的目標被定義為尋找一種聚類 C 使 G（（X，d），C）最小。

其中，Ci 中心點被定義為：

所以上式也可以寫成如下形式：

為了達到上述目標，需要執行一些合適的搜尋演算法。

但是要注意的是，理論和實際的工程化是存在一定的差距的。k均值目標函式在實際的聚類應用中很常見。然而，事實證明尋找k均值（k-means）演算法的最優解通常是計算不可行的（NP問題，甚至接近常數近似解的求解是NP問題）。所以通常會用下面這種簡單的迭代演算法作為替代演算法

因此，多數情況下，k均值聚類值得是這種演算法的結果而不是最小化 k 均值目標函式的結果

需要注意的是，k均值演算法的目標函式優化過程是單調非增的（也就是每次的迭代至少不會讓結果更糟），但是 k均值演算法本身對達到收斂的迭代次數並沒有給出理論保證。

此外，演算法給出的 k均值目標函式輸出值和目標函式的最小可能值之差，並沒有平凡下界，實際上，k均值可能會收斂到區域性最小值。為了提高 k均值的結果，通常使用不同的隨機初始化中心點，將該程式執行多次，並選取最優的結果。

除此之外，有一些無監督的演算法可以作為 k均值演算法的前置演算法，用來選取初始化中心。

0x2：K-means演算法過程

kMeans聚類演算法是資料探勘十大演算法之一，演算法需要接受引數 k（k 個初始聚類中心）(也可由演算法隨機產生指定)，即將資料集進行聚類的數目和k個簇的初始聚類“中心”，結果是同一類簇中的物件相似度最高，不同類簇中的資料相似度最低，其聚類過程可以用下圖表示

如圖所示，資料樣本用圓點表示，每個簇的中心點用叉叉表示

1. 聚類中心個數K

聚類中心的個數K需要事先給定，但在實際中這個 K 值的選定是非常難以估計的，很多時候，事先並不知道給定的資料集應該分成多少個類別才最合適。這個過程會是一個漫長的除錯過程，我們通過設定一個[k, k+n]範圍的K類值，然後逐個觀察聚類結果，最終決定該使用什麼K值對當前資料集是最佳的

在實際情況中，往往是對特定的資料集有對應一個最佳的K值，而換一個資料集，可能原來的K值效果就會下降。但是同一個專案中的一類資料，總體上來說，通過一個抽樣小資料集確定一個最佳K值後，對之後的所有K值都能獲得較好的效果

2. 初始聚類中心(質心)的選擇

剛開始時是原始資料，雜亂無章，沒有label，看起來都一樣，都是綠色的

Kmeans需要人為地確定初始聚類中心，不同的初始聚類中心可能導致完全不同的聚類結果。在實際使用中我們往往不知道我們的待聚類樣本中哪些是我們關注的label，人工事先指定質心基本上是不現實的，在大多數情況下我們採取隨機產生聚類質心這種策略

假設資料集可以分為兩類，令K = 2，隨機在座標上選兩個點，作為兩個類的中心點(聚類質心)

3. 確定了本輪迭代的質心後，將餘下的樣本點根據距離度量標準進行歸類

這一步也非常直觀，計算樣本點和所有質心的“距離”，選取“距離”最小（argmin）的那個質心作為該樣本所屬的類別。

這裡要注意的是，特徵空間中兩個例項點的距離是兩個例項點相似程度的反映，高維向量空間點的距離求解，可以泛化為Lp距離公式，它在不同的階次數中分為不同的形式

p = 1：Manhattan Distance距離(曼哈頓距離)：

p = 2：Euclidean Distance距離(尤拉距離)：

p = λ( 3 <= λ <= 正無窮 ) - Lp距離

p = 正無窮：距離等於各個座標點的最大值

為了幫助理解，下圖展示了二維空間中p取不同值時，與原點的Lp距離為1(Lp = 1)的點的圖形

4. 演算法收斂（終止/停機）條件是什麼？

我們前面說過，計算K-means問題的目標函式最優解是一個NP問題，我們大多數時候都是針對聚類結果施加一些約束，得到一個終止/停止條件，例如一種比較常用的停止條件：

這樣不斷進行"劃分—更新—劃分—更新"，直到每個簇的中心不在移動為止

0x3：Kmeans演算法步驟圖示描述

1. 步驟一 - 選取質心

在輸入資料集裡面隨機選擇三個向量作為初始中心點（下圖中的紅綠藍三個圓點），這裡的K值為3, 也就是一開始從資料集裡面選擇了三個向量，這算作第一次迭代

2. 步驟二 - 距離聚類

將每個向量分配到離各自最近的中心點，從而將資料集分成了K個類

3. 步驟三 - 重選新質心

計算得到上步得到聚類中每一聚類觀測值的均值作為新的質心。這裡體現的思想是這樣的：因為我們是無監督學習，對於待分類的樣本叢集我們沒有任何的先驗知識，完全不知道該怎麼分類，那麼我們就暴力地、勇敢地、隨機地踏出第一步，然後不斷地去修正我們的分類器，不得不說，這和人生的很多的做人做事的道理是類似的

4. 步驟四（人生就是一個勇敢踏出第一步，然後不斷自我否定和修正成長的過程）

重複步驟三，直至結果收斂，這裡的收斂是指所有點到各自中心點的距離的和收斂

用sklearn python 對2維資料點進行kMeans聚類 

# -*- coding: utf-8 -*-

from sklearn.cluster import KMeans
import numpy as np

if __name__ == '__main__':
    X = np.array([
        [1, 2], [1, 4], [1, 0],
        [4, 2], [4, 4], [4, 0]
    ])
    kmeans = KMeans(n_clusters=2, random_state=0).fit(X)
    print kmeans.labels_

    kmeans.predict([[0, 0], [4, 4]])

    print kmeans.cluster_centers_

kMeans這種無監督聚類進行一次無監督聚類後，也可以得到一個分類器(classifier)，它是對當前train set的一個特徵空間劃分，基於這個分類器可以用於之後對新樣本點的分類預測，這種就是有監督聚類

0x4：不同K值、不同的初始化中心點方式對Kmeans分類效果的影響

我們知道，K-mean的3大核心要素是：K值、距離度量公式、初始質心的選擇。我們這個小節用一小程式碼來討論下這些值是如何影響演算法的分類效果

# -*- coding: utf-8 -*-

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D


from sklearn.cluster import KMeans
from sklearn import datasets

if __name__ == '__main__':
    np.random.seed(5)

    centers = [[1, 1], [-1, -1], [1, -1]]
    iris = datasets.load_iris()
    X = iris.data
    y = iris.target

    estimators = {'k_means_iris_3': KMeans(n_clusters=3),
                  'k_means_iris_8': KMeans(n_clusters=8),
                  'k_means_iris_bad_init': KMeans(n_clusters=3, n_init=1, init='random')}

    fignum = 1
    for name, est in estimators.items():
        fig = plt.figure(fignum, figsize=(4, 3))
        plt.clf()
        ax = Axes3D(fig, rect=[0, 0, .95, 1], elev=48, azim=134)

        plt.cla()
        est.fit(X)
        labels = est.labels_

        ax.scatter(X[:, 3], X[:, 0], X[:, 2], c=labels.astype(np.float))

        ax.w_xaxis.set_ticklabels([])
        ax.w_yaxis.set_ticklabels([])
        ax.w_zaxis.set_ticklabels([])
        ax.set_xlabel('Petal width')
        ax.set_ylabel('Sepal length')
        ax.set_zlabel('Petal length')
        fignum = fignum + 1

    # Plot the ground truth
    fig = plt.figure(fignum, figsize=(4, 3))
    plt.clf()
    ax = Axes3D(fig, rect=[0, 0, .95, 1], elev=48, azim=134)

    plt.cla()

    for name, label in [('Setosa', 0),
                        ('Versicolour', 1),
                        ('Virginica', 2)]:
        ax.text3D(X[y == label, 3].mean(),
                  X[y == label, 0].mean() + 1.5,
                  X[y == label, 2].mean(), name,
                  horizontalalignment='center',
                  bbox=dict(alpha=.5, edgecolor='w', facecolor='w'))
    # Reorder the labels to have colors matching the cluster results
    y = np.choose(y, [1, 2, 0]).astype(np.float)
    ax.scatter(X[:, 3], X[:, 0], X[:, 2], c=y)

    ax.w_xaxis.set_ticklabels([])
    ax.w_yaxis.set_ticklabels([])
    ax.w_zaxis.set_ticklabels([])
    ax.set_xlabel('Petal width')
    ax.set_ylabel('Sepal length')
    ax.set_zlabel('Petal length')
    plt.show()

可以看到，Kmeans這種無監督學習的演算法並不能保證聚類出來的"族群"是有"實際意義"的，即Kmeans得到的分類族群可能只是在歐式空間上相近的點集，但是實際上它們並不一定真的就屬於同一個類別。另外一方面，Kmeans的分類結果和K值有強關聯，如果我們傳入了一個"不合理"的K值，有可能導致Kmeans的過擬合，最後得到一個"錯誤"的分類結果

在思考的深層次一些，這其實和Kleinberg對聚類演算法的公理化定義有關，標準的聚類公理化定義是需要滿足豐富性（Ri）原則的，但是這個條件太強了，所以k-means是一個滿足k-豐富性原則的演算法，k-豐富性原則是一個弱約束，不同的k值下，產生的分類結果也自然是不同的

0x5：K-means在影象處理上的應用

1. Color Quantization(真彩色降維低彩色) using K-Means

這個例子要求做的是從96615真彩色"降維"到64種色彩，這裡我個人理解聚類和降維的本質有共通的地方，聚類的目標是把相似的資料集歸納到同一個類別裡，如果歸納完之後直接用這個新的類別代表該類別所有的樣本集，那這個聚類就是一次降維過程。同樣，回到這個例子，如果我們對一副真彩色的高維度畫素的影象進行相似畫素色聚類，本質上就是把原始影象降維成了一個低緯度低彩色圖

# -*- coding: utf-8 -*-

import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.metrics import pairwise_distances_argmin
from sklearn.datasets import load_sample_image
from sklearn.utils import shuffle
from time import time

if __name__ == '__main__':
    n_colors = 64

    # Load the Summer Palace photo
    china = load_sample_image("china.jpg")

    # Convert to floats instead of the default 8 bits integer coding. Dividing by
    # 255 is important so that plt.imshow behaves works well on float data (need to
    # be in the range [0-1])
    china = np.array(china, dtype=np.float64) / 255

    # Load Image and transform to a 2D numpy array.
    w, h, d = original_shape = tuple(china.shape)
    assert d == 3
    image_array = np.reshape(china, (w * h, d))

    # 用1000張影象來訓練出一個Kmeans分類器
    print("Fitting model on a small sub-sample of the data")
    t0 = time()
    image_array_sample = shuffle(image_array, random_state=0)[:1000]
    kmeans = KMeans(n_clusters=n_colors, random_state=0).fit(image_array_sample)
    print("done in %0.3fs." % (time() - t0))

    # 用訓練好的Kmeans分類器對本例中的"夏宮"影象進行聚類處理，實際上就是在降維
    # Get labels for all points
    print("Predicting color indices on the full image (k-means)")
    t0 = time()
    labels = kmeans.predict(image_array)
    print("done in %0.3fs." % (time() - t0))

    codebook_random = shuffle(image_array, random_state=0)[:n_colors + 1]
    print("Predicting color indices on the full image (random)")
    t0 = time()
    labels_random = pairwise_distances_argmin(codebook_random,
                                              image_array,
                                              axis=0)
    print("done in %0.3fs." % (time() - t0))


    def recreate_image(codebook, labels, w, h):
        """Recreate the (compressed) image from the code book & labels"""
        d = codebook.shape[1]
        image = np.zeros((w, h, d))
        label_idx = 0
        for i in range(w):
            for j in range(h):
                image[i][j] = codebook[labels[label_idx]]
                label_idx += 1
        return image


    # Display all results, alongside original image
    plt.figure(1)
    plt.clf()
    ax = plt.axes([0, 0, 1, 1])
    plt.axis('off')
    plt.title('Original image (96,615 colors)')
    plt.imshow(china)

    plt.figure(2)
    plt.clf()
    ax = plt.axes([0, 0, 1, 1])
    plt.axis('off')
    plt.title('Quantized image (64 colors, K-Means)')
    plt.imshow(recreate_image(kmeans.cluster_centers_, labels, w, h))

    plt.figure(3)
    plt.clf()
    ax = plt.axes([0, 0, 1, 1])
    plt.axis('off')
    plt.title('Quantized image (64 colors, Random)')
    plt.imshow(recreate_image(codebook_random, labels_random, w, h))
    plt.show()

把原始影象的96615畫素點聚類為64畫素點，中間的影象就是Kmeans聚類後的結果，可以看到，從肉眼視覺角度看，影象並沒有明顯地失真

0x6：從混合模型和EM演算法的角度來談kmeans聚類

實際上，混合模型和EM演算法又是另一塊非常龐大的主題，我們這裡不深入討論，只討論kmeans更高層次的抽象概括，混合模型除了提供一個構建更復雜的概率分佈的框架之外，混合模型也可以用於資料聚類。本質上來說，K均值演算法對應於用於高斯混合模型的EM演算法的一個特定的非概率極限

1. 用形式化方式描述Kmeasn

引入一組 D 維向量，其中，，且是與第 k 個聚類關聯的一個代表。我們可以認為表示了聚類的中心，我們的目標是找到所有資料點分別屬於的聚類，以及一組向量，使得每個資料點和它最近的向量之間的距離的平方和最小。對於每個資料點，我們引入一組對應的二值指示變數，其中，表示資料點屬於 K 個聚類中的哪一個（指示函式）

有了以上定義，之後我們可以定義一個目標函式，也被稱為失真度量（distortion measure）

（公式9.1）

它表示每個資料點與它被分配的向量之間的距離的平方和。我們的目標是找到和的值，使得 J 達到最小值。我們可以用一種迭代的方法完成這件事，其中每次迭代涉及到兩個連續的步驟，分別對應

1. 的最優化（E期望）：首先，我們為選擇一些初始值。然後在第一階段，我們保持固定，關於最小化 J

2. 的最優化（M最大化）：在第二階段，我們保持固定，關於最小化 J。不斷重複這2個階段優化直到收斂

我們看到，在EM步驟中，每次都是固定其中一個變數，求另一個變數的極值，避免直接對二元變數直接求極值的計算困難問題。為了說明這一點，我們在K均值演算法中使用 E步驟和 M步驟的說法

首先考慮最優化，公式（9.1）給出的 J 是的一個線性函式，因此最優化過程可以很容易地進行，得到一個解析解。與不同的 n 相關的項是獨立的，因此我們可以對每個 n 分別進行最優化，只要 k 的值使最小，我們就令等於1。換句話說，我們可以簡單地將資料點的聚類設定為最近的聚類中心，更形式化地，這可以表達為：（1-of-k）

現在考慮固定時，關於的最優化。目標函式 J 是的一個二次函式，令它關於的導數等於零，即可達到最小值，即

求導結果為：，這個表示式的分母等於單個聚類 k 中資料點的數量，因此這個結果有一個非常簡單直觀的含義，即令等於單個類別 k 的所有資料點的均值

上述兩個步驟合起來稱為K均值（K-means）演算法

重新為資料點分配聚類的步驟以及重新計算聚類均值的步驟重複進行，直到聚類的分配不改變（或者直到迭代次數超過了某個最大值）。由於每個階段都減小了目標函式 J 的值，因此演算法的收斂性得到了保證，但是要注意的是，演算法可能收斂到 J 的一個區域性最小值而不是全域性最小值 

Relevant Link:

http://blog.itpub.net/12199764/viewspace-1479320/
https://blog.yueyu.io/p/1614
http://scikit-learn.org/stable/modules/generated/sklearn.cluster.KMeans.html
http://scikit-learn.org/stable/auto_examples/cluster/plot_cluster_iris.html#sphx-glr-auto-examples-cluster-plot-cluster-iris-py
http://scikit-learn.org/stable/auto_examples/cluster/plot_color_quantization.html#sphx-glr-auto-examples-cluster-plot-color-quantization-py
http://scikit-learn.org/stable/auto_examples/cluster/plot_face_compress.html#sphx-glr-auto-examples-cluster-plot-face-compress-py 
http://blog.csdn.net/gamer_gyt/article/details/51244850
http://scikit-learn.org/stable/auto_examples/cluster/plot_kmeans_assumptions.html#sphx-glr-auto-examples-cluster-plot-kmeans-assumptions-py
http://scikit-learn.org/stable/auto_examples/cluster/plot_kmeans_digits.html#sphx-glr-auto-examples-cluster-plot-kmeans-digits-py
http://chunqiu.blog.ustc.edu.cn/?p=435#comment-3556
http://f.dataguru.cn/thread-639729-1-1.html
http://www.cnblogs.com/bourneli/p/3645049.html 
http://www.cnblogs.com/bourneli/p/3645049.html
https://en.wikipedia.org/wiki/Silhouette_(clustering)
https://kapilddatascience.wordpress.com/2015/11/10/using-silhouette-analysis-for-selecting-the-number-of-cluster-for-k-means-clustering/
http://scikit-learn.org/stable/auto_examples/cluster/plot_kmeans_silhouette_analysis.html#sphx-glr-auto-examples-cluster-plot-kmeans-silhouette-analysis-py
http://scikit-learn.org/stable/auto_examples/cluster/plot_kmeans_stability_low_dim_dense.html#sphx-glr-auto-examples-cluster-plot-kmeans-stability-low-dim-dense-py
http://scikit-learn.org/stable/modules/clustering.html#mini-batch-kmeans
http://scikit-learn.org/stable/auto_examples/cluster/plot_mini_batch_kmeans.html#sphx-glr-auto-examples-cluster-plot-mini-batch-kmeans-py
http://scikit-learn.org/stable/auto_examples/text/document_clustering.html#sphx-glr-auto-examples-text-document-clustering-py
http://coolshell.cn/articles/7779.htm

 

2. K-Means++演算法

0x1：從爬山法問題中切入談kmeans的缺陷以及kmeans++緩解了什麼問題

假設我們的目標是到達山頂，我們採用的演算法如下

1. 從山上的某個隨機位置出發開始
2. Repeast
3. 每次都都沿著“更高”的方向走一步
4. Until直到某一步發現無論往任何方向走都不會更高

這個演算法看起來十分合理，但是我們考慮下面這個圖上執行上述演算法

我們如何從A點出發，只會到達B點而不會到達最高頂點D點，即我們到達的是區域性最優點而不是全域性最優點。

k-means演算法和上面的爬山法類似，不能保證最後能夠找到最優的劃分簇。這是因為演算法一開始選擇的是隨機質心，基於隨機質心，演算法只能找到區域性最優化分簇（例如影象的B點）

可以看到，對於kmeans這種EM過程來說，最終的聚類結果嚴重依賴於初始中心點的選擇。

K-Means主要有兩個最重大的缺陷 - 都和初始值有關

1. K是事先給定的，這個K值的選定是非常難以估計的。很多時候，事先並不知道給定的資料集應該分成多少個類別才最合適 
2. K-Means演算法需要用初始隨機種子點來搞，這個隨機種子點太重要，不同的隨機種子點會有得到完全不同的結果

但是k-means++演算法從一定程度上解決了該問題，k-means++選擇初始seeds的基本思想就是：初始的聚類中心之間的相互距離要儘可能的遠

0x2：k-Means++演算法步驟

1. 從輸入的資料點集合中隨機選擇一個點作為第一個種子點(聚類中心)
2. 對於資料集中的每一個點x，計算它與最近聚類中心(指已選擇的聚類中心)的距離D(x)並儲存在一個陣列裡，然後把這些距離加起來得到Sum(D(x))
3. 選擇一個新的資料點作為新的聚類中心，選擇的原則是: D(x)較大的點被選取作為聚類中心的概率較大(kMeans不同類別的距離越遠越好)
    1) 先取一個能落在Sum(D(x))中的隨機值Random
    2) 然後用Random -= D(x)，直到其結果 <= 0
    3) 選取在這個"遞減過程"中D(x)最大的點，此時的點就是下一個"種子點"
4. 重複2和3直到k個聚類中心被選出來
5. 利用這k個初始的聚類中心來執行標準的k-means演算法

可以看到演算法的第三步選取新中心的方法，這樣就能保證距離D（x）較大的點，會被選出來作為聚類中心了。

同時k-measn這裡並不直接用“hard方式”通過遍歷每次選取D（x）最大的值作為下一個中心點，而是引入了隨機過程，通過隨機過程，柔和地體現了：

以正比於D（x）的概率（概率由距離決定）隨機選擇一個資料點作為新的中心點

以一段python程式碼模擬該過程。假設由包含資料點及其權重的元祖構成列表。roulette函式會基於隨機過程以正比於某個資料點的權重的概率來選擇點。

#-*- coding:utf-8 -*-

import collections
import random
random.seed()

def roulette(datalist):
    i = 0
    soFar = datalist[0][1]
    ball = random.random()
    while soFar < ball:
        i += 1
        soFar += datalist[i][1]
    return datalist[i][0]


if __name__ == "__main__":
    data = [
        ("dp1", 0.25),
        ("dp2", 0.4),
        ("dp3", 0.1),
        ("dp4", 0.15),
        ("dp5", 0.1)
    ]
    results = collections.defaultdict(int)
    for i in range(1000):
        results[roulette(data)] += 1
    print results

我們可以看到，在1000次選擇中，函式按照正比於權重的方式柔和地進行了點的選擇

0x3：Kmeans++演算法策略

k-means++聚類的基本思想就是：雖然第一個中心點仍然隨機選擇，但其他的點則優先選擇那些彼此相距很遠的點

Relevant Link:

http://www.csdn.net/article/2012-07-03/2807073-k-means

 

3. 基於連結的聚類演算法 - 基於分層的聚類（自底向上）

這種型別的聚類方法不需要指定最終聚成的簇的數目（例如K值）。取而代之的是，演算法一開始將每個例項都看成一個簇，然後在演算法的每次迭代中都將最相似的兩個簇合並在一起，該過程不斷重複直到只剩下一個簇為止。該方法稱為層次聚類。演算法最終終止於單個簇，該簇由兩個子簇構成，而其中的每個子簇又由兩個更小的子簇構成，如此遞迴迴圈下去

基於連結的聚類演算法可能是最簡單直觀的聚類形式。這類演算法需要一系列迴圈，從一些瑣碎的聚類開始，將每個資料點作為一個單點聚類，然後，這類演算法不斷迴圈將前一階段中“最近”的兩個聚類合併。因此，聚類數目隨著迴圈過程逐漸減少，如果一直進行下去，這類演算法會將所有定義域資料點歸為一個大類

為了將該類演算法定義清楚，需要確定兩個引數：

1. 我們需要決定怎樣測量（或定義）類間距離
2. 我們需要確定什麼時候終止合併

0x1：連結聚類模型

我們前面說了，對這類連結聚類（自下而上聚類）有兩個非常關鍵的因素就是距離度量和終止條件，它們共同決定了連結聚類演算法的演算法模型

1. 域子集間距離度量公式

1.1 單連結聚類（single-linkage clustering）：類間距離定義為兩類元素間的最短距離（取兩兩組合最短距離的那個）。在單連結聚類中，如果簇A到簇B的距離要比簇C到簇B的距離更近，則會將A和B先合併成一個新簇。

1.2 最大連結聚類：類間距定義為兩類元素間的最大距離（取兩兩組合最長距離的那個）。

1.3 平均連結聚類（average-linkage clustering）：類間距離定義為兩類元素之間距離的平均值。

2. 合併終止條件

基於連結的聚類演算法是凝聚式的，一開始，資料完全是碎片化的，然後逐步構建越來越大的聚類，如果我們沒有加入停止規則，連結演算法的結果可以用聚類系統樹圖來描述，即，一個域子集構成的樹，其葉子節點是單元素集，根節點為全域。例如下圖所示：

常用的停止準則包括：

1. 固定類的數量：固定引數 k，當聚類數目為 k 時停止聚類。
使用這種停止準則需要我們對我們的場景要有較強的領域知識，即預先知道需要聚類的數量

2. 設定距離上限：設定域子集間距最大上限，如果在某一輪迭代中，所有的元件距離都超過該閾值，則停止聚類
使用這種停止準則，實際上隱含了一種假設，即相似的樣本在特徵空間上距離很近，且聚集在一個較小的區域內，彼此之間距離較近。而不同類別的樣本在族群上彼此會拉開距離。
所以通過設定一定的距離上限，可以在對一個族群聚集完畢後及時收斂停止，開啟新族群的聚集

0x2：單連結/平均連結/最大連結聚類效果對比

# -*- coding:utf-8 -*-

from time import time

import numpy as np
from scipy import ndimage
from matplotlib import pyplot as plt

from sklearn import manifold, datasets

digits = datasets.load_digits(n_class=10)
X = digits.data
y = digits.target
n_samples, n_features = X.shape

np.random.seed(0)

def nudge_images(X, y):
    # Having a larger dataset shows more clearly the behavior of the
    # methods, but we multiply the size of the dataset only by 2, as the
    # cost of the hierarchical clustering methods are strongly
    # super-linear in n_samples
    shift = lambda x: ndimage.shift(x.reshape((8, 8)),
                                  .3 * np.random.normal(size=2),
                                  mode='constant',
                                  ).ravel()
    X = np.concatenate([X, np.apply_along_axis(shift, 1, X)])
    Y = np.concatenate([y, y], axis=0)
    return X, Y


X, y = nudge_images(X, y)


#----------------------------------------------------------------------
# Visualize the clustering
def plot_clustering(X_red, X, labels, title=None):
    x_min, x_max = np.min(X_red, axis=0), np.max(X_red, axis=0)
    X_red = (X_red - x_min) / (x_max - x_min)

    plt.figure(figsize=(6, 4))
    for i in range(X_red.shape[0]):
        plt.text(X_red[i, 0], X_red[i, 1], str(y[i]),
                 color=plt.cm.spectral(labels[i] / 10.),
                 fontdict={'weight': 'bold', 'size': 9})

    plt.xticks([])
    plt.yticks([])
    if title is not None:
        plt.title(title, size=17)
    plt.axis('off')
    plt.tight_layout()

#----------------------------------------------------------------------
# 2D embedding of the digits dataset
print("Computing embedding")
X_red = manifold.SpectralEmbedding(n_components=2).fit_transform(X)
print("Done.")

from sklearn.cluster import AgglomerativeClustering

for linkage in ('ward', 'average', 'complete'):
    clustering = AgglomerativeClustering(linkage=linkage, n_clusters=10)
    t0 = time()
    clustering.fit(X_red)
    print("%s : %.2fs" % (linkage, time() - t0))

    plot_clustering(X_red, X, clustering.labels_, "%s linkage" % linkage)


plt.show()

單純就這個數字聚類的場景來看，平均連結聚類的效果最好

0x3：連結演算法模型

決定連結演算法具體形式的最重要的因素就是“域間相似性度量函式”，因此可分為單連結、平均連結、最大連結 這3種。

1. 單連結聚類演算法

單連結演算法和 Kruskal 演算法很相似，目的是在加權圖上找到一個最小生成樹。

從圖的視角來看單連結演算法的演算法執行過程，圖的頂點是 X 中的元素，邊（x，y）的權重是距離 d（x，y）。每次單連結演算法將兩個聚類進行合併，相當於在一顆樹中新增一條邊。

單連結演算法得到的邊集合和最小生成樹是一致的。

2. 平均連結聚類演算法

3. 最大連結聚類演算法

Relevant Link:

http://scikit-learn.org/stable/auto_examples/cluster/plot_digits_linkage.html#sphx-glr-auto-examples-cluster-plot-digits-linkage-py
http://scikit-learn.org/stable/modules/clustering.html#hierarchical-clustering

 

4. DBSCAN（Density-Based Spatial Clustering of Application with Noise） - 基於密度的聚類演算法

基於密度的聚類方法與其他方法的一個根本區別是：它不是基於各種各樣的距離度量的，而是基於密度的。因此它能克服基於距離的演算法只能發現“類圓形”的聚類的缺點。DBSCAN的指導思想是：

用一個點的∈鄰域內的鄰居點數衡量該點所在空間的密度，只要一個區域中的點的密度大過某個閾值，就把它加到與之相近的聚類中去

它可以找出形狀不規則（oddly-shaped）的cluster，且聚類時不需要事先知道cluster的個數

0x1：DBSCAN模型

考慮資料集合，首先引入以下概念與數學記號：

1. ∈鄰域（∈ neighborhood）

設，稱為 x 的∈鄰域。顯然，

2. 密度（density）

設，稱為 x 的密度。注意，這裡的密度是一個整數值，且依賴於半徑∈

3. 核心點（core point）

設，若（核心點閾值 minimum numberof points required to form a cluster），則稱 x 為 X 的核心點。記由 X 中所有核心點構成的集合為，並記表示由 X 中的所有非核心點構成的集合

4. 邊界點（border point）

若滿足。即 x 的∈鄰域中存在核心點，則稱 x 為 X 的邊界點。記由 X 中所有邊界點構成的集合為

此外，邊界點也可以這麼定義，若，且 x 落在某個核心點的∈鄰域內，則稱 x 為 X 的一個邊界點。一個邊界點可能同時落入一個或多個核心點的∈鄰域

5. 噪音點（noise point）

記，則稱 x 為噪音點

直觀上來說，核心點對應稠密區域內部的點，邊界點對應稠密區域邊緣的點，而噪音點對應稀疏區域中的點。如下圖所示：

需要注意的是，核心點位於簇的內部，它確定無誤地屬於某個特定的簇；噪音點是資料集中的干擾資料，它不屬於任何一個簇；而邊界點是一類特殊的點，它位於一個或幾個簇的邊緣地帶，它可能屬於一個簇，也可能屬於另外一個簇，其簇歸屬並不明確

6. 直接密度可達（directly density-reachable）

設，則稱 y 是從 x 直接密度可達的

7. 密度可達（density-reachable）

設，若它們滿足直接密度可達的，，則稱是從密度可達的

值得注意的是，當 m = 2時，密度可達即為直接密度可達。密度可達是直接密度可達的一種推廣。事實上，密度可達是直接密度可達的傳遞閉包。

8. 密度相連（density-connected）

設，若 y 和 z 均是從 x 密度可達的，則稱 y 和 z 是密度相連的。顯然，密度相連具有對稱性。

9. 類（cluster）

稱非空集合是 X 的一個類（cluster），如果它滿足：對於

（1）Maximality：若，且 y 是從 x 密度可達的，則

（2）Connectivity：若，則 x，y 是密度相連的

0x2：DBSCAN演算法過程

DBSCAN演算法的核心思想如下：從某個選定的核心點出發，不斷向密度可達的區域擴張，從而得到一個包含核心點和邊界點的最大化區域，區域中任意亮點密度相連

考慮資料集合。DBSCAN演算法的目標是將資料集合 X 分成 K 個cluster（k由演算法自動推斷得到，無需事先指定）及噪音點組成，為此，引入cluster標記陣列

由此，DBSCAN演算法的目標就是生成標記陣列，而 K 即為中互異的非負數的個數

輸入：樣本集D=(x1,x2,...,xm)，鄰域引數(ϵ,MinPts), 樣本距離度量方式

輸出： 簇劃分C.　

可以看到，DBSCAN在不斷髮現新的核心點的同時，還通過直接密度可達，發現核心點鄰域內的核心點，並把這些鄰域內的核心點都歸納到第 k 個聚類中。而噪音點沒每輪 k 聚類中會被全域性過濾不會參與下一輪啟發式發現中，只有邊界點在下一次跌打中會被再次嘗試檢驗是否能夠成為新聚類的核心點

0x3：hello world！DBSCAN

# -*- coding:utf-8 -*-

import numpy as np

from sklearn.cluster import DBSCAN
from sklearn import metrics
from sklearn.datasets.samples_generator import make_blobs
from sklearn.preprocessing import StandardScaler


# #############################################################################
# Generate sample data
centers = [[1, 1], [-1, -1], [1, -1]]
X, labels_true = make_blobs(n_samples=750, centers=centers, cluster_std=0.4,
                            random_state=0)

X = StandardScaler().fit_transform(X)

# #############################################################################
# Compute DBSCAN
db = DBSCAN(eps=0.3, min_samples=10).fit(X)
print db.labels_
core_samples_mask = np.zeros_like(db.labels_, dtype=bool)
print core_samples_mask
core_samples_mask[db.core_sample_indices_] = True
labels = db.labels_

# Number of clusters in labels, ignoring noise if present.
n_clusters_ = len(set(labels)) - (1 if -1 in labels else 0)

print('Estimated number of clusters: %d' % n_clusters_)
print("Homogeneity: %0.3f" % metrics.homogeneity_score(labels_true, labels))
print("Completeness: %0.3f" % metrics.completeness_score(labels_true, labels))
print("V-measure: %0.3f" % metrics.v_measure_score(labels_true, labels))
print("Adjusted Rand Index: %0.3f"
      % metrics.adjusted_rand_score(labels_true, labels))
print("Adjusted Mutual Information: %0.3f"
      % metrics.adjusted_mutual_info_score(labels_true, labels))
print("Silhouette Coefficient: %0.3f"
      % metrics.silhouette_score(X, labels))

# #############################################################################
# Plot result
import matplotlib.pyplot as plt

# Black removed and is used for noise instead.
unique_labels = set(labels)
colors = [plt.cm.Spectral(each)
          for each in np.linspace(0, 1, len(unique_labels))]
for k, col in zip(unique_labels, colors):
    if k == -1:
        # Black used for noise.
        col = [0, 0, 0, 1]

    class_member_mask = (labels == k)

    xy = X[class_member_mask & core_samples_mask]
    plt.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor=tuple(col),
             markeredgecolor='k', markersize=14)

    xy = X[class_member_mask & ~core_samples_mask]
    plt.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor=tuple(col),
             markeredgecolor='k', markersize=6)

plt.title('Estimated number of clusters: %d' % n_clusters_)
plt.show()

Relevant Link: 

http://shiyanjun.cn/archives/1288.html
https://en.wikipedia.org/wiki/DBSCAN 
https://www.cnblogs.com/hdu-2010/p/4621258.html
http://blog.csdn.net/itplus/article/details/10088625
https://www.cnblogs.com/pinard/p/6208966.html
http://blog.csdn.net/xieruopeng/article/details/53675906
http://www.cnblogs.com/aijianiula/p/4339960.html
http://scikit-learn.org/stable/modules/generated/sklearn.cluster.DBSCAN.html

 

5. Clustering by fast search and find of density peaks（CFSFDP聚類）- 基於密度（Density）的聚類

該演算法是Alex Rodriguez和Alessandro Laio在Science上發表的《Clustering by fast search and find of density peaks》所提出的一種新型的基於密度的聚類演算法。

0x1：演算法思想

該聚類演算法的核心思想在於對聚類中心（cluster centers）的刻畫上，演算法認為聚類中心同時具有以下兩個特點：

1. 聚類中心本身密度大，即它被密度均不超過它的鄰居包圍，或者說聚類中心是整個簇中密度最大的點；
2. 聚類中心與其他密度更大的資料點之間的“距離”相對更大；

0x2：演算法模型

該演算法的假設類簇（cluster centers）的中心由一些區域性密度比較低的點圍繞，並且這些點距離其他有高區域性密度的點的距離都比較大。

對於樣本集中的任何資料點s，可以定義兩個值：區域性密度ρi以及到高區域性密度點的距離δi，這兩個值僅僅取決於兩點之間的距離dij。

1. 區域性密度ρi

包括 Cut-off kernel 和 Gaussian kernel 兩種計算方式：

1）Cut-off kernel：階躍統計函式，只關注資料點是否在dc閾值範圍內

，其中函式，

引數稱為截斷距離（cutoff distance），需要在演算法啟動時顯式指定。
從該模型公式中可以看出，區域性密度 ρi 表示的是樣本集 S 中與資料點 xi 之間的的距離小於 dc 的資料點。

這裡 dc 可以理解為一個邊界閾值，dc 設定的越小，表示希望演算法對聚類的敏感度越高，即在儘可能小的區域內發現聚類社群。

2）Gaussian kerne：柔性距離統計函式

和 cut-off kernel一樣，與 x 的距離小於 dc 的資料點越多，pi 的值越大。

對比上面兩式可以看出，cut-off kernel為離散值，Gaussian kernel為連續值，因此，相對來說，Gaussian產生衝突（即不同的資料點具有相同的區域性密度值）的概率更小

2. 到高區域性密度點的距離δi

設表示資料點區域性密度的一個降序排列下標序，即它滿足：。

則可以定義：

這個公式非常優美，它定義了：

1）當 Xi 具有最大區域性密度時，δi 表示 S 中與 Xi 距離最大的資料點與 Xi 之間的距離；
2）否則，δi 表示在所有區域性密度大於 Xi 的資料點中（即其他cluster centers），與 Xi 距離最小的那個（或那些）資料點與 Xi 之間的距離。

0x3：聚類過程

至此，對於 S 中的每一個資料點 Xi，可以通過進行抽象表徵。考慮下圖的例子，其中包含28個二維資料點，將二元對在平面上畫出來。

我們看到，1號和10號資料點由於同時具有較大的區域性密度和類間距離，於是從資料集中“脫穎而出（pop up）”了，而這兩個資料點恰好是左圖中資料集的兩個聚類中心。

此外，26，27，28這三個資料點在原始資料集中是“離群點”，它們在右圖中也很有特點：其區域性密度很小，類間距離很大。

從直觀上來理解，上面右圖對確定聚類中心（cluster centers）有決定性作用，因此也將這種由對應的圖稱為決策圖（decision graph）。

聚類中心確定之後，剩餘點被分配給與其具有較高密度的最近鄰居相同的類簇。與其他迭代優化的聚類演算法不同，類簇分配在單個步驟中執行。

在聚類分析中, 通常需要確定每個點劃分給某個類簇的可靠性。

在該演算法中, 可以首先為每個類簇定義一個邊界區域（border region）， 亦即劃分給該類簇但是距離其他類簇的點的距離小於dc的點，這個區域中的點集可以認為是圈出了聚類中心的整體。然後為每個類簇找到其邊界區域的區域性密度最大的點，該類簇中所有區域性密度大於該點的區域性密度的點被認為是類簇核心的一部分（亦即將該點劃分給該類簇的可靠性很大），其餘的點被認為是該類簇的光暈， 亦即可以認為是噪音（outlier）。

圖A表示點分佈，其中包含非球形點集和雙峰點集。B和C分別表示4000和1000個點按照A中模式的分佈，其中點根據其被分配的不同類簇著色，黑色的點屬於類簇光暈。D和E是對應的決策圖，而F表示的是不同點量下不正確聚類點的比率，誤差線代表平均值的標準差。

下圖是分別利用點集和Olivetti臉部圖片集的聚類結果

0x4：演算法形式化描述

設待聚類資料集，其包含個cluster

值得注意的是，該聚類演算法得到的聚類中心可以作為其他聚類演算法（例如k-means）的初始聚類中心。

Relevant Link:

http://science.sciencemag.org/content/344/6191/1492
https://segmentfault.com/a/1190000011337432
https://blog.csdn.net/itplus/article/details/38926837

 

6. SOM（Self-organizing Maps） - 基於模型的聚類（model-based methods）

基於模型的方法給每個聚類假定一個模型（預先設定），然後尋找能夠很好地滿足這個模型的資料集。這樣一個模型可能是資料點在空間中的密度分佈函式或者其他。它的一個潛在的假定就是：

目標資料集是由一系列的概率分佈所決定的

通常有兩種嘗試方向：統計方案；和神經網路方案

關於神經網路方案方面的討論可以參閱我之前的一篇blog

Relevant Link:

http://www.cnblogs.com/LittleHann/p/7101992.html

Copyright (c) 2018 LittleHann All rights reserved

相關文章