1. 概率思想與歸納思想
0x1：歸納推理思想
所謂歸納推理思想，即是由某類事物的部分物件具有某些特徵，推出該類事物的全部物件都具有這些特徵的推理。抽象地來說，由個別事實概括出一般結論的推理稱為歸納推理（簡稱歸納），它是推理的一種
1. 歸納推理的分類
傳統上，根據前提所考察物件範圍的不同，把歸納推理分為
1. 完全歸納推理：考察某類事物的全部物件 2. 不完全歸納推理：僅考慮某類事物的部分物件，並進一步根據：所依據的前提是否揭示物件與其屬性間的因果聯絡，把不完全歸納推理分為 1）簡單列舉歸納推理：在經驗觀察基礎上所做出的概括 2）科學歸納推理：在科學實驗基礎上所做出的概括
這裡的所謂的“物件與其屬性間的因果聯絡”即歸納推理強度，歸納推理的強度彼此間差異很大，根據歸納強度可分為
1. 演繹推理：必然性推理 2. 歸納推理：或然性推理
而現代歸納推理的主要形式有
1. 列舉論證 2. 類別 3. 比喻論證 4. 統計論證 5. 因果論證
2. 歸納推理的必要條件
歸納推理的前提是其結論的必要條件，但是歸納推理的前提必須是真實的，否則歸納就失去了意義
3. 歸納推理的結論 - 即樣本
歸納推理裡的結論指的是觀測到了已經發生的事物結果，具體到機器學習領域就是我們常說的樣本。需要特別注意的是，前提是真不能保證結論也一定是真，有時候歸納推理的結論可能是假的，或者不完全是真的。如根據某天有一隻兔子撞到樹上死了，推出每天都會有兔子撞到樹上死掉，這一結論很可能為假，除非一些很特殊的情況發生
0x2：列舉推理 - 不完全推理的一種
在日常思維中，人們常根據對一類事物的部分物件具有某種屬性的考慮，推出這一類事物的全部物件或部分物件也具有該屬性的結論，這種推理就是列舉推理，即從特殊到一般的推理過程
例如：數目有年輪，從它的年輪知道樹木生長的年數；動物也有年輪，從烏龜甲上的環數可以知道它的年齡，牛馬的年輪在牙齒上，人的年輪在腦中。從這些事物推理出所有生物都有記錄自己壽命長短的年輪。
我們稱被考察的那部分物件為樣本（S），樣本中某一個物件為樣本個體（s），稱這一類事物的全部物件為總體（A），樣本屬性（P），總體所具有的屬性稱為描述屬性
列舉推理是從所考察的樣本屬性概括出總體屬性的推理，其推理形式如下：
A 的 S 都具有 P 屬性 => 所有 A 都具有 P 屬性
列舉推理是典型的歸納推理，因為它體現了歸納概括這個概念的實質。從哲學的認識論意義上說，演繹體現了由一般到個別的認識過程，歸納體現了由個別到一般的認識過程，二者是互相聯絡、互相補充的
如果一個總體中的所有個體在某一方面都具有相同的屬性，那麼任意一個個體在這方面的屬性都是總體的屬性（普遍寓於特殊中）
例如醫生為病人驗血只需抽取病人血液的一小部分。母親給嬰兒餵奶只要嘗一小口就能知道奶的溫度，不同的個體在某方面所具有的無差別的屬性稱為同質性，有差別的屬性稱為異質性。比較而言，在科學歸納中，樣本屬性與描述屬性具有同質性的概率較高，而在簡單列舉法中，樣本屬性與描述屬性具有同質性的概率較低
1. 全稱列舉推理的批判性準則
1. 沒有發現與觀測結論相關的反例：只要有與結論相關的反例，無論有多少正面支援結論的例項，結論都是不真實的 2. 樣本容量越大，結論的可靠型就越大：基於過少的樣本所作出的概括是容易犯錯誤的，我們需要足夠大的樣本容量，也就是樣本內所含個體的數量，才能確立我們對所作出的概括的信心 3. 樣本的個體之間的差異越大，結論的可靠性就越大：樣本個體之間的差異通常能反映樣本個體在總體中的分佈情況，樣本個體之間的差異越大說明樣本個體在總體中的分佈越廣。這條準則涉及樣本的代表性問題 4. 樣本屬性與描述屬性有同質性的概率越大，結論的可靠性越大：從邏輯上說，樣本屬性與結論所概括概括的總體屬性應當具有同質性，否則就一定會有反例。對於機器學習來說，就是我們取的樣本一定要是最終實際線上模型的獲取方式、特徵抽取提取方式等方面一定要保持一致，這樣才能保證同質性
2. 特稱列舉與單稱列舉
在一類事物中，根據所觀察的樣本個體具有某種屬性的前提，得出總體中的其他一些個體也具有這種屬性的結論，這種推理就是特稱列舉推理，例如
1. 在亞洲觀察到的天鵝是白色的，在歐洲和非洲觀察到的天鵝也是白色的。所以美洲的天鵝也是白的：特稱列舉是從樣本到樣本的推理 2. 在亞洲觀察到的天鵝是白色的，在歐洲和非洲觀察到的天鵝也是白色的，所以隔壁小李叔叔救回來的那隻受傷的天鵝也會是白的：單稱推理是從已考察的樣本S到未知個體
需要注意的是，上面提到的4個全稱列舉的準則都同樣應用於特徵列舉與單稱列舉，但是存在幾個問題
1. 由於單稱列舉和特稱列舉的結論是對未知個體做出的斷定，結論超出了前提的斷定範圍，其結論面臨著更大的反例的可能性，例如小李叔叔救回來的天鵝不是白色的，或者根本就不是天鵝 2. 在日常思維實際中，單稱列舉和特稱列舉所推斷的情況往往在未來才會出現。因而也稱之為預測推理，其中單稱列舉推理是最常用的形式，例如：從過去太陽總是從東方升起，推斷出明天太陽也將從東方升起
0x3：完全歸納法 - 列舉推理的極限
如果前提所包含的樣本個體窮盡了總體中的所有個體 ，則其結論具有必然的性質。完全歸納法的特點是前提所考察的一類物件的全部，結論斷定的範圍沒有超出前提的斷定範圍，本質上屬於演繹推理
0x4：概率思想和歸納思想的聯絡
概率思想與歸納思想之間存在密切聯絡。歸納法中的概率歸納推理是從歸納法向概率法發展的標誌。概率歸納推理是根據一類事件出現的概率，推出該類所有事件出現的概率的不完全歸納推理，是由部分到全體的推理，其特點是對可能性的大小作數量方面的估計，它的結論超出了前提所斷定的範圍，因而是或然的。
從某種程度上來說，歸納是一種特殊的概率，概率方法是歸納方法的自然推廣，概率是歸納法發展到一定程度的必然產物
1. 概率法 1） 概率法本身是對大量隨機事件和隨機現象所進行的一種歸納，是對隨機事件發生的結果的歸納，它並不關心事件發生的具體過程 2）而概率方法則主要適用於多變數因果關係的複雜事件所決定的問題 2. 歸納法 1）歸納法不僅關注事件發生的結果，它還關注事件發生的具體過程，它承認事件發生過程中的規律性，並以此為基礎來研究事件發生過程中的規律性 2）歸納法主要適用於少變數因果關係的簡單事件所決定的問題
0x5：統計思想（數理統計）與特殊化思想的聯絡
特殊化思想是將研究物件或問題從一般狀態轉化為特殊狀態進行考察和研究的一種思想方法。特殊化思想方法的哲學基礎是矛盾的普遍性寓於特殊性之中。
而數理統計思想方法是通過對樣本的研究來把握總體內在規律的一種研究方法，換句話說，統計是通過對特殊事物的認識來把握一般規律，因此它也是一種特殊思想方法
特殊化方法主要處理確定性問題，更側重過程和對具體方法的把握；而統計法則主要研究隨機物件，它更強調對結果和整體的把握。
數量統計思想並不侷限在具體的方法層次，它主要是從思想層面來把握問題，是一種真正意義上的特殊化方法
Relevant Link:
http://www.doc88.com/p-2985317492201.html https://max.book118.com/html/2014/0104/5473598.shtm http://www.docin.com/p-355028594.html https://baike.baidu.com/item/歸納推理思想/8335575?fr=aladdin http://www.360doc.com/content/12/0312/15/7266134_193751535.shtml
2. 概率論和統計學的關係
來自於微博的一張圖：
1. 概率論是統計推斷的基礎，在給定資料生成過程下觀測、研究資料生成的性質； 2. 而統計推斷則根據觀測的資料，反向思考其資料生成過程。預測、分類、聚類、估計等，都是統計推斷的特殊形式，強調對於資料生成過程的研究。
例如：在醫院會對過去有糖尿病的所有病人進行歸納總結（建立模型，即統計歸納）；當有一個新的病人入院時，就可以用之前的歸納總結來判斷該病人是否患糖尿病，然後就可以對症下藥了。統計裡常說的“分類”就是這個過程（即根據已知條件進行預測未來）。
統計＝樣本(回顧過去的資料)歸納出總體(總結)
概率率＝總體(給定條件)對樣本進行預測
統計和概率是方法論上的區別，概率是演繹（分析），統計是歸納（總結）
1. 概率論研究的是一個白箱子，你知道這個箱子的構造（裡面有幾個紅球、幾個白球，也就是所謂的聯合概率分佈函式），然後計算下一個摸出來的球是紅球的概率（求具體條件概率） 2. 而統計學面對的是一個黑箱子，你只看得到每次摸出來的是紅球還是白球，然後需要猜測這個黑箱子的內部結構，例如紅球和白球的比例是多少？（引數估計）能不能認為紅球40%，白球60%？（假設檢驗）
0x1：統計歸納合理性的理論基石 - 概率正態分佈定理和概率期望定理
1. 小數定理
如果統計資料不夠大，就什麼也說明不了
小數定律裡的“跟它的期望值一點關係都沒有”，這裡的期望值就是接下來要討論的“大數定律”。2. 大數定理 - 隨機變數的平均結果問題
大數定律是我們從統計數字中推測（歸納）真相的理論基礎。
大數定律說如果統計資料足夠大，那麼事物出現的頻率（統計）就能無限接近他的期望值（概率）
所謂期望，在我們的生活中，期望是你希望一件事情預期達到什麼樣的效果。例如，你去面試，期望的薪水是1萬5。
在統計概率裡，期望也是一樣的含義，表示的也是事件未來的預期值，只不過是用更科學的方式來計算出這個數值。某個事件的期望值，也就是收益，實際上是所有不同結果的和，其中每個結果都是由各自的概率和收益相乘而來。
1/6*1元+1/6*2元+1/6*3美元）+1/6*4元+1/6*5元+1/6*6元 =3.5元
這個期望3.5元代表什麼意思呢？
可能你某一次拋篩子贏了1元，某一次拋篩子贏了6元，但是長期來看（假設玩了無數盤），你平均下來每次的收益會是3.5元。
1. 我們發現當拋篩子次數少數，期望波動很大。這就是小數定律，如果統計資料很少，那麼事件就表現為各種極端情況，而這些情況都是偶然事件，跟它的期望值一點關係都沒有。 2. 但是當你拋篩子次數大於60次後，就會越來越接近它的期望值3.5。
3. 概率中的收斂定理 - 隨機變數的概率分佈問題
按分佈收斂 - 中心極限定理
在一定條件下，大量獨立隨機變數的平均數是以正態分佈為極限的。根據中心極限定理，我們通過大量獨立隨機變數的統計歸納，可以得到概率分佈密度函式的近似值
列維-林德伯格定理
棣莫弗—拉普拉斯定理
證明的是二項分佈的極限分佈是正態分佈，也告訴了我們實際問題時可以用大樣本近似處理。0x2：為什麼在大量實驗中隨機變數的統計結果可以歸納推理出概率密度函式？
0x3：機器學習場景中大多數是統計歸納問題，目的是近似得到概率
統計是由樣本資訊反推概率分佈，如概率分佈引數的點估計、區間估計，以及線性迴歸、貝葉斯估計等Relevant Link:
https://www.zhihu.com/question/19911209 https://baike.baidu.com/item/大數定律/410082?fr=aladdin https://www.zhihu.com/question/20269390 https://www.zhihu.com/question/20269390 http://blog.csdn.net/linear_luo/article/details/52760309 https://betterexplained.com/articles/a-brief-introduction-to-probability-statistics/
3. 似然函式
前面兩個章節討論了統計歸納可以推匯出概率密度，以及背後的數學理論支撐基礎。所以接下來的問題就是另一個問題了，how？我們如何根據一個實驗結果進行統計歸納計算，得到一個概率密度的估計？根據實驗結果歸納統計得到的這個計算得到的是一個唯一確定值嗎？
0x1：似然與概率密度在概念上不等但是在數值上相等 - 因果論的一種典型場景
首先給出一個等式：
等式左邊表示給定聯合樣本值
條件下關於未知引數
的函式；等式右邊的
是一個密度函式，它表示給定引數下關於聯合樣本值的聯合密度函式
從數學定義上，似然函式和密度函式是完全不同的兩個數學物件：
是關於的函式，是關於的函式，但是神奇地地方就在於它們的函式值形式相等，實際上也可以理解為有因就有果，有果就有因
這個等式表示的是對於事件發生的兩種角度的看法，本質上等式兩邊都是表示的這個事件發生的概率或者說可能性
1. 似然函式 L(θ|x)：再給定一個樣本x後，我們去想這個樣本出現的可能性到底是多大。統計學的觀點始終是認為樣本的出現是基於一個分佈的。那麼我們去假設這個分佈為 f，裡面有引數theta。對於不同的theta，樣本的分佈不一樣，所有的theta對應的樣本分佈就組成了似然函式 2. 概率密度函式 f(x|θ)：表示的就是在給定引數theta的情況下，x出現的可能性多大。
所以其實這個等式要表示的核心意思都是在給一個theta和一個樣本x的時候，整個事件發生的可能性多大。
0x2：概率密度函式和似然函式數值相等的一個例子
以伯努利分佈（Bernoulli distribution，又叫做兩點分佈或0-1分佈）為例：
也可以寫成以下形式：
，
表示觀測結果的不確定性1. 從概率密度函式角度看
是關於引數 p 的函式，即 f 依賴於 p 的值。
對於任意的引數 pp 我們都可以畫出伯努利分佈的概率圖，當 p = 0.5 時：f(x) = 0.5。這表明引數 p = 0.5時，觀測結果的不確定性是對半開的
我們可以得到下面的概率密度圖：
可以看到，引數 p 的取值越偏離0.5，則意味著觀測結果的不確定性越低
2. 從似然函式角度看
從似然的角度出發，假設我們觀測到的結果是 x = 0.5（即某一面朝上的概率是50%，這個結果可能是通過幾千次幾萬次的試驗得到的），可以得到以下的似然函式：
注意：這裡的 π 描述的是伯努利實驗的效能而非事件發生的概率（例如 π = 0.5 描述的一枚兩面均勻的硬幣）
對應的似然函式圖是這樣的：
我們很容易看出似然函式的極值（也是最大值）在 p = 0.5 處得到，通常不需要做圖來觀察極值，令似然函式的偏導數為零即可求得極值條件。偏導數求極值是最最大似然函式的常用方法
0x3：似然函式的極大值
似然函式的最大值意味著什麼？讓我們回到概率和似然的定義，概率描述的是在一定條件下某個事件發生的可能性，概率越大說明這件事情越可能會發生；而似然描述的是結果已知的情況下，該事件在不同條件下發生的可能性，似然函式的值越大說明該事件在對應的條件下發生的可能性越大。
現在再來看看之前提到的拋硬幣的例子：
上面的 π （硬幣的性質）就是我們說的事件發生的條件，
描述的是性質不同的硬幣，任意一面向上概率為50% 的可能性有多大，
在很多實際問題中，比如機器學習領域，我們更關注的是似然函式的最大值，我們需要根據已知事件來找出產生這種結果最有可能的條件，目的當然是根據這個最有可能的條件去推測未知事件的概率。在這個拋硬幣的事件中，π 可以取 [0, 1] 內的所有值，這是由硬幣的性質所決定的，顯而易見的是 π = 0.5 這種硬幣最有可能產生我們觀測到的結果。
0x4：對數化的似然函式
對數似然函式並不是一個新的概念，它只是一個具體實現上的優化做法，因為實際問題往往要比拋一次硬幣複雜得多，會涉及到多個獨立事件，在似然函式的表示式中通常都會出現連乘：
對多項乘積的求導往往非常複雜，但是對於多項求和的求導卻要簡單的多，對數函式不改變原函式的單調性和極值位置，而且根據對數函式的性質可以將乘積轉換為加減式，這可以大大簡化求導的過程：
在機器學習的公式推導中，經常能看到類似的轉化。
0x5：概率密度函式和似然函式數值相等的另一個例子 - 擲硬幣問題
考慮投擲一枚硬幣的實驗。通常來說，已知投出的硬幣正面朝上和反面朝上的概率各自是
，便可以知道投擲若干次後出現各種結果的可能性
比如說，投兩次都是正面朝上的概率是0.25。用條件概率表示，就是：
，其中H表示正面朝上。
在統計學中的大多數場景中，我們關心的是在已知一系列投擲的結果時，關於硬幣投擲時正面朝上的可能性的資訊。我們可以建立一個統計模型：假設硬幣投出時會有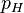
的概率正面朝上，而有
的概率反面朝上。
這時，條件概率可以改寫成似然函式：
也就是說，對於取定的似然函式，在觀測到兩次投擲都是正面朝上時， 的似然性是0.25（這並不表示當觀測到兩次正面朝上時 的概率是0.25）。
如果考慮
，那麼似然函式的值也會改變。
這說明，如果引數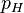 的取值變成0.6的話，結果觀測到連續兩次正面朝上的概率要比假設 時更大。也就是說，引數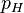 取成0.6 要比取成0.5 更有說服力，更為“合理”
仔細思考，我們就會發現，L 是關於 PH的單調遞增函式，如下圖：
怎麼理解這張圖？即在實驗結果已知的 HH 情況下，最大似然估計認為最有可能的情況是PH的概率為1，即這個硬幣100%都是正面（雖然我們知道這不合理，但是反映了實驗樣本對似然估計合理性的影響）
總之，似然函式的重要性不是它的具體取值，而是當引數變化時函式到底變小還是變大。對同一個似然函式，如果存在一個引數值，使得它的函式值達到最大的話，那麼這個值就是最為“合理”的引數值。Relevant Link:
https://en.wikipedia.org/wiki/Maximum_likelihood_estimation https://www.zhihu.com/question/54082000 http://fangs.in/post/thinkstats/likelihood/ https://zhuanlan.zhihu.com/p/22092462 http://blog.csdn.net/sunlylorn/article/details/19610589 https://www.cnblogs.com/zhsuiy/p/4822020.html https://zhuanlan.zhihu.com/p/26614750 https://www.zhihu.com/question/48230067 https://zhuanlan.zhihu.com/p/22092462 http://fangs.in/post/thinkstats/likelihood/
4. 極大似然估計
極大似然估計是一種估計資料引數的常見統計方法，它遵循的準則是極大似然準則。極大似然準則和經驗風險最小化準則一樣，都是一種計算模型概率分佈引數的準則，我們後面會討論它們的區別。
0x1：從模型引數估計的角度談極大似然估計
筆者觀點：最大似然估計是利用已知的樣本的結果，在使用某個模型的基礎上，反推最有可能導致這樣結果的模型引數值。
1. 伯努利分佈下的極大似然引數估計
假設一個袋子裝有白球與紅球，比例未知，現在抽取10次（每次抽完都放回，保證事件獨立性）。
假設抽到了7次白球和3次紅球，在此資料樣本條件下，可以採用最大似然估計法求解袋子中白球的比例（最大似然估計是一種“模型已定，引數未知”的方法）。
我們知道，一些複雜的問題，是很難通過直觀的方式獲得答案的，這時候理論分析就尤為重要了，我們可以找到一個"逼近模型"來無限地逼近我們要處理的問題的本質
我們可以定義2次實驗中從袋子中抽取白球和紅球的概率如下
x1為第一次取樣，x2為第二次取樣，f為模型, theta為模型引數，X1，X2是獨立同分布的
其中theta是未知的，因此，我們定義似然L為：
L為似然的符號
因為目標是求最大似然函式，因此我們可以兩邊取ln，取ln是為了將右邊的乘號變為加號，方便求導(不影響極大值的推導)
兩邊取ln的結果，左邊的通常稱之為對數似然
最大似然估計的過程，就是找一個合適的theta，使得平均對數似然的值為最大。因此，可以得到以下公式：
最大似然估計的公式
我們寫出擴充到n次取樣的情況
最大似然估計的公式（n次取樣）
我們定義M為模型（也就是之前公式中的f），表示抽到白球的概率為theta，而抽到紅球的概率為(1-theta)，因此10次抽取抽到白球7次的概率可以表示為：
10次抽取抽到白球7次的概率
將其描述為平均似然可得：
那麼最大似然就是找到一個合適的theta，獲得最大的平均似然(求最大極值問題)。因此我們可以對平均似然的公式對theta求導，並另導數為0
求導過程
由此可得，當抽取白球的概率為0.7時，最可能產生10次抽取抽到白球7次的事件。
筆者思考：
如果我們的實驗結果是：前10次抽到的球都是白球，則對對數似然函式進行求導，並另導數為0，得出theta為1，即當取白球的概率是100%時，最有可能10次都抽到白球。 顯然，這種"推測結果"很容易"偏離真實情況"，因為很可能是因為10次都抽到白球這種小概率事件導致我們基於觀測值的最大似然推測失真，即產生了過擬合，但是造成這種現象的本質是因為"我們的訓練樣本未能真實地反映待推測問題的本質"，在一個不好的樣本集下，要做出正確的預測也就變得十分困難。
2. 正態分佈下的極大似然引數估計
我們前面說了，事物的本來規律是很複雜的，我們很難用一個百分百準確的模型去描述事物的本質，但是我們可以用一些類似的通用模型去"儘可能逼近"事物的本質。
高斯分佈(正態分佈)一種非常合理的描述隨機事件的概率模型。
假如有一組取樣值（x1,...,xn），我們知道其服從正態分佈，且標準差已知。當這個正態分佈的期望和方差為多少時，產生這個取樣資料的概率為最大？
繼續上個小節的例子：
基於n次實驗觀測值對引數theta預測的的似然函式
正態分佈的公式，當第一引數（期望）為0，第二引數（方差）為1時，分佈為標準正態分佈
把高斯分佈函式帶入n次獨立實驗的似然函式中
對上式求導可得，在高斯分佈下，引數theta的似然函式的值取決於實驗觀測結果，這和我們上例中抽球實驗是一致的
筆者思考：根據概率原理我們知道，如果我們的實驗次數不斷增加，甚至接近無限次，則實驗的觀測結果會無限逼近於真實的概率分佈情況，這個時候最大似然函式的估計就會逐漸接近真實的概率分佈，也可以這麼理解，樣本觀測量的增加，會降低似然函式過擬合帶來的誤差。
0x2：極大似然估計和經驗風險最小化準則的關係
極大似然估計準則和經驗風險最小化準則（ERM），是具有一定的相似性的。
在經驗風險最小化原則中，有一個假設集
，利用訓練集進行學習，選取假設
，實現使得經驗風險最小化。實際上，極大似然估計是對於特定的損失函式的經驗風險最小化，也就說，極大似然估計是一種特殊形式的經驗風險最小化。
對於給定的引數
和觀測樣本 x，定義損失函式為：
也就是說，假設觀測樣本 X 服從分佈
，損失函式
與 x 的對數似然函式相差一個負號。該損失函式通常被稱為對數損失。
在基礎上，可以驗證，極大似然準則等價於上式定義的對數損失函式的經驗風險最小化（僅限於對數損失函式）
這裡我們可以這麼理解：經驗風險最小化是一種泛化的模型求參法則，它的核心是求極值。而極大似然是一種特殊的形態，即使用對數這種形式來進行極值求導。
資料服從的潛在分佈為 P（不必滿足引數化形式），引數的真實風險為：
其中，
稱為相對熵，H 稱為熵函式。
相對熵是描述兩個概率分佈的差異的一種度量。對於離散分佈，相對熵總是非負的，並且等於 0 當且僅當兩個分佈是相同的。
由此可見，當
時，真實風險達到極小值。
同時，上式還刻畫了生成式的假設對於密度估計的影響，即使是在無窮多樣本的極限情況下，該影響依然存在。如果潛在分佈具有引數化的形式，那麼可以通過選擇合適的引數，使風險降為潛在分佈的熵。
然而，如果潛在分佈不滿足假設的引數化形式，那麼即使由最優引數所確定的模型也可能是較差的，模型的優劣是用熵刻畫的。
上面的討論總結一下本質就是估計風險和逼近風險的概念：
1. 估計風險：我們的生成式假設是否足夠逼近真實的潛在分佈？ 2. 逼近風險：我們的訓練樣本能否支援模型得到合適的模型引數？
0x3：最大似然估計和最小二乘法的聯絡
線性迴歸中的最小二乘（OLSE）的策略思想是使擬合出的目標函式和所有已知樣本點儘量靠近，本質上我們可以將擬合線（linear function）看成是一種對樣本概率密度分佈的表示，這樣有利於我們去思考最大似然和最小二乘法在本質上的聯絡。
1. 最大似然估計:
現在已經拿到了很多個樣本（資料集中包含所有因變數），這些樣本值已經實現，最大似然估計就是去找到那個（組）引數估計值，使得前面已經實現的樣本值發生概率最大。
因為你手頭上的樣本已經實現了，其發生概率最大才符合邏輯。這時是求樣本所有觀測的聯合概率最大化，是個連乘積，只要取對數，就變成了線性加總。
此時通過對引數求導數，並令一階導數為零，就可以通過解方程（組），得到最大似然估計值。
2. 最小二乘:
找到一個（組）估計值，使得實際值與估計值的距離最小。
這裡評估實際值和估計值之間距離的函式就叫“損失函式”，一個常用的損失函式是平方和損失，找一個（組）估計值，使得實際值與估計值之差的平方加總之後的值最小，稱為最小二乘。
這時，將這個差的平方的和式對引數求導數，並取一階導數為零，就是OLSE。
論及本質，其實兩者只是用不同的度量空間來進行的投影：
最小二乘（OLS）的度量是L2 norm distance；
而極大似然的度量是Kullback-Leibler divergence（KL散度）；
1. 一個例子說明最大似然和最小二乘區別
設想一個例子，教育程度和工資之間的關係。我們可以觀察到的資料是：教育程度對應著一個工資的樣本資料
1）OLS的做法
我們的目標是找到兩者之間的規律，如果樣本集中只有2個點，則計算是非常簡單的，既不需要OLS也不需要最大似然估計，直接兩點連成一條線即可。但是我們知道OLS和最大似然都是一種數學工具，它要解決的情況就是大量樣本集時的數學計算問題。
如果我們的學歷-工資樣本集大數量到達3個點，且這3個點不共線，那顯然我們就無法通過肉眼和直覺判斷直接得到linear regression function了。如下圖：
如果這三個點不在一條線上，我們就需要作出取捨了，如果我們取任意兩個點，那麼就沒有好好的利用第三個點帶來的新資訊，並且因為這三個點在資料中的地位相同，我們如何來斷定應該選用哪兩個點來作為我們的基準呢？這就都是問題了。
這個時候我們最直觀的想法就是『折衷』一下，在這三個資料，三條線中間取得某種平衡作為我們的最終結果，類似於上圖中的紅線這樣。
那接下來的問題就是，怎麼取這個平衡了？
我們需要引入一個數學量化的值：誤差，也就是我們要承認觀測到的資料中有一些因素是不可知的，不能完全的被學歷所解釋。而這個不能解釋的程度自然就是每個點到紅線在Y軸的距離。
有了誤差這個度量的手段，即我們承認了有不能解釋的因素，但是我們依然想盡可能的讓這種『不被解釋』的程度最小，於是我們就想最小化這種不被解釋的程度。因為點可能線上的上面或者下面，故而距離有正有負，取絕對值又太麻煩，於是我們就直接把每個距離都取一個平方變成正的，然後試圖找出一個距離所有點的距離的平方最小的這條線，這就是最小二乘法了。
2）極大似然的做法
極大似然的估計則更加抽象一些，我們觀察到了這3個點，說明這3個點是其背後“真實規律模型對應的資料集”中選出的最優代表性的3個，所以我們希望找到一個特定的底薪和教育增量薪水的組合，讓我們觀察到這三個點的概率最大，這個找的過程就是極大似然估計。
極大似然估計是尋找一個概率函式分佈，使之最符合現有觀測到的樣本資料。
筆者思考：在神經元感知機演算法中，求損失函式最小值（經驗風險最小）尋找分介面的本質和極大似然求解是一樣的，都是在尋找一個有最大概率產生當前觀察樣本的模型。
Relevant Link:
https://zhuanlan.zhihu.com/p/24602462 https://www.zhihu.com/question/26201440 https://en.wikipedia.org/wiki/Kullback%E2%80%93Leibler_divergence https://www.zhihu.com/question/20447622 http://blog.csdn.net/feilong_csdn/article/details/61633180 https://www.cnblogs.com/ChengQH/p/e5dd604ee211533e50187c6fd37787bd.html
5. 貝葉斯估計 - 包含先驗假設（正則化）的極大似然估計
0x1：貝葉斯估計是對極大似然估計的一種改進
最大似然估計存在一定的缺陷
1. 最大似然估計屬於點估計，只能得到待估計引數的一個值。但是在有的時候我們不僅僅希望知道，我們還希望知道取其它值得概率，即我們希望知道整個在獲得觀察資料後的分佈情況 2. 最大似然估計僅僅根據(有限的)觀察資料對總體分佈進行估計，在資料量不大的情況下，可能不準確。
例如我們要估計人的平均體重，但是抽樣的人都是小孩，這樣我們得到的平均體重就不能反映總體的分佈，而我們應該把“小孩之佔總人口20%”的先驗考慮進去。這時我們可以用貝葉斯方法。
貝葉斯估計和最大似然估計最大的區別我認為在於：
貝葉斯估計對假設空間的概率分佈有一個預先的假設（先驗），而不是完全無腦地信任觀測樣本資料，它相當於先建立一個初始基線值，然後根據觀測樣本值去不斷修正它，這樣修正後的結果具有很好的穩定性，不會隨著觀測樣本的波動而波動。
0x2：貝葉斯法則
貝葉斯法則又被稱為貝葉斯定理、貝葉斯規則，是指概率統計中的應用所觀察到的現象對有關概率分佈的主觀判斷（即先驗概率）進行修正(訓練過程中不斷修正)的標準方法。當分析樣本大到接近總體數時，樣本中事件發生的概率將接近於總體中事件發生的概率。
貝葉斯統計中的兩個基本概念是先驗分佈和後驗分佈：
1. 先驗分佈:
總體分佈引數θ的一個概率分佈。貝葉斯學派的根本觀點，是認為在關於總體分佈引數θ的任何統計推斷問題中，除了使用樣本所提供的資訊外，還必須規定一個先驗分佈，它是在進行統計推斷時不可缺少的一個要素。
他們認為先驗分佈不必有客觀的依據，可以部分地或完全地基於主觀信念。
2. 後驗分佈:
根據樣本分佈和未知引數的先驗分佈，用概率論中求條件概率分佈的方法，求出的在樣本已知下，未知引數的條件分佈。因為這個分佈是在抽樣以後才得到的，故稱為後驗分佈。
0x3：貝葉斯估計公式
貝葉斯估計，是在給定訓練資料D時，確定假設空間 H 中的最佳假設，一般定義為：
在給定資料 D 以及假設空間 H 中，不同的先驗概率下，最可能存在的後驗假設分佈。
貝葉斯估計的公式如下：
p(h|D) = P(D|H) * P(H) / P(D)
先驗概率用 P(h) 表示，它表示了在沒有訓練資料前假設 h 擁有的初始概率(訓練前的一個初始的先驗假設)。先驗概率反映了我們關於 h 分佈的主觀認知，如果我們沒有這一先驗知識，可以簡單地將每一候選假設賦予相同的先驗概率（平均概率也是一種合理的先驗假設）；
P(D)表示訓練資料D的先驗概率；
P( D | H )表示假設h成立時D的概率；
機器學習中，我們關心的是P( H | D )，即給定D時 H 的成立的概率，稱為 H 的後驗概率。
貝葉斯公式提供了從先驗概率P(h)、P(D)和P( D | H)計算後驗概率P(H|D)的方法，即提供了一種從現象回溯規律本質的方法。
對貝葉斯估計的公式，可以這麼來理解：
我們的目標P(H|D)，隨著P(h)和P(D|H)的增長而增長，隨著P(D)的增長而減少。
即如果D獨立於H時被觀察到的可能性越大，那麼D對h的支援度越小，或者說D中包含的對推測出h的有效資訊熵越小，即這是一份對我們的推測基本沒有幫助的資料。
Relevant Link：
http://www.cnblogs.com/jiangxinyang/p/9378535.html
6. 最大後驗估計 MAP - 包含先驗假設（正則化）的極大似然估計
0x1：MAP和貝葉斯估計的區別
對於最大後驗估計MAP，首先要說明的一點的是，最大後驗估計和我們上一章節討論的貝葉斯估計在數學公式上非常類似，在統計思想上也很類似，都是以最大化後驗概率為目的。區別在於：
1. 極大似然估計和極大後驗估計MAP只需要返回預估值，貝葉斯估計要計算整個後驗概率的概率分佈； 2. 極大後驗估計在計算後驗概率的時候，把分母p(D)給忽略了，在進行貝葉斯估計的時候則不能忽略；
0x2：MAP估計的數學公式
假設 x 為獨立同分布的取樣，θ為模型引數，f 為我們所使用的模型。那麼最大似然估計可以表示為：
現在，假設θ的先驗分佈為g。通過貝葉斯理論，對於θ的後驗分佈如下式所示：
後驗分佈的目標為：
，分母並不影響極大值的求導，因此可以忽略。
最大後驗估計可以看做貝葉斯估計的一種特定形式。
0x3：MAP估計舉例
假設有五個袋子，各袋中都有無限量的餅乾(櫻桃口味或檸檬口味)，已知五個袋子中兩種口味的比例分別是
櫻桃 100%
櫻桃 75% + 檸檬 25%
櫻桃 50% + 檸檬 50%
櫻桃 25% + 檸檬 75%
檸檬 100%
如果只有如上所述條件，那問從同一個袋子中連續拿到2個檸檬餅乾，那麼這個袋子最有可能是上述五個的哪一個？
我們知道，最大後驗概率MAP是正則化的最大似然概率，我們首先採用最大似然估計來解這個問題，寫出似然函式。
假設從袋子中能拿出檸檬餅乾的概率為p，則似然函式可以寫作：
由於p的取值是一個離散值，即上面描述中的0,25%，50%，75%，1。我們只需要評估一下這五個值哪個值使得似然函式最大即可，根據最大似然的計算，肯定得到為袋子5。
上述最大似然估計有一個問題，就是沒有考慮到模型本身的概率分佈(即沒有考慮模型本身的複雜度)(結構化風險)，下面我們擴充套件這個餅乾的問題。對模型自身的複雜度進行先驗估計
拿到袋子1的概率是0.1
拿到袋子2的概率是0.2
拿到袋子3的機率是0.4
拿到袋子4的機率是0.2
拿到袋子5的機率是0.1
# 類高斯分佈
那同樣上述問題的答案呢？這個時候就變MAP了。我們根據公式
寫出我們的MAP函式
根據題意的描述可知，p的取值分別為0，25%，50%，75%，1，g的取值分別為0.1，0.2，0.4，0.2，0.1。分別計算出MAP函式的結果為：
0 * 0 * 0.1 = 0
0.25 * 0.25 * 0.2 = 0.0125
0.5 * 0.5 * 0.4 = 0.1
0.75 * 0.75 * 0.2 = 0.1125
1 * 1 * 0.1 = 0.1
由上可知，通過MAP估計可得結果是從第四個袋子中取得的最高。
可以看到，雖然觀測結果表明最大似然應該是第5個袋子，但是在加入正則化(模型複雜度)先驗後，得到的結果被修正了。
Relevant Link：
https://lagunita.stanford.edu/c4x/Engineering/CS-224N/asset/slp4.pdf https://guangchun.wordpress.com/2011/10/13/ml-bayes-map/ https://en.wikipedia.org/wiki/N-gram http://www.jianshu.com/p/f1d3906e4a3e http://www.cnblogs.com/liliu/archive/2010/11/22/1883702.html http://www.cnblogs.com/xueliangliu/archive/2012/08/02/2962161.html http://www.cnblogs.com/stevenbush/articles/3357803.html http://blog.csdn.net/guohecang/article/details/52313046 http://www.cnblogs.com/burellow/archive/2013/03/19/2969538.html
Copyright (c) 2018 LittleHann All rights reserved