0. 從貝葉斯最優分類器說起
討論樸素貝葉斯之前，我們先來討論一下貝葉斯最優分類器，它和樸素貝葉斯一樣，都是一種生成式模型。
對於給定的特徵向量
，我們的目的是預測樣本的標籤
。假定每個
都屬於{0，1}，，貝葉斯最優分類器的函式形式是：
為了描述概率函式
，我們需要
個引數，每個對應於給定一個
時概率函式
的值，這意味著，我們所需的樣本數量隨特徵個數呈現指數型增長。
這對樣本的數量往往會有很大的要求，在實際的工程中很多時候是不可實現的。
0x1：如何對貝葉斯最優分類器的假設類進行限制？
我們知道，在PAC可學習理論中，通過限制假設類可以緩解欠擬合問題，同時減小逼近誤差，雖然可能會引入估計誤差增大的問題。
在樸素貝葉斯方法中，我們給出的樸素的生成式假設是：對於給定的標籤，各特徵之間是彼此獨立的，即：
有了這種約束假設，並使用貝葉斯法則，貝葉斯最優分類器可簡化為：
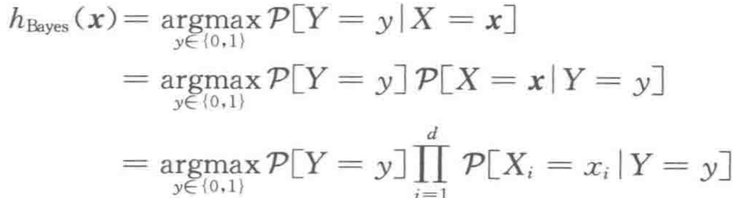
也就是說，對於樸素貝葉斯生成式推測來說，需要估計的引數個數只有 2d+1 個。這個獨立假設顯著減少了需要學習的引數數量。
因此，當我們使用最大似然原則進行引數估計時，得到的分類被稱為樸素貝葉斯分類器。
1. 樸素貝葉斯法的模型定義
樸素貝葉斯（naive Bayes）法是基於貝葉斯定理與特徵條件獨立假設的分類方法。對於給定的訓練資料集，首先基於特徵條件獨立假設學習輸入/輸出的聯合概率分佈；然後基於此模型，對給定的輸入x，利用貝葉斯定理求出後驗概率最大的輸出y
0x1：樸素貝葉斯模型是生成模型（generative model）
樸素貝葉斯法實際上學習到生成資料的機制，所以屬於生成模型
樸素貝葉斯法模型訓練的目標是學習到樣本中包含的輸入/輸出的聯合概率分佈，這就對訓練樣本的質量提出了要求，即要求樣本（提取的特徵）需要包含真實有效的概率分佈資訊
所有的機器學習演算法的前提都是概率同分佈，就是訓練樣本的分佈空間必須與實際問題的分佈空間相同
只有我們的訓練樣本中的的確確包含了代表問題本質的規律結構，演算法才有機會去學習到這種模式)
這樣訓練出來的模型泛化效能才會好，也就是模型預測未知資料的準確性好
我們在應用機器學習/深度學習來解決安全問題的時候，首先需要思考的問題是：我們的樣本資料是怎麼樣的？我們要用什麼方式去抽象我們的樣本資料？不同的抽象方式又代表了我們如何看待樣本的角度。如果我們取樣抽取的樣本特徵空間不足以真實地描述我們要預測的問題本質；或者是我們的樣本量不夠，在這種情況下，再好的演算法也無法獲得一個好的效果
0x2：樸素貝葉斯模型
1. 模型訓練 - 輸入X/輸出Y的聯合概率分佈
設輸入空間
為 n 維向量的集合，輸出空間為類標記集合 Y = ｛C1，C2，...，Ck｝，輸入為特徵向量
，輸出為類標記（class label）
。
是X和Y的聯合概率分佈，訓練資料集
由獨立同分布產生。
樸素貝葉斯法通過訓練資料集學習聯合概率分佈， 但聯合概率不能直接產生（事實上它是未知的），樸素貝葉斯通過以下先驗概率及條件概率分佈，並通過貝葉斯定理計算得到聯合概率
先驗概率分佈：
條件概率分佈：
先驗概率
和條件概率
相乘得到聯合概率
2. 模型預測 - 選擇後驗概率最大對應的類
樸素貝葉斯法分類時，對給定的輸入x，通過學習到的模型計算後驗概率分佈
，將後驗概率最大的類作為 x 的預測類輸出，後驗概率計算根據貝葉斯定理進行：
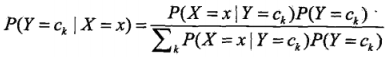，將條件獨立假設帶入公式得：
這是樸素貝葉斯法分類預測的基本公式，得到當時輸入對應的每個類別的後驗概率後，樸素貝葉斯從中選出後驗概率最大的那一個類作為預測結果，即：
同時，注意到上式中分母對所有Ck都是相同的，因此分母可約掉，得：
0x3：樸素貝葉斯的條件獨立性假設
條件概率有指數級數量的引數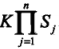
（所有引數的排列組合），直接估計實際上是不可行的。為了解決這個問題，樸素貝葉斯非對條件概率分佈加了一個條件獨立性假設，由於這是一個較強的假設，樸素貝葉斯法也因此得名
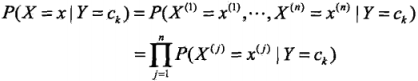
條件獨立假設等於是說用於分類的特徵在類確定的條件下都是條件獨立的，這一假設使樸素貝葉斯法變得簡單，但有時也會犧牲一些分類的準確率
2. 樸素貝葉斯法的策略
0x1：期望風險最小化 - 根據模型進行判斷預測過程
樸素貝葉斯法預測時將例項分到後驗概率最大的類中，這等價於期望風險最小化。假設選擇0-1損失函式： 
，這時，期望風險是：
。該式中期望是對聯合分佈P（X，Y）取得，而聯合概率分佈我們是未知的，因此取等價的後驗概率條件期望：
為了使期望風險最小化，只需對X = x逐個極小化，由此得到
等式推導的最後一步就是最後後驗概率的意思，由此，根據期望風險最小化準則就推匯出了等價的後驗概率最大化準則：
，這就是樸素貝葉斯法所採用的數學原理
0x2：經驗風險最小化 - 模型建立過程
當模型是條件概率分佈，損失函式對數損失函式時，經驗風險最小化就等價於極大似然估計
0x3：結構風險最小化 - 模型建立過程
當模型是條件概率分佈時、損失函式是對數損失函式時、模型複雜度由模型的先驗概率表示時，結構化風險最小化就等價於最大後驗概率估計
Relevant Link:
https://www.google.com.hk/url?sa=t&rct=j&q=&esrc=s&source=web&cd=1&cad=rja&uact=8&ved=0ahUKEwj8m-mjmrvVAhUBzIMKHWiqCIoQFgglMAA&url=https%3a%2f%2fzh%2ewikipedia%2eorg%2fzh-cn%2f%25E6%259C%25B4%25E7%25B4%25A0%25E8%25B4%259D%25E5%258F%25B6%25E6%2596%25AF%25E5%2588%2586%25E7%25B1%25BB%25E5%2599%25A8&usg=AFQjCNGICcTloX_Ty9_xQ06UnWbSWHkcWw
3. 樸素貝葉斯法的演算法 - 引數估計
樸素貝葉斯法的策略是最大後驗概率準則，但是為了能夠計算每個類的後驗概率，需要先得到聯合概率分佈的，而聯合概率分佈不能直接求得，我們需要應用一些演算法來輔助我們逼近這個結果
0x1: 極大似然估計
在樸素貝葉斯訓練學習過程中，學習本質上就是在估計和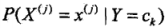
，可以應用極大似然估計法估計相應的概率
先驗概率的極大似然估計是：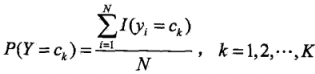
條件概率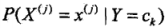的極大似然估計：實際場景中，輸入變數X可能是一個多維度特徵向量，因此設第j個特徵
可能取值的集合為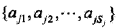
，條件概率
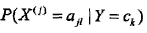的極大似然估計是：
，式中，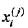
是第 i 個樣本的第 j 個特徵；
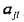是第 j 個特徵可能取的第 l 個值；I 為指示函式。
1. 極大似然引數的例子
我們先計算先驗概率：P（Y = 1） = 9 / 15；P（Y = -1） = 6 / 15
然後計算輸入變數各個特徵的條件概率：
= 2 / 9；
= 3 / 9；
= 4 / 9
= 1 / 9；
= 4 / 9；
= 4 / 9
= 3 / 6；
= 2 / 6；
= 1 / 6
= 3 / 6；
= 2 / 6；
= 1 / 6
根據最大後驗概率公式，對於給定的
，計算其最大後驗概率：
= 9 / 15 * 3 / 9 * 1 / 9 = 1 / 45
= 6 / 15 * 2 / 6 * 3 / 6 = 1 / 15
樸素貝葉斯法取後驗概率最大的對應的類，所以 y = -1
0x2: 貝葉斯估計 - 平滑化的極大似然估計
極大似然估計是一種單純從訓練樣本推導概率分佈的演算法，但是用極大似然估計可能會出現所要估計的概率值為0的情況（如果樣本數量不足，某些特徵在樣本中出現次數為0的時候，或者遇到樣本量不足導致預測偏差的情況），這時會影響聯合概率的估計，進一步影響後驗概率的計算結果，使分類產生偏差。解決這一問題的方法是採用貝葉斯估計（即加入平滑因子）
條件概率的貝葉斯估計公式：
，式中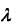
>=0，等價於在隨機變數各個取值的頻數上賦予一個正數
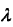>0，當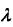
=0時公式退化到極大似然估計。通常取
=1，這時被稱為拉普拉斯平滑(Laplace smoothing)
先驗概率的貝葉斯估計是：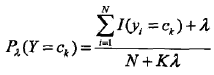
0x3：極大後驗概率估計（MAP） - 帶懲罰項的極大似然估計
引數估計演算法的另一個思路是MAP，我個人覺得它正好和貝葉斯估計反過來，即取Bayes估計中引數後驗分佈中概率最大的點來估計引數就是最大後驗估計，和極大似然估計最大的不同是：最大後驗估計的融入了要估計量的先驗分佈在其中。故最大後驗估計可以看做規則化的（帶懲罰項）最大似然估計 
對這個似然函式左右兩邊同時求log對數，對數函式是單調的，對最大估計無影響： 
等式最右邊第一項是標準的對數似然函式，第二項是先驗分佈的對數。這表明對引數的估計不再僅僅考慮樣本的統計結果，還要考慮進先驗分佈，它如同一個懲罰項。
Relevant Link:
http://blog.csdn.net/juanjuan1314/article/details/78189527?locationNum=4&fps=1 http://www.cnblogs.com/liliu/archive/2010/11/24/1886110.html
4. 樸素貝葉斯法的具體應用 - Spam fileter（垃圾分類demo）
0x1: 分類原理
我們知道，我們如果假設用於預測的所有詞(例如15個詞)互相之間都是有相關依存關係的，則樸素貝葉斯法的公式如下
但是了簡便實現，我們可以假設所有詞之間是互相獨立的，則計算過程會大大簡化
下面我們簡述原理與預測過程
1. 計算所有詞的 P(wordN | S)、以及 P(wordN | H)
1. 輸入所有郵件，然後得到郵件中每個單詞出現在垃圾郵件中的次數(條件概率 P(wordN | S) )，出現在正常郵件中的次數( P(wordN | H) ) 2. 設定預設概率，即如果在預測時遇到訓練語料庫中未見過的詞，則賦值預設概率例如: 3.7e-4 3. 先驗概率，設定Spam為0.2，Ham為0.8，即根據經驗，100封郵件裡有20封是垃圾郵件
有了這些引數，模型就訓練出來了。樸素貝葉斯分類器的訓練就是在計算條件概率
2. 預測新郵件，獲取所有關鍵字
然後輸入一封待處理郵件，找到裡面所有出現的關鍵詞
3. 計算獨立聯合條件概率
求出
，A為一封郵件是垃圾郵件的事件，T為關鍵詞出現在一封郵件中的事件。
是多個關鍵詞。A和T是關聯的事件。每個關鍵詞根據樸素貝葉斯的假設，是相互獨立的。
為這些關鍵詞同時出現的情況下A是垃圾郵件的概率。
代表了從待預測email中切出的詞，A代表Spam或者Ham，上面公式要分別計算A = S和A = H時的獨立聯合條件概率，在工程上也十分簡單，就是把每個詞在語料庫中出現的次數比例，累乘起來
有因為分母是已經確定的事實，概率乘積為1，可忽略
0x2: 利用樸素貝葉斯進行垃圾郵件分類 - 以單個詞為依據
我們用一個例子來說明樸素貝葉斯是怎麼應用在垃圾郵件分類中的
貝葉斯過濾器是一種統計學過濾器，建立在已有的統計結果之上。所以，我們必須預先提供兩組已經識別好的郵件，一組是正常郵件(ham)，另一組是垃圾郵件(spam)
我們用這兩組郵件，對過濾器進行"訓練"。這兩組郵件的規模越大，訓練效果就越好。這裡我們假設正常郵件和垃圾郵件各4000封
1. 訓練
"訓練"過程很簡單。首先，解析所有郵件，提取每一個詞(word)。然後，計算每個詞語在正常郵件和垃圾郵件中的出現頻率。比如，我們假定"sex"這個詞，在4000封垃圾郵件中，有200封包含這個詞，那麼它的spam出現頻率就是5%；而在4000封正常郵件中，只有2封包含這個詞，那麼ham出現頻率就是0.05%。（如果某個詞只出現在垃圾郵件中，就假定它在正常郵件的出現頻率是1%，反之亦然。這樣做是為了避免概率為0。隨著郵件數量的增加，計算結果會自動調整。）
有了這個初步的統計結果，過濾器就可以投入使用了
2. 概率計算
現在，我們收到了一封新郵件。在未經統計分析之前，我們假定它是垃圾郵件的概率為50%。（有研究表明，使用者收到的電子郵件中，80%是垃圾郵件。但是，這裡仍然假定垃圾郵件的"先驗概率"為50%。）
我們用S表示垃圾郵件（spam），H表示正常郵件（healthy）。因此，P(S)和P(H)的先驗概率，都是50%
然後，對這封郵件進行解析，發現其中包含了sex這個詞，請問這封郵件屬於垃圾郵件的概率有多高？
我們用W表示"sex"這個詞，那麼問題就變成了如何計算P(S|W)的值，即在某個詞語（W）已經存在的條件下，垃圾郵件（S）的概率有多大。
根據條件概率公式，馬上可以寫出
公式中，P(W|S)和P(W|H)的含義是，這個詞語在垃圾郵件和正常郵件中，分別出現的概率。這兩個值可以從歷史資料庫中得到，對sex這個詞來說，上文假定它們分別等於5%和0.05%。另外，P(S)和P(H)的值，前面說過都等於50%。所以，馬上可以計算P(S|W)的值：
因此，這封新郵件是垃圾郵件的概率等於99%。這說明，sex這個詞的推斷能力很強，將50%的"先驗概率"一下子提高到了99%的"後驗概率"
0x3: 利用樸素貝葉斯進行垃圾郵件分類 - 以多個詞為依據
在上面的例子中，基於一個詞就推斷一個email是否是垃圾郵件未免太過武斷，在實際使用中很容易出現誤報。因為在一封郵件裡往往會包含很多詞，為了能降低誤報。更實際的做法是選出這封信中P(S|W)最高的15個詞(對推斷共享最高的15個詞)，計算它們的聯合條件概率。如果有的詞是第一次出現則初始化為0.4，因為垃圾郵件使用的往往是固定的語句，如果出現了訓練庫中從未出現的詞，則有很大概率是正常的詞
而所謂聯合概率，就是指在多個事件發生的情況下，另一個事件發生概率有多大。比如，已知W1和W2是兩個不同的詞語，它們都出現在某封電子郵件之中，那麼這封郵件是垃圾郵件的概率，就是聯合概率。
在已知W1和W2的情況下，無非就是兩種結果：垃圾郵件（事件E1）或正常郵件（事件E2）
其中，W1、W2和垃圾郵件的概率分別如下：
如果假定所有事件都是獨立事件（這是一個強假設，可能會導致預測的準確性下降），那麼就可以計算P(E1)和P(E2)：
由於在W1和W2已經發生的情況下，垃圾郵件的概率等於下面的式子：
將上式帶入即
將先驗概率P(S)等於0.5代入，得到
將P(S|W1)記為P1，P(S|W2)記為P2，公式就變成
這就是聯合概率的計算公式，將情況從二詞擴充套件到15詞，最終公式為
0x4: 程式碼示例
# -*- coding: utf-8 -*- # for tokenize import nltk from nltk.corpus import stopwords from nltk.tokenize import wordpunct_tokenize # for reading all the files from os import listdir from os.path import isfile, join # add path to NLTK file nltk.data.path = ['nltk_data'] # load stopwords stopwords = set(stopwords.words('english')) # path for all the training data sets # 用於訓練模型的語料集 spam_path = 'data/spam/' easy_ham_path = 'data/easy_ham/' # change it to the type of mails you want to classify # path to the hard ham mails # 用於預測檢驗效果4個語料庫 spam2_path = 'data/spam_2/' easy_ham2_path = 'data/easy_ham_2/' hard_ham2_path = 'data/hard_ham_2/' hard_ham_path = 'data/hard_ham/' # 分別測試模型在4種不同型別的資料集中的分類效果 test_paths = [spam2_path, easy_ham2_path, hard_ham_path, hard_ham2_path] def get_words(message): """ Extracts all the words from the given mail and returns it as a set. """ # thanks http://slendermeans.org/ml4h-ch3.html # remove '=' symbols before tokenizing, since these # sometimes occur within words to indicate, e.g., line-wrapping # also remove newlines all_words = set(wordpunct_tokenize(message.replace('=\\n', '').lower())) # remove the stopwords msg_words = [word for word in all_words if word not in stopwords and len(word) > 2] return msg_words def get_mail_from_file(file_name): """ Returns the entire mail as a string from the given file. """ message = '' with open(file_name, 'r') as mail_file: for line in mail_file: # the contents of the actual mail start after the first newline # so find it, and then extract the words if line == '\n': # make a string out of the remaining lines for line in mail_file: message += line return message def make_training_set(path): """ Returns a dictionary of <term>: <occurrence> of all the terms in files contained in the directory specified by path. path is mainly directories to the training data for spam and ham folders. occurrence is the percentage of documents that have the 'term' in it. frequency is the total number of times the 'term' appears across all the documents in the path """ # initializations training_set = {} mails_in_dir = [mail_file for mail_file in listdir(path) if isfile(join(path, mail_file))] # count of cmds in the directory cmds_count = 0 # total number of files in the directory total_file_count = len(mails_in_dir) for mail_name in mails_in_dir: if mail_name == 'cmds': cmds_count += 1 continue # get the message in the mail message = get_mail_from_file(path + mail_name) # we have the message now # get the words in the message terms = get_words(message) # what we're doing is tabulating the number of files # that have the word in them # add these entries to the training set for term in terms: if term in training_set: training_set[term] = training_set[term] + 1 else: training_set[term] = 1 # reducing the count of cmds files from file count total_file_count -= cmds_count # calculating the occurrence for each term for term in training_set.keys(): training_set[term] = float(training_set[term]) / total_file_count return training_set # c is an experimentally obtained value # 貝葉斯估計P(S) = P(H) = 0.5 # 當一個新詞出現時，我們假定為3.7e-4 def classify(message, training_set, prior=0.5, c=3.7e-4): """ Returns the probability that the given message is of the given type of the training set. """ # 獲取word token list msg_terms = get_words(message) msg_probability = 1 for term in msg_terms: if term in training_set: msg_probability *= training_set[term] else: msg_probability *= c return msg_probability * prior spam_training_set, ham_training_set = {}, {} def trainingProess(): global spam_training_set, ham_training_set print 'Loading training sets...', spam_training_set = make_training_set(spam_path) ham_training_set = make_training_set(easy_ham_path) print 'done.' def testProcess(): global spam_training_set, ham_training_set SPAM = 'spam' HAM = 'ham' for mail_path in test_paths: mails_in_dir = [mail_file for mail_file in listdir(mail_path) if isfile(join(mail_path, mail_file))] results = {} results[SPAM] = 0 results[HAM] = 0 print 'Running classifier on files in', mail_path[5:-1], '...' for mail_name in mails_in_dir: if mail_name == 'cmds': continue # 獲取email的全文 mail_msg = get_mail_from_file(mail_path + mail_name) # 0.2 and 0.8 because the ratio of samples for spam and ham were the same # 貝葉斯估計P(S) = 0.2；P(H) = 0.8 # 當一個新詞出現時，我們假定為3.7e-4 spam_probability = classify(mail_msg, spam_training_set, 0.2) ham_probability = classify(mail_msg, ham_training_set, 0.8) # 計算得到獨立聯合條件概率: # P(T1|S) * P(T2|S) * ... * P(Tn|S) # P(T1|H) * P(T2|H) * ... * P(Tn|H) # 根據貝葉斯估計概率分別對S和H類的概率預測結果，判定屬於垃圾郵件還是正常郵件 if spam_probability > ham_probability: results[SPAM] += 1 else: results[HAM] += 1 total_files = results[SPAM] + results[HAM] spam_fraction = float(results[SPAM]) / total_files ham_fraction = 1 - spam_fraction print 'Fraction of spam messages =', spam_fraction print 'Fraction of ham messages =', ham_fraction print '' if __name__ == '__main__': # training process # 訓練模型，得到訓練集中每個詞的條件概率 trainingProess() # test process # 測試模型 testProcess() # 接收手工輸入，並基於當前模型判定是否是惡意郵件 mail_msg = raw_input('Enter the message to be classified:') print '' ## 0.2 and 0.8 because the ratio of samples for spam and ham were the 0.2-0.8 spam_probability = classify(mail_msg, spam_training_set, 0.2) ham_probability = classify(mail_msg, ham_training_set, 0.8) if spam_probability > ham_probability: print 'Your mail has been classified as SPAM.' else: print 'Your mail has been classified as HAM.' print ''
Relevant Link:
http://www.ganecheng.tech/blog/53219332.html https://en.wikipedia.org/wiki/Naive_Bayes_spam_filtering https://github.com/aashishsatya/Bayesian-Spam-Filter/blob/master/ClassifierDemo.py http://www.ganecheng.tech/blog/53219332.html https://github.com/dwhitena/bayes-spam-filter http://www2.aueb.gr/users/ion/data/enron-spam/ http://www.ruanyifeng.com/blog/2011/08/bayesian_inference_part_two.html http://www.voidcn.com/blog/win_in_action/article/p-5800906.html
Copyright (c) 2017 LittleHann All rights reserved