NLP相關問題中文字資料特徵表達初探

Andrew.Hann發表於2017-08-03

1. NLP問題簡介

0x1：NLP問題都包括哪些內涵

人們對真實世界的感知被成為感知世界，而人們用語言表達出自己的感知視為文字資料。那麼反過來，NLP，或者更精確地表達為文字挖掘，則是從文字資料出發，來儘可能復原人們的感知世界，從而表達真實世界的過程。這裡面就包括如圖中所示的模型和演算法，包括：

（1）文字層：NLP文字表示； 
（2）文字-感知世界：詞彙相關性分析、主題模型、意見情感分析等； 
（3）文字-真實世界：基於文字的預測等；

顯而易見，文字表示在文字挖掘中有著絕對核心的地位，是其他所有模型建構的基礎。

0x2：為什麼要進行文字表示

特徵提取的意義在於把複雜的資料，如文字和影象，轉化為數字特徵，從而在機器學習中使用。

在機器學習專案中，不管是純NLP問題還是NLP問題和非文字類混合資料的場景，我們都要面臨一個問題，如何將樣本集中的文字進行特徵表徵以及通過向量的方式表達出來。

這就要求我們對樣本的原始特徵空間進行抽象，將其對映到另一個向量化的定長特徵空間中，筆者在這篇blog中對常用的編碼和特徵工程方式進行一個梳理總結。

0x3：語言模型(Language Model, LM)

統計語言模型是詞序列的概率分佈，假設有一個 m 長度的文字序列，我們的目的是建立一個能夠描述給定詞序列對應的概率分佈。

掌握不同句子/片語的概率估計方法在NLP中有很多應用，特別是用來生成文字。語言模型在語音識別、機器翻譯、詞性標註、句法分析、手寫識別、資訊檢索都有廣泛的應用。

1. 語言模型的基礎模型 - 公式1

2. 目標函式（基於對數似然）

，其中C為語料，Context(w) 為詞 w 的上下文。

Relevant Link:

https://blog.csdn.net/tiffanyrabbit/article/details/72650606
https://blog.csdn.net/IT_bigstone/article/details/80739807
http://www.cnblogs.com/robert-dlut/p/4371973.html

2. 詞集模型 - 基於是否出現的one-hot思想的定長向量化表示，向量長度取決於詞集維度

詞集表示法和下個小節要介紹的詞袋模型在基本形式上類似的，都是對公式1 進行了極端地簡化，丟失了原始文字序列的序列資訊。

0x1：詞庫表示法

在train_x中，總共有6篇文件，每一行代表一個樣本即一篇文件。

我們的目標是將train_x轉化為可訓練矩陣，即生成每個樣本的詞向量。可以對train_x分別建立詞集模型來解決。

train_x = [["my", "dog", "has", "flea", "problems", "help", "please"],
               ["maybe", "not", "take", "him", "to", "dog", "park", "stupid"],
               ["my", "dalmation", "is", "so", "cute", "I", "love", "him"],
               ["stop", "posting", "stupid", "worthless", "garbage"],
               ["him", "licks", "ate", "my", "steak", "how", "to", "stop", "him"],
               ["quit", "buying", "worthless", "dog", "food", "stupid"]]

演算法步驟：

1）整合所有的單詞到一個集合中，假設最終生成的集合長度為wordSetLen = 31。
2）假設文件/樣本數為sampleCnt = 6，則建立一個sampleCnt * wordSetLen = 6 * 31的矩陣，這個矩陣被填入有效值之後，就是最終的可訓練矩陣m。
3）遍歷矩陣m，填入0,1有效值。0代表當前列的單詞沒有出現在當前行的樣本/文件中，1代表當前列的單詞出現在當前行的樣本/文件中。
4）最終生成一個6 * 31的可訓練矩陣。

讀者朋友需要知道的是，實際上，詞集模型的表徵能力比較弱，在實際的專案中非常少被使用到。

Relevant Link:

https://blog.csdn.net/zk_j1994/article/details/74780030

3. Bag Of Words（BOW）詞袋模型 - 基於詞頻統計的定長向量化表示，向量長度取決於詞集維度

詞袋模型，顧名思義，把各種詞放在一個文字的袋子裡，即把文字看做是無序的詞的組合。利用統計語言模型來理解詞序列的概率分佈。

文字中每個詞出現的概率僅與自身有關而無關於上下文。這是對公式1 的最極端的簡化，丟失了原始文字序列的序列資訊。

有一點需要讀者注意的是，語言模型與語言特徵提取演算法是兩個不同維度的概念，語言模型是一個框架，在一個具體的框架之下，存在不同的語言特徵提取和表徵演算法。

0x1：Bow模型的特點

1. 特點1：可以很容易得到一個定長的向量，不需要進行padding或者truncate處理；
2. 特點2：丟失了原始文字的序列依賴關係，在實際的專案中，讀者朋友還是需要仔細思考丟失了序列資訊對我們的最終特徵表達是否會有影響。
3. 針對特點3，筆者認為，並不說丟失序列關係是BOW模型的缺點，相反，世界上沒有絕對的優缺點，只有各具特點的演算法，某個特性是有點還是缺點，取決於應用的場景和我們對這個演算法的理解深刻程度。

0x2：詞庫表示法

1. 詞庫表示法的假設前提

對於一個文件（document），忽略其詞序、語法、句法，將其僅僅看做是一個詞集合，或者說是詞的一個組合，文件中每個詞的出現都是獨立的，不依賴於其他詞是否出，即假設這篇文章的作者在任意一個位置選擇一個詞彙都不受前面句子的影響而獨立選擇的。

這是一種非常強的假設，比馬爾科夫假設還要強。

詞庫模型可以看成是獨熱編碼的一種擴充套件，它為每個單詞建立一個特徵。

2. 詞庫表示法有效性的依據

詞庫模型依據是：存在類似單詞集合的文章的語義同樣也是類似的

詞庫模型可以通過有限的編碼資訊實現有效的文件分類和檢索。

3. 舉例說明詞庫表示法

1. 針對單個sentence文字進行編碼

假設我們有2段獨立的sentence

John likes to watch movies. Mary likes too.
John also likes to watch football games.

根據上述兩句話中出現的單詞, 我們能構建出一個無序字典 (dictionary)，字典的key是token化後的單詞，字典的value是該詞在字典中的索引，字典的length長度是10。

{"John": 1, "likes": 2, "to": 3, "watch": 4, "movies": 5, "also": 6, "football": 7, "games": 8, "Mary": 9, "too": 10}

# John出現了1次；like出現了2次；also沒出現

該字典中包含10個單詞, 每個單詞有唯一索引, 注意它們的順序和出現在句子中的順序沒有關聯。僅僅是是一個索引數字而已。

根據這個字典, 我們能將上述兩句話重新表達為下述兩個向量:

[1, 2, 1, 1, 1, 0, 0, 0, 1, 1]
[1, 1, 1, 1, 0, 1, 1, 1, 0, 0]

這兩個向量共包含10個元素, 其中第 i 個元素表示字典中第 i 個單詞在句子中出現的次數。

因此，BoW模型（詞庫表示法屬於Bow模型的一種）可認為是一種統計直方圖 (histogram)。

2. 針對包含多行sentence的document進行編碼

每個 document(文字) 可以被看做一個多元 sample(樣本)(特徵向量)。

還是上面的例子，假設我們有一個包含2段獨立的sentence的document

John likes to watch movies. Mary likes too.
John also likes to watch football games.

文字的集合可被表示為矩陣形式，每行一條文字，每列對應每個文字中出現的詞令牌(如單個詞)的頻率。

[
　　[1, 2, 1, 1, 1, 0, 0, 0, 1, 1],
　　[1, 1, 1, 1, 0, 1, 1, 1, 0, 0]
]

4. 詞庫表示法的sklearn封裝實現

sklearn對bag-of-word的詞頻向量化處理進行了封裝，scikit-learn為數值特徵提取最常見的方式提供了一系列工具

1. tokenizing: 對每個可能的詞令牌分成字串(word split)並賦予整形的id(索引化)，比如使用空格和作為令牌分割依據 
2. counting: 統計每個詞令牌在文件(單個文件，不是整體訓練集)中的出現次數 
3. normalizing: 在大多數的文件 / 樣本中，可以減少重要的次令牌的權重

CountVectorizer 在單個類中實現了令牌化和出現頻數統計:

令牌化字串，提取至少兩個字母的詞

from sklearn.feature_extraction.text import CountVectorizer
if __name__ == '__main__':
    vectorizer = CountVectorizer(min_df=1) 
        analyze = vectorizer.build_analyzer()
        print analyze("This is a text document to analyze.")
"" [u'this', u'is', u'text', u'document', u'to', u'analyze']

每個在擬閤中被分析器發現的詞被指派了一個獨一無二的索引，在結果矩陣中表示一列。對於列的翻譯可以被如下方式檢索

from sklearn.feature_extraction.text import CountVectorizer

if __name__ == '__main__':
    corpus = [
        'This is the first document.',
        'This is the second second document.',
        'And the third one.',
        'Is this the first document?',
    ]
    vectorizer = CountVectorizer(min_df=1)
    X = vectorizer.fit_transform(corpus)
    print vectorizer.get_feature_names()
    print X.toarray()

''''
[u'and', u'document', u'first', u'is', u'one', u'second', u'the', u'third', u'this']
總體樣本庫中共有9個token word

[[0 1 1 1 0 0 1 0 1]
 [0 1 0 1 0 2 1 0 1]
 [1 0 0 0 1 0 1 1 0]
 [0 1 1 1 0 0 1 0 1]]
每一行代表一個sentence，共4行(4個sentence)
每一列代表一個token詞的詞頻，共9列(9個token word)
''''

對執行的結果我們仔細觀察下，第一個sentence和最後一個文字sentence分別表達了陳述和疑問兩種句式(token word出現的位置不一樣，造成表達意思的不同)，但是因為它們包含的詞都相同。

但是進過詞袋編碼後，得到的特徵向量都是一樣的，很顯然，這個編碼過程丟失了這個疑問句的句式資訊，這就是詞袋模型最大的缺點：不能捕獲詞間相對位置資訊

'This is the first document.',
'Is this the first document?',

[[0 1 1 1 0 0 1 0 1] 
 [0 1 1 1 0 0 1 0 1]]

Relevant Link:

http://www.cnblogs.com/platero/archive/2012/12/03/2800251.html
http://feisky.xyz/machine-learning/resources/github/spark-ml-source-analysis/%E7%89%B9%E5%BE%81%E6%8A%BD%E5%8F%96%E5%92%8C%E8%BD%AC%E6%8D%A2/CountVectorizer.html

0x3：TF-IDF（Term Frequency-Inverse Document Frequency）表示法

TF-IDF(term frequency–inverse document frequency)是一種用於資訊檢索與資料探勘的常用加權技術。

TF-IDF產生的特徵向量是帶有傾向性的，主要可以被用以評估一字詞對於一個檔案集或一個語料庫中的其中一份檔案的重要程度。

字詞的重要性隨著它在檔案中出現的次數成正比增加，但同時會隨著它在語料庫中出現的頻率成反比下降。

TF-IDF屬於BOW語言模型的一種，但是在基礎的詞頻統計之上增加和單個詞和全域性詞集的相對關係。同時，TF-IDF也不關注詞序資訊，TF-IDF同樣也丟失了詞序列資訊。

1. TF-IDF的加權詞頻統計思想

用通俗的話總結TF-IDF的主要思想是：

如果某個詞或短語在一篇文章中出現的頻率TF高，並且在其他文章中很少出現，則認為此詞或者短語具有很好的類別區分能力，適合用來分類，也即可以作為所謂的關鍵字。

假定現在有一篇長文《中國的蜜蜂養殖》，我們準備用計算機提取它的關鍵詞，一個容易想到的思路，就是找到出現次數最多的詞。如果某個詞很重要，它應該在這篇文章中多次出現。

於是，我們進行"詞頻"（Term Frequency，縮寫為TF）統計。

在統計結束後我們會發現，出現次數最多的詞是 "的"、"是"、"在" 這一類最常用的詞。它們叫做"停用詞"(stop words)，在大多數情況下這對找到結果毫無幫助、我們採取過濾掉停用詞的策略。

假設我們把它們都過濾掉了，只考慮剩下的有實際意義的詞。這樣又會遇到了另一個問題，我們可能發現"中國"、"蜜蜂"、"養殖"這三個詞的出現次數一樣多。這是不是意味著，作為關鍵詞，它們的重要性是一樣的？

顯然不是這樣。因為"中國"是很常見的詞(在日常的語料庫中出現頻率較高)，相對而言，"蜜蜂"和"養殖"不那麼常見(傾向於專有領域的詞)。

如果這三個詞在一篇文章的出現次數一樣多，有理由認為，"蜜蜂"和"養殖"的重要程度要大於"中國"，也就是說，在關鍵詞排序上面，"蜜蜂"和"養殖"應該排在"中國"的前面。所以，我們需要一個重要性調整係數，衡量一個詞是不是常見詞。如果某個詞比較少見，但是它在這篇文章中多次出現，那麼它很可能就反映了這篇文章的特性，正是我們所需要的關鍵詞

用統計學語言表達，就是在詞頻的基礎上，要對每個詞分配一個"重要性"權重

1. 最常見的詞("的"、"是"、"在")給予最小的權重；
2. 較常見的詞("中國")給予較小的權重；
3. 較少見的詞("蜜蜂"、"養殖")給予較大的權重；

這個權重叫做"逆文件頻率"（Inverse Document Frequency，縮寫為IDF），它的大小與一個詞的常見程度成反比，它的作用是對原始詞頻權重進行反向調整。

知道了"詞頻"（TF）和"逆文件頻率"（IDF）以後，將這兩個值相乘，就得到了一個詞的TF-IDF值。某個詞對文章的重要性越高，它的TF-IDF值就越大。所以，排在最前面的幾個詞，就是這篇文章的關鍵詞

2. TF-IDF演算法流程

第一步 - 計算詞頻

考慮到文章有長短之分，為了便於不同文章的比較，進行"詞頻"歸一化"

第二步 - 計算逆文件頻率

這時，需要一個語料庫（corpus），用來模擬語言的總體使用環境

如果一個詞越常見，那麼分母就越大，逆文件頻率就越小越接近0。分母之所以要加1，是為了避免分母為0（即所有文件都不包含該詞），log表示對得到的值取對數。

第三步 - 計算TF-IDF

可以看到，TF-IDF與一個詞在文件中的出現次數成正比，與該詞在整個語言中的出現次數成反比

以《中國的蜜蜂養殖》為例：

假定該文長度為1000個詞，"中國"、"蜜蜂"、"養殖"各出現20次，則這三個詞的"詞頻"（TF）都為0.02。然後，搜尋Google發現，包含"的"字的網頁共有250億張，假定這就是中文網頁總數包含"中國"的網頁共有62.3億張；包含"蜜蜂"的網頁為0.484億張；包含"養殖"的網頁為0.973億張。

則它們的逆文件頻率（IDF）和TF-IDF如下

中國
IDF = math.log(250 / 63.3) = 1.37357558871
TF-IDF = IDF * 0.02 = 0.0274715117742

蜜蜂
IDF = math.log(250 / 63.3) = 5.12671977312 
TF-IDF = IDF * 0.02 = 0.102534395462

養殖
IDF = math.log(250 / 63.3) = 4.84190569082 
TF-IDF = IDF * 0.02 = 0.0968381138164

從上表可見，"蜜蜂"的TF-IDF值最高，"養殖"其次，"中國"最低。所以，如果只選擇一個詞，"蜜蜂"就是這篇文章的關鍵詞

3. TF-IDF的sklearn封裝實現

因為 tf–idf 在特徵提取中經常被使用，所以有一個類: TfidfVectorizer 在單個類中結合了所有類和類中的選擇:

from sklearn.feature_extraction.text import TfidfVectorizer

if __name__ == '__main__':
    corpus = [
        'This is the first document.',
        'This is the second second document.',
        'And the third one.',
        'Is this the first document?',
    ]
    vectorizer = TfidfVectorizer(min_df=1)
    tfidf = vectorizer.fit_transform(corpus)
    print vectorizer.vocabulary_
    print tfidf.toarray()
''''

{u'and': 0, u'third': 7, u'this': 8, u'is': 3, u'one': 4, u'second': 5, u'the': 6, u'document': 1, u'first': 2}
[[ 0.          0.43877674  0.54197657  0.43877674  0.          0.        0.35872874  0.          0.43877674]
 [ 0.          0.27230147  0.          0.27230147  0.          0.85322574    0.22262429  0.          0.27230147]
 [ 0.55280532  0.          0.          0.          0.55280532  0.        0.28847675  0.55280532  0.        ]
 [ 0.          0.43877674  0.54197657  0.43877674  0.          0.        0.35872874  0.          0.43877674]]

可以看到，document在整個語料庫中都出現，所以權重被動態降低了

Relevant Link:

http://www.ruanyifeng.com/blog/2013/03/tf-idf.html
http://www.cnblogs.com/ybjourney/p/4793370.html
http://www.cc.ntu.edu.tw/chinese/epaper/0031/20141220_3103.html
https://nlp.stanford.edu/IR-book/html/htmledition/tf-idf-weighting-1.html
http://sklearn.lzjqsdd.com/modules/feature_extraction.htm

0x4：LSA（Latent Semantic Analysis）潛在語義分析表示法

筆者思考：LSA並不單純地像詞庫表示法和TF-IDF一樣，僅僅進行文件的向量化表徵。相比之下，LSA演算法在傳統詞頻統計語言模型之上進行了語義分析。所以，嚴格來說，LSA可能並不能算是一個單純的文字特徵表徵法，LSA產出的是包含語義特性的向量特徵表徵。

1. LSA是什麼

潛在語義分析LSA（Latent Semantic Analysis ）也叫作潛在語義索引LSI（ Latent Semantic Indexing ）顧名思義是通過分析文章（documents ）來挖掘文章的潛在意思或語義（concepts ）。

不同的單詞可以表示同一個語義，或一個單詞同時具有多個不同的意思，這些的模糊歧義是LSA主要解決的問題。

例如，bank 這個單詞如果和mortgage, loans, rates 這些單詞同時出現時，bank 很可能表示金融機構的意思。可是如果bank 這個單詞和lures, casting, fish一起出現，那麼很可能表示河岸的意思。

2. LSA的基本假設

一篇文章（包含很多sentence的document）可以隨意地選擇各種單詞來表達，因此不同的作者的詞語選擇風格都大不相同，表達的語義也因此變得模糊。

這種單詞選擇的隨機性必然將噪聲的引入到“單詞-語義關係”（word-concept relationship）。

LSA能過濾掉一些噪聲，同時能在語料庫中找出一個最小的語義子集（ to find the smallest set of concepts that spans all the documents）。所以本質上LSA也可以理解為一種資訊壓縮的演算法。

LSA引入了一些重要的假設

1. 文章通過”bags of words”詞頻語言模型的形式來表示，也就是說單詞的出現順數並不重要，而與單詞在文中出現的次數相關
2. 語義通過“一組”最有可能同時出現的單詞來表示。例如”leash”, “treat”, “obey” 常出現在關於 dog training的文章裡面，一組單詞共同決定了一種語義。
3. 每個單詞假設只有一個意思，當然這個假設在遇到““banks””（既表示河岸也表示金融銀行）這種情況當然不合適，但是這個假設將有助於簡化問題難度。

3. LSA的工作原理

1）詞-文件矩陣（Occurences Matrix) - 將原始document轉換為詞頻統計稀疏矩陣

LSA 使用詞-文件矩陣來描述一個詞語是否在一篇文件中。

詞-文件矩陣式一個稀疏矩陣，其行代表詞語，其列代表文件。

一般情況下，詞-文件矩陣的元素是該詞在文件中的出現次數（詞庫表示法），也可以是是該詞語的TF-IDF。詞-文件矩陣的本質就是傳統的詞頻語言模型，後面的LSA語義分析在基於傳統的詞頻語言模型進行了擴充。

2）SVD奇異值矩陣分解 - 降維

在構建好詞-文件矩陣之後，LSA將對該矩陣進行降維，來找到詞-文件矩陣的一個低階近似。降維的原因有以下幾點：

1. 原始的詞-文件矩陣太大導致計算機無法處理，從此角度來看，降維後的新矩陣式原有矩陣的一個近似；
2. 原始的詞-文件矩陣中有噪音，從此角度來看，降維後的新矩陣式原矩陣的一個去噪矩陣，即冗餘資訊壓縮；
3. 原始的詞-文件矩陣過於稀疏。原始的詞-文件矩陣精確的反映了每個詞是否“出現”或“出現的頻次”於某篇文件的情況，然而我們往往對某篇文件“相關”的所有詞更感興趣，因此我們需要發掘一個詞的各種同義詞的情況；
4. 將維可以解決一部分同義詞的問題，也能解決一部分二義性問題。具體來說，原始詞-文件矩陣經過降維處理後，原有詞向量對應的二義部分會加到和其語義相似的詞上，而剩餘部分則減少對應的二義分量；

降維的結果是不同的詞或因為其語義的相關性導致合併，如下面將car和truck進行了合併：

{(car), (truck), (flower)} --> {(1.3452 * car + 0.2828 * truck), (flower)}

3）SVD降維推導

假設 X 矩陣是詞-文件矩陣，其元素（i，j）代表詞語 i 在文件 j 中的出現次數，則 X矩陣看上去是如下的樣子：

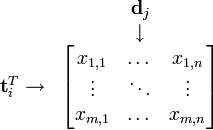
$\begin{matrix} & \textbf{d}_j \\ & \downarrow \\\textbf{t}_i^T \rightarrow &\begin{bmatrix} x_{1,1} & \dots & x_{1,n} \\\vdots & \ddots & \vdots \\x_{m,1} & \dots & x_{m,n} \\\end{bmatrix}\end{matrix}$

可以看到，每一行代表一個詞的向量，該向量描述了該詞和所有文件的關係。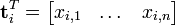 $\textbf{t}_i^T = \begin{bmatrix} x_{i,1} & \dots & x_{i,n} \end{bmatrix}$

相似的，一列代表一個文件向量，該向量描述了該文件與所有詞的關係。 $\textbf{d}_j = \begin{bmatrix} x_{1,j} \\ \vdots \\ x_{m,j} \end{bmatrix}$

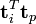詞向量 $\textbf{t}_i^T \textbf{t}_p$ 的點乘可以表示這兩個單詞在文件集合中的相似性。矩陣 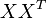$X X^T$ 包含所有詞向量點乘的結果，元素（i，p）和元素（p，i）具有相同的值，代表詞 p 和詞 i 的相似度。

類似的，矩陣 $X^T X$ 包含所有文件向量點乘的結果，也就包含了所有文件總體的相似度。

現在假設存在矩陣 $X$ 的一個分解，即矩陣 $X$ 可分解成正交矩陣U和V，和對角矩陣 $\Sigma$ 的乘積。

這種分解叫做奇異值分解（SVD），即：

$\begin{matrix}X = U \Sigma V^T\end{matrix}$

因此，詞與文字的相關性矩陣可以表示為：

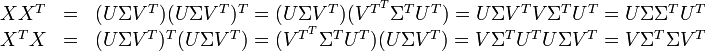
$\begin{matrix}X X^T &=& (U \Sigma V^T) (U \Sigma V^T)^T = (U \Sigma V^T) (V^{T^T} \Sigma^T U^T) = U \Sigma V^T V \Sigma^T U^T = U \Sigma \Sigma^T U^T \\X^T X &=& (U \Sigma V^T)^T (U \Sigma V^T) = (V^{T^T} \Sigma^T U^T) (U \Sigma V^T) = V \Sigma^T U^T U \Sigma V^T = V \Sigma^T \Sigma V^T\end{matrix}$

因為

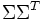\Sigma \Sigma^T

與

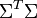\Sigma^T \Sigma

是對角矩陣，因此

U

肯定是由

X X^T

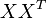的特徵向量組成的矩陣，同理

V

是

X^T X

特徵向量組成的矩陣。這些特徵向量對應的特徵值即為

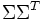\Sigma \Sigma^T

中的元素。綜上所述，這個分解看起來是如下的樣子：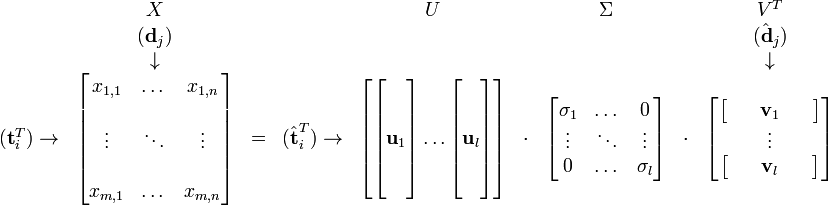

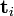\begin{matrix} & X & & & U & & \Sigma & & V^T \\ & (\textbf{d}_j) & & & & & & & (\hat{\textbf{d}}_j) \\ & \downarrow & & & & & & & \downarrow \\(\textbf{t}_i^T) \rightarrow &\begin{bmatrix} x_{1,1} & \dots & x_{1,n} \\\\\vdots & \ddots & \vdots \\\\x_{m,1} & \dots & x_{m,n} \\\end{bmatrix}&=&(\hat{\textbf{t}}_i^T) \rightarrow&\begin{bmatrix} \begin{bmatrix} \, \\ \, \\ \textbf{u}_1 \\ \, \\ \,\end{bmatrix} \dots\begin{bmatrix} \, \\ \, \\ \textbf{u}_l \\ \, \\ \, \end{bmatrix}\end{bmatrix}&\cdot&\begin{bmatrix} \sigma_1 & \dots & 0 \\\vdots & \ddots & \vdots \\0 & \dots & \sigma_l \\\end{bmatrix}&\cdot&\begin{bmatrix} \begin{bmatrix} & & \textbf{v}_1 & & \end{bmatrix} \\\vdots \\\begin{bmatrix} & & \textbf{v}_l & & \end{bmatrix}\end{bmatrix}\end{matrix}

\sigma_1, \dots, \sigma_l

被稱作是奇異值，而

u_1, \dots, u_l

和

v_1, \dots, v_l

則叫做左奇異向量和右奇異向量。

通過矩陣分解可以看出，原始矩陣中的

\textbf{t}_i

只與U矩陣的第 i 行有關，我們則稱第 i 行為

\hat{\textrm{t}}_i

。

同理，原始矩陣中的

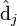\hat{ \textrm{d}}_j

只與

V^T

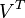中的第 j 列有關，我們稱這一列為

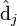\hat{ \textrm{d}}_j

。

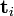\textbf{t}_i

與

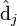\hat{ \textrm{d}}_j

並非特徵值，但是其由矩陣所有的特徵值所決定。

當我們選擇 k 個最大的奇異值，和它們對應的Ｕ與Ｖ中的向量相乘，則能得到一個X矩陣的 k 階近似，此時該矩陣和X矩陣相比有著最小誤差（即殘差矩陣的Frobenius範數）。

但更有意義的是這麼做可以將詞向量和文件向量對映到語義空間。

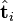向量 $\hat{\textbf{t}}_i$ 與含有 k 個奇異值的矩陣相乘，實質是從高維空間到低維空間的一個變換，可以理解為是一個高維空間到低維空間的近似。

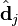同理，向量 $\hat{\textbf{d}}_j$ 也存在這樣一個從高維空間到低維空間的變化。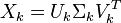

這種變換用公式總結出來就是這個樣子： $X_k = U_k \Sigma_k V_k^T$

4. LSA的應用

在低維語義空間可對文件進行比較，進而可用於文件聚類和文件分類。
在翻譯好的文件上進行訓練，可以發現不同語言的相似文件，可用於跨語言檢索。
發現詞與詞之間的關係，可用於同義詞、歧義詞檢測。.
通過查詢對映到語義空間，可進行資訊檢索。
從語義的角度發現詞語的相關性，可用於“選擇題回答模型”（multi choice qustions answering model）。

5. LSA演算法侷限性

新生成的矩陣的解釋性比較差。造成這種難以解釋的結果是因為SVD只是一種數學變換，並無法對應成現實中的概念。

LSA無法撲捉一詞多意的現象。在原始詞-向量矩陣中，每個文件的每個詞只能有一個含義。比如同一篇文章中的“The Chair of Board"和"the chair maker"的chair會被認為一樣。在語義空間中，含有一詞多意現象的詞其向量會呈現多個語義的平均。相應的，如果有其中一個含義出現的特別頻繁，則語義向量會向其傾斜。

LSA具有詞袋模型的缺點，即在一篇文章，或者一個句子中忽略詞語的先後順序。

LSA的概率模型假設文件和詞的分佈是服從聯合正態分佈的，但從觀測資料來看是服從泊松分佈的。因此LSA演算法的一個改進PLSA使用了多項分佈，其效果要好於LSA。

0x5：在實際專案中需要注意的點

1. 詞袋模型編碼後的詞向量 padding or truncating

詞袋模型編碼得到的詞向量長度，等於詞袋中詞集的個數。

然而，通常在一個海量的document集合中，詞集的個數是非常巨大的。如果全部都作為詞集，那麼最終編碼得到的詞向量會非常巨大，同時也很容易遇到稀疏問題。

因此，我們一般需要在特徵編碼前進行padding or truncating，具體的做法可以由以下兩種：

1. 根據TOP Order排序獲取指定數量的詞集，例如取 top 8000高頻詞作為詞集；
2. 針對編碼後得到的詞向量進行 padding or truncating

這兩種做法的最終效果是一樣的。

Relevant Link:

https://blog.csdn.net/roger__wong/article/details/41175967
https://blog.csdn.net/zhzhji440/article/details/47193731

4. N-Gram語言模型 - 一種多片語合語言模型

0x1：N-Gram演算法思想

1. 完整序列語言模型存在的問題

我們回想公式1，語言模型序列假設：第n個詞的出現只與前面N-1個詞相關，而與其它任何詞都不相關，整句的概率就是各個詞出現概率的乘積。

這種模型雖然非常合理（對真實情況的模擬逼近），但是存在兩個比較嚴重的缺陷

1. 一個缺陷是引數空間過大，不可能實用化，一個序列長度為N的引數個數為: N!
2. 另外一個缺陷是資料稀疏嚴重，越長的序列的越不容易出現，整個引數矩陣上會有很多0值

2. Ngram（N元模型）- 馬爾科夫有限詞序列依賴假設

為了解決上一小節提到的2個缺陷，我們引入另一個近似模型：馬爾科夫假設，一個詞的出現僅僅依賴於它前面出現的有限的一個或者幾個詞，這種模型就大大減少了需要參與計算的先驗引數。

例如，如果一個詞的出現僅依賴於它前面出現的一個詞，那麼我們就稱之為 bigram(2-gram)

P(T) = P(W1W2W3…Wn)=P(W1)P(W2|W1)P(W3|W1W2)…P(Wn|W1W2…Wn-1)
≈P(W1)P(W2|W1)P(W3|W2)…P(Wn|Wn-1)

0x2：N-gram語言模型下的詞序特徵表徵方法

Ngram和BOW模型的區別就在於，對原始語言模型公式1 的假設簡化程度不同，Ngram保留了有限長度的序列資訊。除此之外，Ngram也同樣可以應用詞庫表示法、以及TF-IDF等表示法。

0x3：基於n-gram的機器學習應用

我們已經瞭解了n-gram的詞頻生成方法以及sentence概率估計原理，接下來看看n-gram可以用在哪些實際的場景中

1. 基於Ngram模型定義的字串距離

模糊匹配的關鍵在於如何衡量兩個長得很像的單詞(或字串)之間的“差異”，這種差異通常又稱為“距離”。除了可以定義兩個字串之間的編輯距離(通常利用Needleman-Wunsch演算法或Smith-Waterman演算法)，還可以定義它們之間的Ngram距離。

假設有一個字串S，那麼該字串的Ngram就表示按長度N切分原sentence得到的詞段(長度為N)，也就是S中所有長度為N的子字串。設想如果有兩個字串，然後分別求它們的Ngram，那麼就可以從它們的共有子串的數量這個角度去定義兩個字串間的Ngram距離。但是僅僅是簡單地對共有子串進行計數顯然也存在不足，這種方案顯然忽略了兩個字串長度差異可能導致的問題。比如字串girl和girlfriend，二者所擁有的公共子串數量顯然與girl和其自身所擁有的公共子串數量相等，但是我們並不能據此認為girl和girlfriend是兩個等同的匹配。為了解決該問題，有研究員提出以非重複的Ngram分詞為基礎來定義Ngram距離，公式表示如下：

|GN(S1)|+|GN(S2)|−2×|GN(S1)∩GN(S2)|

此處， $| G_{N} (S_{1}) |$

Go or rb ba ac ch he ev
Go or rb be ec ch hy yo ov

結合上面的公式，即可算得兩個字串之間的距離是8 + 9 − 2 × 4 = 9。顯然，字串之間的距離越小，它們就越接近。當兩個字串完全相等的時候，它們之間的距離就是0。可以看到，這種公式充分考慮到了字串的長度區別和相同片語2者的共同作用

2. 利用Ngram模型評估語句是否合理

從統計的角度來看，自然語言中的一個句子S可以由任何詞串構成，不過概率P(S)有大有小。例如：

S1 = 我剛吃過晚飯
S2 = 剛我過晚飯吃

顯然，對於中文而言S1是一個通順而有意義的句子，而S2則不是，所以對於中文來說P(S1)>P(S2)

假設我們現在有一個語料庫如下，其中<s1><s2>是句首標記，</s2></s1>是句尾標記：

<s1><s2>yes no no no no yes</s2></s1>
<s1><s2>no no no yes yes yes no</s2></s1>

下面我們的任務是來評估如下這個句子的概率：

<s1><s2>yes no no yes</s2></s1>

我們利用trigram來對這句話進行片語分解

所以我們要求的概率就等於： $1 / 2 \times 1 \times 1 / 2 \times 2 / 5 \times 1 / 2 \times 1 = 0.05$

3. 基於Ngram模型的文字分類器

Ngram如何用作文字分類器的呢？只要根據每個類別的語料庫訓練各自的語言模型，實質上就是每一個類別都有一個概率分佈，當新來一個文字的時候，只要根據各自的語言模型，計算出每個語言模型下這篇文字的發生概率，文字在哪個模型的概率大，這篇文字就屬於哪個類別了！

4. spam filtering

基於n-gram進行垃圾郵件判斷我理解本質上就是在進行文字分類，通過訓練"good email"和"spam email"的n-gram詞頻表，對新來的email分別根據2個詞頻表計算最大似然概率，根據得出概率最大的那個詞頻表判斷該email屬於哪一類

0x4：sklearn封裝實現

from sklearn.feature_extraction.text import CountVectorizer

if __name__ == '__main__':
    corpus = [
        'This is the first document.',
        'This is the second second document.',
        'And the third one.',
        'Is this the first document?',
    ]
    bigram_vectorizer = CountVectorizer(ngram_range=(1, 2), token_pattern=r'\b\w+\b', min_df = 1)
    X_2 = bigram_vectorizer.fit_transform(corpus).toarray()
    print X_2
    print bigram_vectorizer.vocabulary_
'''' 
[[0 0 1 1 1 1 1 0 0 0 0 0 1 1 0 0 0 0 1 1 0]
 [0 0 1 0 0 1 1 0 0 2 1 1 1 0 1 0 0 0 1 1 0]
 [1 1 0 0 0 0 0 0 1 0 0 0 1 0 0 1 1 1 0 0 0]
 [0 0 1 1 1 1 0 1 0 0 0 0 1 1 0 0 0 0 1 0 1]]
{u'and': 0, u'the second': 14, u'is': 5, u'this the': 20, u'one': 8, u'and the': 1, u'second': 9, u'first document': 4, u'is the': 6, u'second document': 10, u'the third': 15, u'document': 2, u'the first': 13, u'is this': 7, u'third': 16, u'this': 18, u'second second': 11, u'third one': 17, u'the': 12, u'this is': 19, u'first': 3}

上面輸入的結果，我們看第一行的前3個：0 0 1；0號index代表and，1號index代表and the，2號index代表document，0和1號索引都在第一個sentence裡未出現，所以g-gram之後的one-hot vector填0，而document出現在第一個sentence的最後一個位置，故填1，可見n-gram並不關注詞在樣本中的具體位置。n-gram保留的詞序列只是它自己的context上下文的片語序列

因為n-gram進行了N*N無序組合(用one-hot的思想抽象成了一個定長的vector)，因此向量化提取的詞因此變得很大，同時可以在定位模式時消歧義，同時我們注意到，n-gram本質上還是一種bag-of-words模型，因此n-gram編碼後的vector丟失了原始sentence的序列，它只儲存了N子序列的片語關係

Relevant Link:

http://blog.csdn.net/lengyuhong/article/details/6022053
https://flystarhe.github.io/2016/08/16/ngram/
http://blog.csdn.net/baimafujinji/article/details/51281816
https://en.wikipedia.org/wiki/Bag-of-words_model
http://www.52nlp.cn/tag/n-gram
https://blog.csdn.net/tiffanyrabbit/article/details/72650606

5. 基於詞袋對原始序列進行數值編碼 - 向量維度取決於原始序列長度

這種方法借鑑了詞袋模型的思想，使用生成的詞彙表對原始的詞序列進行逐個編碼，編碼後的詞序列長度和原始序列是一樣的。

之後為了輸入神經網路網路進行計算，常常使用padding或者truncating進行長度規範化。

基於keras進行一個簡單code example，說明該編碼方式：

import keras.preprocessing.text as T
from keras.preprocessing.text import Tokenizer

text1='some thing to eat'
text2='some thing to drink'
texts=[text1,text2]

print T.text_to_word_sequence(text1)  #['some', 'thing', 'to', 'eat']
print T.one_hot(text1,10)  #[7, 9, 3, 4]
print T.one_hot(text2,10)  #[7, 9, 3, 1]

tokenizer = Tokenizer(num_words=10)
tokenzier.fit_on_text(texts)
print tokenizer.word_count #[('some', 2), ('thing', 2), ('to', 2), ('eat', 1), ('drink', 1)]
print tokenizer.word_index #{'some': 1, 'thing': 2,'to': 3 ','eat': 4, drink': 5}
print tokenizer.word_docs #{'some': 2, 'thing': 2, 'to': 2, 'drink': 1,  'eat': 1}
print tokenizer.index_docs #{1: 2, 2: 2, 3: 2, 4: 1, 5: 1}

print tokenizer.text_to_sequences(texts) #[[1, 2, 3, 4], [1, 2, 3, 5]]
print tokenizer.text_to_matrix(texts) #
[[ 0.,  1.,  1.,  1.,  1.,  0.,  0.,  0.,  0.,  0.],
 [ 0.,  1.,  1.,  1.,  0.,  1.,  0.,  0.,  0.,  0.]]

這種NLP特徵提取方式的好處是避免因為原始資料被轉換到詞袋特徵空間過程中的資訊過度丟失，更多地保留了原始序列的上下文資訊。

Relevant Link:

https://keras-cn.readthedocs.io/en/latest/legacy/preprocessing/sequence/
https://blog.csdn.net/zzulp/article/details/76146947

6. RNN/LSTM - 長序列語言模型

RNN/LSTM是非詞頻統計型的語言模型。

7. Emberding詞向量空間表示法 - 向量長度取決於嵌入空間的維度

8. AutoEncodder - 基於深度神經網路隱藏層的資訊壓縮的特徵提取能力得到詞序列特徵表示

（未完待續）

特徵選擇和特徵生成問題初探
2018-07-29
特徵
資料庫事物相關問題
2020-09-20
資料庫
關於表資料行統計的問題和相關誤區
2011-06-18
表單資料相關
2016-01-04
特徵工程之特徵表達
2021-09-09
特徵工程
BIP Schedule相關資料表
2012-07-16
【資源】NLP 演算法工程師相關的面試題
2020-04-06
演算法工程師面試題
網站資料分析：資料倉儲相關的問題（三）
2014-06-07
網站
FI-AA相關資料表
2011-01-18
nlp中文字輸入的資料預處理方式
2024-08-09
Docker 相關問題
2022-06-07
Docker
django相關問題
2024-07-08
Django
electron相關問題
2024-07-12
使用全表掃描快取大表的相關問題
2013-02-18
快取
NLP相關論文綜述
2018-11-26
達夢資料庫手工恢復相關命令
2021-08-21
資料庫
請教一個資料表關係的問題
2003-08-01
JavaScript變數，資料和記憶體的相關問題
2020-09-25
JavaScript變數記憶體
Java相關問題整理
2018-12-29
Java
PHP相關問題集合
2017-11-16
PHP
大模型相關問題
2024-08-17
大模型
oracle變異表觸發器相關問題解決
2009-08-17
Oracle觸發器
mysql相關問題總結
2020-09-06
MySql
個人專案相關問題
2020-09-24
Sql Mode及相關問題
2015-09-23
SQL
Oracle MTS的相關問題
2010-07-06
Oracle
RUST所有權相關問題
2024-10-03
Rust
瀏覽器相關問題
2024-04-15
瀏覽器
python pip相關問題
2024-05-30
Python
replace()方法的正則表達相關應用
2017-02-10
關於盒模型相關的問題
2019-02-23
模型
關於 go-micro 相關問題
2021-06-28
Go
資料結構 - 雜湊表，初探
2024-10-27
資料結構
資料庫關聯問題
2007-04-14
資料庫
VMLogin 指紋與瀏覽器資料同步相關問題解析
2020-10-13
瀏覽器
關於資料庫表記錄主鍵生成的問題？
2003-03-19
資料庫
初學者 | NLP相關任務簡介
2019-08-30
資料庫相關
2017-09-13
資料庫

NLP相關問題中文字資料特徵表達初探

1. NLP問題簡介

0x1：NLP問題都包括哪些內涵

0x2：為什麼要進行文字表示

0x3：語言模型(Language Model, LM)

1. 語言模型的基礎模型 - 公式1

2. 目標函式（基於對數似然）

2. 詞集模型 - 基於是否出現的one-hot思想的定長向量化表示，向量長度取決於詞集維度

0x1：詞庫表示法

3. Bag Of Words（BOW）詞袋模型 - 基於詞頻統計的定長向量化表示，向量長度取決於詞集維度

0x1：Bow模型的特點

0x2：詞庫表示法

1. 詞庫表示法的假設前提

2. 詞庫表示法有效性的依據

3. 舉例說明詞庫表示法

1. 針對單個sentence文字進行編碼

2. 針對包含多行sentence的document進行編碼

4. 詞庫表示法的sklearn封裝實現

0x3：TF-IDF（Term Frequency-Inverse Document Frequency）表示法

1. TF-IDF的加權詞頻統計思想

2. TF-IDF演算法流程

第一步 - 計算詞頻

第二步 - 計算逆文件頻率

第三步 - 計算TF-IDF

3. TF-IDF的sklearn封裝實現

0x4：LSA（Latent Semantic Analysis）潛在語義分析表示法

1. LSA是什麼

2. LSA的基本假設

3. LSA的工作原理

1）詞-文件矩陣（Occurences Matrix) - 將原始document轉換為詞頻統計稀疏矩陣

2）SVD奇異值矩陣分解 - 降維

3）SVD降維推導

4. LSA的應用

5. LSA演算法侷限性

0x5：在實際專案中需要注意的點

1. 詞袋模型編碼後的詞向量 padding or truncating

4. N-Gram語言模型 - 一種多片語合語言模型

0x1：N-Gram演算法思想

1. 完整序列語言模型存在的問題

2. Ngram（N元模型）- 馬爾科夫有限詞序列依賴假設

0x2：N-gram語言模型下的詞序特徵表徵方法

0x3：基於n-gram的機器學習應用

1. 基於Ngram模型定義的字串距離

2. 利用Ngram模型評估語句是否合理

3. 基於Ngram模型的文字分類器

4. spam filtering

0x4：sklearn封裝實現

5. 基於詞袋對原始序列進行數值編碼 - 向量維度取決於原始序列長度

6. RNN/LSTM - 長序列語言模型

7. Emberding詞向量空間表示法 - 向量長度取決於嵌入空間的維度

8. AutoEncodder - 基於深度神經網路隱藏層的資訊壓縮的特徵提取能力得到詞序列特徵表示

相關文章