今天學習的是第6章,關於詞項權重方面的,重要性還是很大的。在電商搜尋應用中,用到這的地方很多。比如我們搜尋商品時,商品的屬性很多,如“標題”,“描述”。我們要匹配的關鍵字只要滿足這些屬性之一就返回,這時候我們一般對不同屬性不會一視同仁,比如“標題”中匹配的重要性就要比“描述”內容更大,更應該排在前面返回。
假設我們現在做一個線上電商的專案,商品有兩個屬性欄位,分別是“標題(title)”和“描述(desc)”,還是跟之前一樣我們可以寫出如下的倒排表:
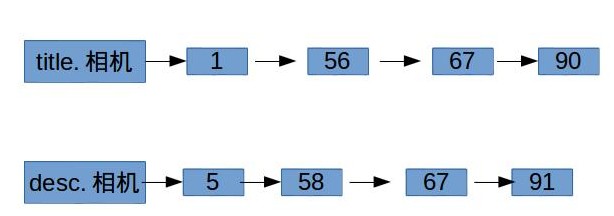
有了如上結構的倒排表,可以通過布林函式來查詢兩個欄位的組合查詢,比如“標題中包含相機或者描述中包含單反”的所有商品。上述倒排表把每個欄位屬性當成一個獨立的索引域,這樣有個問題就是會導致倒排表的字典規模會比較大,特別是欄位屬性很多時。所有還有一種結構表示方法,如下:
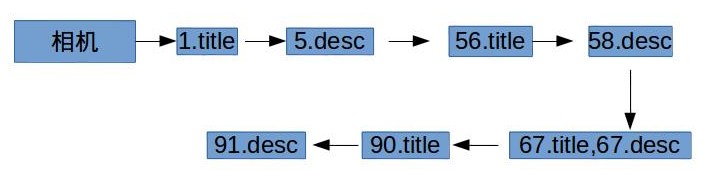
好處顯而易見,字典規模不會隨著屬性欄位增長而成倍增長,這在很多場景很有用的,比如字典放在記憶體中。還有一個優勢,方便域加權計算(weightd zone scoring)排序。
域加權評分
域加權評分公式:\(\sum_{i=1}^{l}g_is_i\) ,其中 \(g_i\) 為權重,值在[0-1]之間,且滿足\(\sum_{i=1}^{l}g_i=1\),\(s_i\)為查詢和文件的匹配情況,如為0表示不匹配,1為匹配。當然這個計算公司可以隨便定義,不只是限定要布林函式計算。現在問題產生了,即我們怎樣確定\(g_1,g_2,g_3\dots,g_l\)的值呢?這就引入機器學習的東西了,給定一定數量的樣本,先人工判斷預先設定一個固定的結果值,然後不斷調整變數g,計算出不同的結果並和預期設定的結果相比,誤差最小的值就是我們想要的。至於根據樣本計算求值的過程,需要了解數學中的規劃求解知識。
頻率及權重計算
到現在為止,基本上所有根據詞項搜尋出滿足要求文件集,它們都沒有優先順序的概念。而現實的需求不只是這樣,想像下這個場景,在一個數碼產品電商系統中,如果輸入“蘋果”,這樣會把所有包含有“蘋果”的商品都會搜尋出來。但是我們更希望那些出現“蘋果”次數多的商品排在更前面,原理很簡單,出現的次數越多,說明相關性更高。詞項t在文件d中出現的次數稱為詞項頻率(term frequency),記為 \(tf_{t,d}\)。但是這裡要引入一個概念叫做:逆文件頻率。什麼叫逆文件頻率呢?先說下什麼叫做文件頻率。這裡還是以具體場景舉例,還是以上面的數碼電商系統為例,比如“蘋果”在1867個商品描述中出現過,則可以說“蘋果”的文件頻率是1867。而“手機”這個詞在5693個商品描述中出現過,所以說“手機”的文件頻率是5693。現在問題來了,如果使用者輸入“蘋果手機”這個短語搜尋,根據中文分詞後再處理,會把所有包含“蘋果”和“手機”關鍵詞的商品都會搜尋出來,而且“手機”關鍵字出現的次數肯定會比“蘋果”多(原因是在數碼電商手機分類中,基本每個商品描述都會有“手機”關鍵詞),如果單按前面說的“詞項頻率”來計權排序,很有可能會把一些商品中出現“手機”次數很多的商品排在前面,但是這類商品中又沒有包含“蘋果”,這是違背使用者的意願的。為什麼會出現這個問題呢?原因就是“手機”關鍵詞基本會在每個商品描述中出現,它的意義倒顯得不是很重要了。相反,“蘋果”雖然只在少數商品中出現,但是每一次的出現,都應該計算更多的權值,因為它更能代表使用者的搜尋意願。所以可以得出這個結論:一個詞出現在文件的數量越多,它的權重越低。我們用 \(df_t\) 來標記文件頻率。但是大家應該會發現,在實際場景中,“文件頻率”的值是會很多大的,特別是海量資料系統中,這對於計算權重是很不方便和浪費(因為權重的目的是:體現兩個值的相對大小,而單個值是沒有意義的),所以可以通過對數函式來大副縮小這個值。我們如下方式來表達“逆文件頻率”:
\begin{equation}
idf_t=\log\frac{N}{df_t}
\end{equation}
其中N是所有文件的數量。所以\(idf_t\)最大值不會超過\(\log{N}\)。現在我們計算一個詞項在某個文件中出現時的權重計算公式:\(tf-idf_t=tf_d*idf_t\)。這個綜合公式即考慮到了詞項頻率,也考慮了逆文件頻率。
向量空間模型
我們在網路上看部落格或者新聞時,經常在旁邊給出一些與此文章相似的文章推薦,計算兩個文件的相似度經常要用到向量空間模型來計算。文件是由有限的詞項組成的,我們說兩篇文件看起來一樣,從第一感受上來說就是它們基本上包含了相同的詞項,並且各個詞項出現的頻率差不多。所以每們把每一篇文件看成一個向量值,各個分量值由組成文件的各個詞項在文件中所佔的分量比例。這樣,兩篇文件的相似度就轉化成了兩個向量值的夾角大小。正如下圖,在2維平面空間上,兩個向量的差距就是看它們的夾角大小:
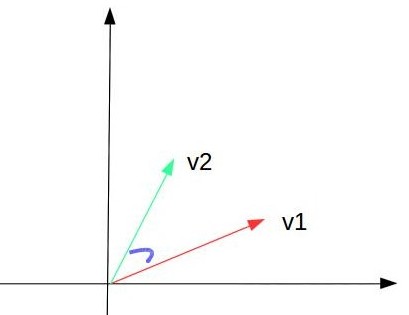
我們用向量的內積運算結果作為相似度值。為了使結果只關注本身的相似度值,做規一劃處理。每個向量通過向量長度做規一化處理後再計算內積。
\begin{equation}
sim(d_1,d_2)=\frac{\overrightarrow{V}(d_1).\overrightarrow{V}(d_2)}{|\overrightarrow{V}(d_1)||\overrightarrow{V}(d_1)|}
\end{equation}
我們根據一個查詢短語查詢相關聯的所有文件,並按相似度從大到小返回,可以按這樣的計算思路來:把查詢短語也看到一篇文件,分別和所有的文件進行相似度計算,按從大到小的值排序返回。
快速評分,排序
這裡用一段虛擬碼來描述下如何計算給定一個查詢q,計算並找出排在前M位的文件。下面我們簡化了查詢q中每個詞項的權重,存在的詞項都是相同的權重且設定為1,其實這是不影響總體排序的,因為排序是用相對比較而不是絕對值。
def calScore(q):
# 初始文件的評分為0,文件長度為N
scores = [0 for i in range(N)]
for t in q:
# 遍歷查詢q中所有的詞項
for d in post_list(t):
# 遍歷詞項t的倒排記錄表,累加詞項和文件的權重
scores[d] += wf_td
# 獲取權重最高的前M個資料
return top M of scores分析上面的演算法,很明顯的感覺就是,這樣的計算量太大了。如果查詢有m個詞項,這m個詞項的倒排表長度分別是\(l_1,l_2,l_3,\dots l_m\),則整個計算量是\(\sum_{i=1}^{m} l_i\)。特別是如果查詢詞項中某個或某幾個詞項的倒排表長度很長時,計算量顯得會很大。所以我們要用到一些技巧手法去優化下。
索引去除
最容易想到的優化點,就是我們可不可以考慮針對原始查詢做一些取捨,只關注查詢中那些idf值比較高的那些詞,即文件頻率高的那些詞。舉個例子,我們在3C電商搜尋中,根據“蘋果手機”檢索出排名最高的前20個商品。根據以往做法,根據分詞後的“蘋果”和“手機”兩個詞分別找到相應的倒排表,並依次掃描計算出最終的所有關聯的商品,並根據計算的權重值按從高到低排序,並取出前20個商品。但是細想下,針對3C商城來說,一個商品中包含“蘋果”已經足夠說明使用者的意願。而“手機”基本會出現在所有手機商品描述中,它的idf值是很低的,想當於那些“的,地,是”之類的停用詞。所以可以把這些idf值低的詞直接去掉,而這些詞的倒排表是很長的,所以可以節省很大部分的計算量。
勝者表(champion list)
上面的索引去除方法是從查詢進行優化裁剪。勝者表是從倒排表進行處理優化。我們針對每個查詢詞項,只取其倒排表中排名靠前的r個文件。這個r值的設定根據場景不同而異。而排名的依據可以用tf(詞項頻率)。
簇剪枝方法(cluster pruning)
顧名思義,這個方法就是把所有文件隨機(隨機是重點,要保證抽取的均勻分佈性)抽取\(\sqrt{N}\)(N是文件總數量)個出來,把它們分成\(\sqrt{N}\)堆,記為leader結點。然後把其它剩餘的文件分別劃到這\(\sqrt{N}\)堆中去。劃分的標準是該文件和哪堆的相似度最高就劃到哪裡,即分別計算出餘弦相似度比較最大的值。這樣當根據查詢短語檢索文件時,只要找出和這些事先分堆的\(\sqrt{N}\)個leader結點最相似的一個,然後分別和該leader結點所在的堆中的其它做計算比較。其實該演算法的重點是概率數學知識了。