本文主體內容譯於[DPDK社群文件],但並沒有逐字翻譯,在原文的基礎上進行了一些調整,增加了對TSS分類器的詳細闡述。
1. 概覽
本文描述了OVS+DPDK中的包分類器(datapath classifier -- aka dpcls)的設計與實現思路。本文的內容主要牽涉到分類器對封包流的分類及快取技術,並且對於一些典型場景下的細節給予解釋說明。
虛擬交換機與傳統硬體交換機的差別較大。硬體交換機通常都使用TCAM以求高效率的包分類與轉發。而虛擬交換機由於自身是純軟體實現,不能依靠特殊的硬體設計,為了達到較高的工作效率,在設計和實現上大量使用快取技術。OVS是一個相容OpenFlow協議的虛擬交換機軟體,發展比較迅速,基本上算是當前的業界網路虛擬化中的標杆與事實標準,OVS為了獲得較高的轉發效能,採用的基本思想也比較樸素:快取。
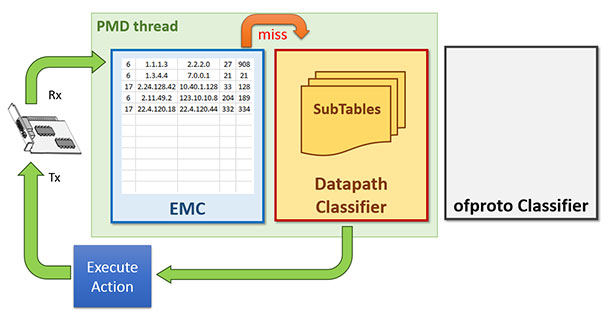
OVS的資料轉發面(datapath -- aka dp)有多種實現,其中比較著名的有基於Linux核心協議棧的實現與DPDK的實現。當採用DPDK的實現時,封包的處理流程將完全繞過核心協議棧。OVS+DPDK在封包的查詢匹配中,共有三級查詢表/快取的設計。最底一級是為完全精確匹配(Exact Match Cache -- aka EMC),如其名所示,這一級的查詢匹配無法實現範圍匹配、掩碼字首匹配等功能。中間一級就是本文的主角:dpcls,這一級的包分類器其實就是[這篇論文]描述的TSS分類器,使用論文中描述的TSS演算法,這一級的分類器可以實現範圍匹配、掩碼字首匹配等功能。如果單純的作為一個虛擬交換機,僅有最底一級與中間級已經足夠,而為了相容OpenFlow協議,OVS還有最上一級的查詢表:OpenFlow分類表(ofproto classifier table),其表項由OpenFlow控制器管理。下圖基本展示了這三級查詢表/快取的設計邏輯。
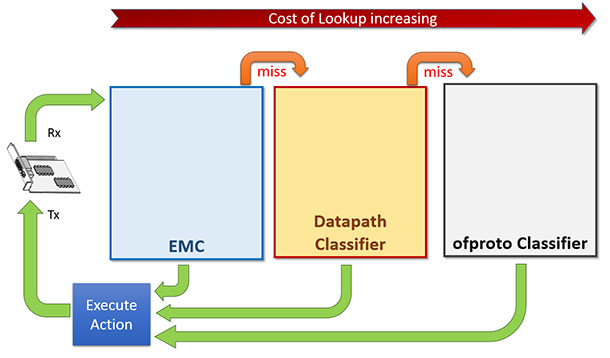
當一個包到達時,優先查詢最底一級的EMC表,命中則轉發,不命中則繼續查詢中間一級的包分類器,再不命中的話鍋就扔給OpenFlow的分類器了,再不命中就要扔給OpenFlow控制器了,邏輯很清晰。
當封包流很穩定,流的數量EMC表也能hold住的時候,轉發的效能取決於EMC表的查詢匹配效率。這算是理想狀態,現實世界很殘酷,EMC表的容量有限,在封包流的數量達到一定規模的時候,決定轉發效率的瓶頸就變成了中間一級的dpcls。所以dpcls本身的處理效率對於OVS+DPDK來說是很重要的一個關隘,其設計與實現是比較精巧的。
2. TSS分類演算法簡述
2.1. rule的定義
這裡簡單的介紹一下TSS分類器所使用的分類演算法,不牽涉任何優化手段,僅介紹原演算法本身。
定義rule就是單條的包過濾規則+動作,它可能長這樣:
1 Rule #1: ip_src=10.10.2.0/24 ip_dst=* protocol=UDP port_src=* port_dst=4789 actions=drop 2 Rule #2: ip_src=10.11.0.0/16 ip_dst=* protocol=TCP port_src=* port_dst=23 actions=output:3
為了描述清晰起見,rule中的過濾規則使用了穩定的五個欄位,即經典的五元組,但實際上rule可以使用任意多的欄位
rule中的過濾規則,或者叫匹配規則,是由多個單欄位過濾規則組成的,這些過濾規則符合,或者能轉化為以下的形式:
1 欄位值/掩碼字首
比如,對於IP地址來說,經常就是如下的形式
1 ip_src=192.168.0.0/16 2 ip_dst=33.23.12.0/24
對於IP頭中的協議欄位來講,由於協議欄位僅佔八位,多數情況下都是嚴格匹配,比如上面列出的兩個rule,其協議欄位都是嚴格匹配為UDP或TCP,故它們可以寫成如下形式
1 protocol=6/8(TCP) 2 protoco=17/8(UDP)
對於四層頭中的埠號,一般情況下在各種防火牆也好,OpenFlow流表也好,匹配規則一般都寫成精確匹配或者取值範圍的形式,精確匹配可以很簡單的寫成欄位值/字首掩碼的形式,無非就是掩碼是16位掩碼,而取值範圍要轉化為欄位值/字首掩碼的形式,就需要一定的轉化。我們舉個例子好了,取值範圍[12345, 33123]可以轉化為如下形式:
1 0011 0000 0011 1001 | 12345 2 0011 0000 0011 101* | 12346~12347 3 0011 0000 0011 11** | 12348~12351 4 0011 0000 01** **** | 12352~12415 5 0011 0000 1*** **** | 12416~12543 6 0011 0001 **** **** | 12544~12799 7 0011 001* **** **** | 12800~13311 8 0011 01** **** **** | 13312~14335 9 0011 1*** **** **** | 14336~16383 10 01** **** **** **** | 16384~32767 11 1000 0000 **** **** | 32768~33023 12 1000 0001 00** **** | 33024~33087 13 1000 0001 010* **** | 33088~33119 14 1000 0001 0110 00** | 33120~33123 15 1000 0001 0110 0011 | 33123
上面這個例子可能過分了一點,但足以說明一個問題:取值範圍在數學上是可以被轉化為欄位值/字首掩碼這種形式的。
至此,rule中的常見的三種過濾規則都可以轉化為欄位值/字首掩碼的形式
1 精確匹配 == 值/全bit掩碼 2 掩碼匹配 == 值/掩碼 3 取值範圍 == 可以轉化為多個 值/掩碼 的組合 4 任意值 == 掩碼位為0
將$欄位值$記為field,將字首掩碼記為mask,則單個匹配規則的記法如下:
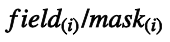
則一個rule的定義與記法就如下:
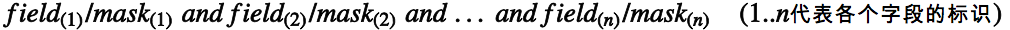
注意組成單條rule的多個匹配規則之間的邏輯關係是與/且,所以當匹配規則中有取值範圍時,一個rule要按上面的記法,就得拆分成多個rule
2.2. tuple的定義
按照上方的定義,我們可以寫出幾個rule,如下所示:
1 Rule #1: ip_src=192.168.0.0/16 2 Rule #2: ip_dst=23.23.233.0/24 protocol=6/8(TCP) port_dst=23/16 3 Rule #3: ip_dst=11.11.233.0/24 protocol=17/8(UDP) port_dst=4789/16 4 Rule #4: ip_src=10.10.0.0/16
在上面的例子中,我們省略了不關心的欄位。
以上面的4個rule中,我們認為Rule #1與Rule #4屬於同一個tuple,而Rule #2與Rule #3屬於同一個tuple。
即屬於同一個tuple中的所有rule有以下特點
1 使用相同的匹配欄位 2 每個匹配欄位都使用相同的掩碼長度
假如我們將匹配欄位僅限於傳統的五元組,並且把不關心的欄位也寫出來,如下面這樣:
1 Rule #1: ip_src=192.168.0.0/16 ip_dst=0/0 protocol=0/0 port_src=0/0 port_dst=0/0 2 Rule #2: ip_src=0/0 ip_dst=23.23.233.0/24 protocol=6/8(TCP) port_src=0/0 port_dst=23/16 3 Rule #3: ip_src=0/0 ip_dst=11.11.233.0/24 protocol=17/8(UDP) port_dst=0/0 port_dst=4789/16 4 Rule #4: ip_src=10.10.0.0/16 ip_dst=0/0 protocol=0/0 port_src=0/0 port_dst=0/0
可以明顯看出,其實屬於同一個tuple中的所有rule僅有一個特點:
1 匹配欄位的掩碼長度相同
即tuple的定義與記法如下:
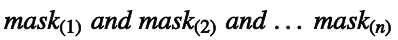
2.3. 分類演算法
分類演算法要解決的問題,可以描述如下
1 有一大堆rule 2 收到一個包 3 找到與這個包最匹配的rule,如果有多個匹配,按一定策略找出最優的那個
我們將最後一步的這個動作稱為match,即是匹配查詢
這不是一人困難的問題,至少在演算法角度來講,要解決這個問題並不困難,困難的是怎樣快速的解決這個問題。最樸素的做法是:用線性表把所有rule都串起來,每次match都是一次遍歷操作,時間複雜度O(N)
顯然樸素是不行的
2.4. TSS
TSS首先把所有的rule進行分類,分類的依據是同tuple的所有rule在一起。
其次對於同一個tuple下的所有rule,以雜湊表的形式將這些rule儲存起來。
依然用例子來說明,還是上方提到的四條rule,如下:
1 Rule #1: ip_src=192.168.0.0/16 ip_dst=0/0 protocol=0/0 port_src=0/0 port_dst=0/0 2 Rule #2: ip_src=0/0 ip_dst=23.23.233.0/24 protocol=6/8(TCP) port_src=0/0 port_dst=23/16 3 Rule #3: ip_src=0/0 ip_dst=11.11.233.0/24 protocol=17/8(UDP) port_src=0/0 port_dst=4789/16 4 Rule #4: ip_src=10.10.0.0/16 ip_dst=0/0 protocol=0/0 port_src=0/0 port_dst=0/0
它們將被分別兩個tuple,我們分別記為tuple #1與tuple #2,這兩個tuple的定義如下
1 Tuple #1: ip_src_mask=16 ip_dst_mask=0 protocol_mask=0 port_src_mask=0 port_dst_mask=0 2 Tuple #2: ip_src_mask=0 ip_dst_mask=24 protocol_mask=8 port_src_mask=0 port_dst_mask=16
每個tuple下都建一個雜湊表,我們分別記為ht #1與ht #2。tuple下的rule就儲存在相應的雜湊表中,如下所示
HT #1: Rule #1 | Rule #4 HT #2: Rule #2 | Rule #3
上面只講了雜湊表中的value是一個個的rule,但沒有說key是什麼,下面以Tuple #2中的Rule #2為例說明一下:
首先用tuple的掩碼去**與**rule中的各個**欄位值**,丟棄tuple不關心的位,得到:
1 ip_src=_ ip_dst=23.23.233 protocol=6 port_src=_ port_dst=23
然後把這些位拼接起來,就是雜湊表的key,在本例中,轉換為二進位制如下:
1 key = 0001 0111(23) 0001 0111(23) 1110 1001(233) 0000 0110(6) 0000 0000 0001 0111(23)
最後,用這個key去做雜湊,即是雜湊表的索引
2.5. 匹配過程
現在所有的rule都被分成了多個tuple,並儲存在相應tuple下的雜湊表中
當要對一個包進行匹配時,將遍歷這多個tuple下的雜湊表,一個一個查過去,查出所有匹配成功的結果,然後按一定策略在匹配結果中選出最優的一個。
依然是舉例說明,假設我們收到下面這樣一個包:
1 Packet #1: ip_src=192.168.1.2 ip_dst=23.23.233.234 protocol=UDP port_src=4344 port_dst=4789
首先在第一個tuple中進行匹配查詢
1) 將包的各個欄位與tuple定義的mask進行**與**操作,得到
1 ip_src=192.168 ip_dst=_ protocol=_ port_src=_ port_dst=_
2) 將有效位拼接起來,得到key
1 key = 1100 0000(192) 1010 1000(168)
並且這個key去Tuple #1下的雜湊表做查詢,則會命中Rule #1
3) 匹配成功,結果為Rule #1
然後在第二個tuple中進行匹配查詢,顯然也會匹配成功,命中Rule #3
最終,假設我們採用最長匹配策略的話,最終的匹配結果應當是Rule #3,因為該rule所屬於的tuple掩碼位數比Rule #1多。
2.6. TSS vs. 決策樹
決策樹又稱分類樹,是一種十分常用的分類、查詢、搜尋手段。但在網路封包的分類工作中,它並不適合,理由如下:
* 決策樹的插入與刪除效率不高。虛擬網路環境中的包分類器中的分類規則並不穩定,對於OVS+DPDK來講,將其視為OpenFlow交換機來使用的話,很多場景下都會導致中間一層的包分類器中的規則發生大量的插入與刪除操作。
* TSS的時間與空間複雜度均為O(N)。在最壞情況下,每個tuple中的雜湊表僅有一個條目,雜湊表的數目將等同於rules的數目,查詢效率將趨近於線性查詢。這不算糟糕,比起決策樹來說,還好上不少。
* TSS中可以使用任意數目的封包欄位進行匹配,而決策樹一旦成型,要增加或減少一個欄位就比較麻煩。在所有的匹配規則都是以傳統五元組(ip_dst+ip_src+protocol+port_dst+port_src)進行匹配的情況下,新插入一個使用了第六個欄位的匹配規則,這種事情對於TSS分類器來說,沒有任何額外的負擔,但對於決策樹來說,就需要調整整顆樹。
在TSS分類器中,查詢就意味著一個個的去查各個tuple下的雜湊表,直至某個雜湊表命中。所有雜湊表中的表項都是不重複、不互相覆蓋的,這個前置要求解決了TSS演算法中的一個蛋疼點:有多個匹配結果時如何最長匹配,在這個前置要求的前提下,一旦查詢命中,那麼只可能是唯一命中。分類器中的多個雜湊表的順序是隨機的,表和表項都是在工作的過程中動態建立的。
2.7. 小結
TSS分類演算法的時間複雜度為O(M),其中M是tuple的數量,空間複雜度是O(N),其中N是共計的rule的數量,無論是時間複雜度還是空間複雜度都在一個比較好的範圍裡。並且相較於其它分類演算法,對待rule的插入與刪除更友好
TSS分類演算法充分利用了網路封包欄位值的一些統計學特性,比如以掩碼字首為過濾規則的rule在實際防火牆或者路由器中是十分常見的。
Open vSwitch的資料轉發面在包分類上採用了該演算法,OVS+kernel datapath中的包分類在細節上與DPDK datapath有比較大的出入,並且隨著版本的更迭也在做一些調整,但兩者其實都使用的是TSS演算法,兩者細節處的不同也僅限於如何優化演算法的執行效率。關於OVS的總體設計決策,可以參見[這篇論文],論文沒有提及任何實現細節,僅在巨集觀上闡述了OVS的設計決策。
kernel datapath在歷代版本中嘗試過為tuple/雜湊表增加ranking權重、快取skb_hash與tuple/雜湊表等手段,以期望減少遍歷多個tuple/雜湊表時能儘快命中正確的tuple/雜湊表。
DPDK datapath優化的思路則是在TSS分類器下層建立一個小規格的、更快速的完全匹配EMC快取,以期望在大多數情況下不借助TSS分類器能正確轉發大部分流量。
TSS演算法,或者叫TSS分類器最初發表於[這篇論文],發表於1999年。
3. 對雜湊表進行排序以優化dpcls
在OVS 2.5 LTS分支上,每個PMD執行緒都會建立一個TSS分類器例項。每次查詢都是對分類器中雜湊表的遍歷,平均開銷為N/2,這裡的N指的是雜湊表的數量。儘管這樣理論上看起來很完美,但實際開銷中,算雜湊值也是一部分比較大的開銷:每查一個雜湊表,都要根據tuple的定義重新掩一次匹配欄位,重新算一次雜湊值。
為了一定程度上緩解這個問題,OVS在2.6版本中,為每個雜湊表都增加了一個ranking值,這個ranking值以雜湊表命中查詢的次數為準,這很好理解,將熱度高的雜湊表提到前面來,熱度低的雜湊表放在後面,以儘量減少平均查詢雜湊表的次數。
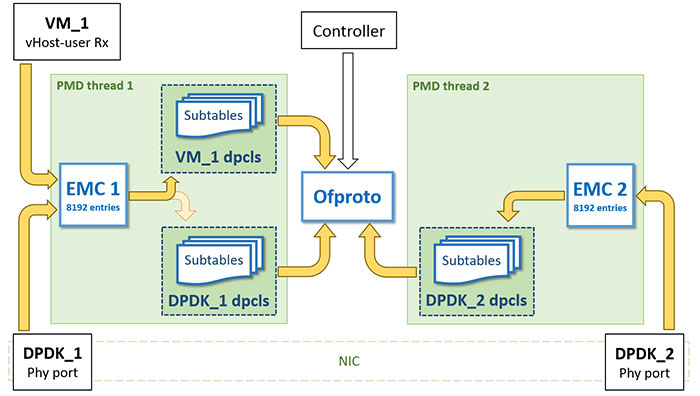
除了上面的改進,在2.6版本中,不再是為每個PMD執行緒建立一個dpcls例項,而是為每個ovs-port建立一個dpcls例項。這個改進就是工程實踐上的經驗性改進了,由於同一個port收上來的包有很強的相似性,這樣為每個port都建立一個dpcls例項,這樣dpcls例項中的雜湊表數量,即tuple的數量會變少,變相的也提高了查詢效率。
下圖展示了多個dpcls的邏輯:下圖中有三個ovs-port,其中有兩個ovs-port(DPDK_1與DPDK_2)背後是物理網路介面,另外一個ovs-port(VM_1)背後是vHost User型的虛擬port。每個dpcls例項將負責從對應ovs-port收上來的包的分類工作。比如,比VM_1介面收上來的包由執行緒PMD thread 1處理,該執行緒先進EMC對包進行匹配,匹配失敗後該執行緒負責對包進行掩碼處理,算雜湊值,然後以該雜湊值去VM_1 dpcls中去查詢。
4. 模糊匹配(wildcard matching)的實現技術
這裡闡述的是中間一級的TSS分類器如何使用雜湊表實現上層OpenFlow表項指導的模糊匹配功能。
假設OVS OpenFlow流表中增加了一條流表,其匹配規則如下所示:
1 Rule #1: Src IP = "21.2.10.*"
這個規則可以通過如下的ovs命令新增進流表中:
1 ovs-ofctl add-flow br0 dl_type=0x0800,nw_src=21.2.10.1/24,actions=output:2
當OVS收到一個源IP欄位值為21.2.10.5的包時,並假設EMC與dpcls都查詢失敗,這個包將送至ofproto classifier中進行匹配,並且會匹配至上面新增的這條規則。匹配成功之後,相應的學習機制會使得dpcls與EMC中都新增一個相應的表項。EMC中新增的表項是一個嚴格匹配表項,沒有模糊匹配功能,而dpcls中新增的表項將帶有模糊匹配,我們現在要闡述的就是dpcls如何新增這個表項。
下面的幾個小節將一步一步的闡述OVS+DPDK如何建立起tuple雜湊表,如何進行查詢。我們假設在進行下面幾個小節的操作之前,整個OVS+DPDK在中間層和下層,即dpcls與EMC這兩層,是不存在任何條目、表項的。
4.1. 單ovs-port場景
上文中說過,在OVS 2.6版本之後,實際實現中是為每一個ovs-port建立一個獨立的dpcls例項,下面的闡述中,將先介紹簡單的場景,先介紹在單ovs-port場景,僅有一個dpcls例項的情況下,包分類是如何進行的,之後在單ovs-port場景的基礎上再介紹實際實現中的多ovs-port場景,多dpcls例項下包分類是如何進行的
4.1.1新增第一個Rule
在向dpcls中的某個雜湊表新增Rule #1之前,我們先要建立一個Mask #1。這個Mask如下
1 Mask #1: 0xFF.FF.FF.00
Mask建立完成後,下一步就是找到該Rule應屬的雜湊表,或者建立一個新的雜湊表。
再接下來,為了將這個Rule新增進雜湊表中,就需要先計算這個Rule的雜湊值,流程如下圖所示:
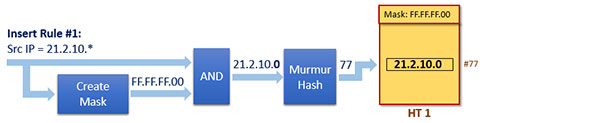
上圖將Rule #1新增進了名為HT 1的雜湊表中,除了Rule #1外,HT 1這張表中還會儲存很多與Rule #1相似的規則,而所謂相似,就是指它們位於同一個tuple中,換名話說,即是這些Rule對應的Mask都相同
即下面這個Rule也會被新增進HT 1中,所有同一個雜湊表中的Rule的Mask都是相同的
1 Rule #1A: Src IP="83.83.83.*"
4.1.2. 查詢匹配過程
現在有一個包被收上來,其源IP地址為21.2.10.99,我們稱這個包為Packet #1,假設現在OVS的dpcls中除了HT 1之外沒有其它的雜湊表,那麼這個包將在該表中進行匹配搜尋操作。
首先會將該包與Mask #1進行與操作,將與操作的操作結構進行雜湊運算,得到雜湊值,然後就查出結果了。如下圖所示
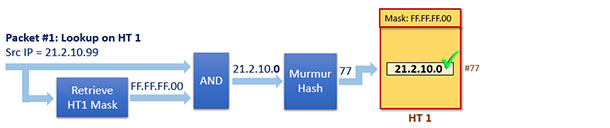
4.1.3. 新增第二個Rule
現在假設我們要新增第二個Rule,有了前面第一個Rule如何新增的闡述,這裡就不闡述的那麼詳細了。這次要新增的Rule依然是源IP地址匹配,但掩碼變成了16位:
1 Rule #2: Src IP = "7.2.*.*"
該Rule的對應的Mask是一個全新的Mask
1 Mask #2: 0xFF.FF.00.00
這是一個全新的Mask,意味著這個Rule屬於一個全新的tuple,一個新的雜湊表會被建立,之後該Rule會被插入到新的雜湊表中,我們記這個新的雜湊表為HT 2。整個插入過程如下圖所示:
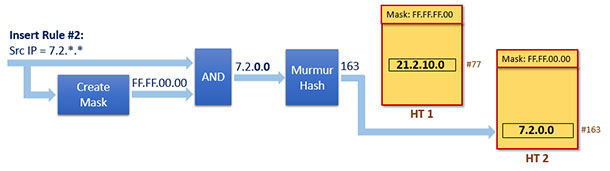
4.1.4. 第二次查詢匹配
現在收上來一個包,其源IP地址為7.2.45.67,我們記該包為Packet #2
現在dpcls中有兩個雜湊表,匹配查詢將試圖在這兩個表上都執行,直到成功匹配為止。我們假設HT 1是首個被執行搜尋的雜湊表,則顯然會查詢失敗,其查詢匹配過程如下:
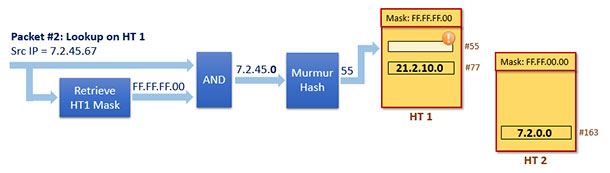
由於查詢匹配失敗,所以匹配流程將繼續在HT 2上執行,流和如下:
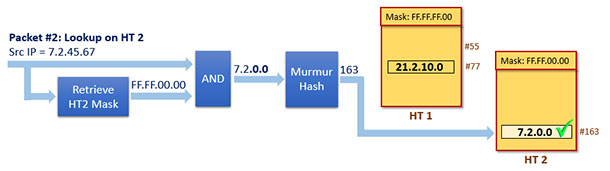
這一次匹配成功!
4.1.5. 小結
通過上面的圖例與闡述,重新溫習了TSS分類器的分類演算法,也認識了OVS+DPDK對於TSS分類器的實現。但故事依然沒有結束,在上面的例子中,整個OVS+DPDK的中間層僅有一個dpcls例項,所有OVS收到的包都由這個dpcls進行匹配查詢操作,這樣做是可行的,但與實際情況並不符合。前文說過,在2.6版本之後,OVS為每個ovs-port都建立了一個dpcls例項,下面我們將繼續分析在多port多dpcls例項的情景下,Rule是如何被插入的,包是如何被匹配的。
4.2. 多ovs-port場景
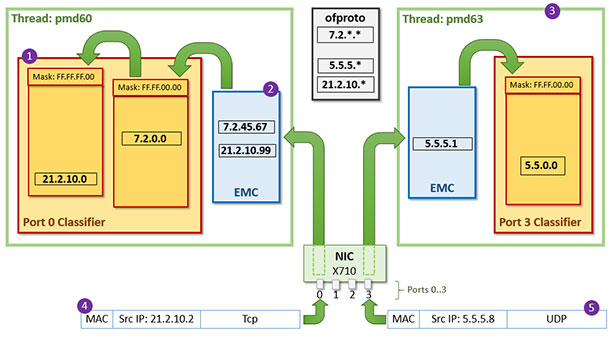
下圖展示了兩個PMD執行緒(PMD60與PMD63),兩個ovs-port(port0與port3),port0由pmd60負責收包,port3由pmd63負責收包,每個port都有自己的dpcls例項與EMC快取。這種場景下發生的故事:
1) 假設有兩個包到達了port0,其源IP地址分別是21.2.10.99與7.2.45.67,其假設上一章闡述的故事均發生在port0上
2) 即port0的dpcls中會有兩個tuple/雜湊表,且其EMC中分別儲存著源IP地址為21.2.10.99與7.2.45.67這兩個包的action
3) 有一個包到達了port3,其源IP地址為5.5.5.1,包收上來之後在port3下的dpcls中生成了一個5.5.0.0/16的rule
4) 現在繼續收包,port0上收到一個源IP地址為21.2.10.2的包,EMC中查無記錄,於是去dpcls中查詢,查詢過程如上一章所述,如果運氣不好的話需要查詢兩張雜湊表。查詢匹配成功後除了包將被轉發出去,也會在EMC中下該包的快取。
5) port3上收到一個源IP地址為5.5.5.8的包,EMC中查無記錄,上dpcls查詢,一次命中。包被轉發,同時下EMC快取