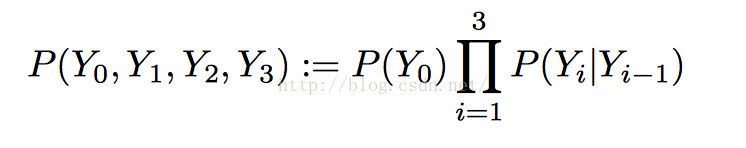Markov Model 馬可夫模型 & Hidden Markov Model 隱馬可夫模型
馬可夫模型是什麼?
是一種隨機模型,這種模型假設系統將來的狀態是由當前的狀態轉變而來的, 並且不受當前狀態之前的狀態影響。
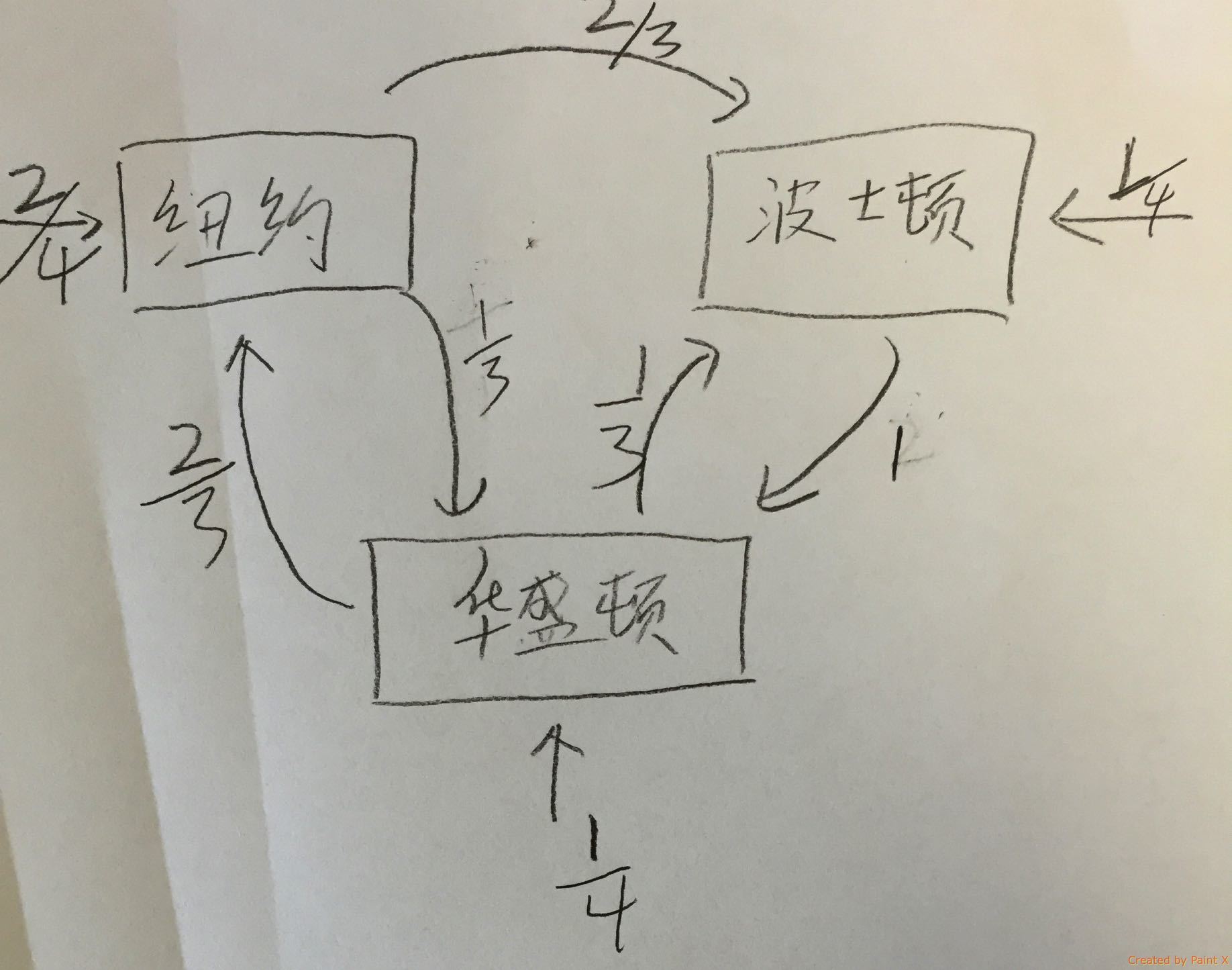
- 以城市旅遊為例子: 我先去紐約 然後去波士頓 最後去華盛頓, 那麼我們認為 到波士頓是基於紐約而來的,同理到華盛頓是基於 波士頓而來的。
馬可夫鏈是什麼?
就是系統狀態轉移的路徑。 從以下的例子可以得出 4條 序列, 那麼將這 4 條
- 以城市旅遊為例子: A 同學的路徑是從 紐約 -> 波士頓-> 華盛頓
B 同學的路徑是從 華盛頓 -> 紐約 -> 波士頓
C 同學的路徑是從 紐約 -> 華盛頓 -> 波士頓
D 同學的路徑是從 波士頓 -> 華盛頓 -> 紐約
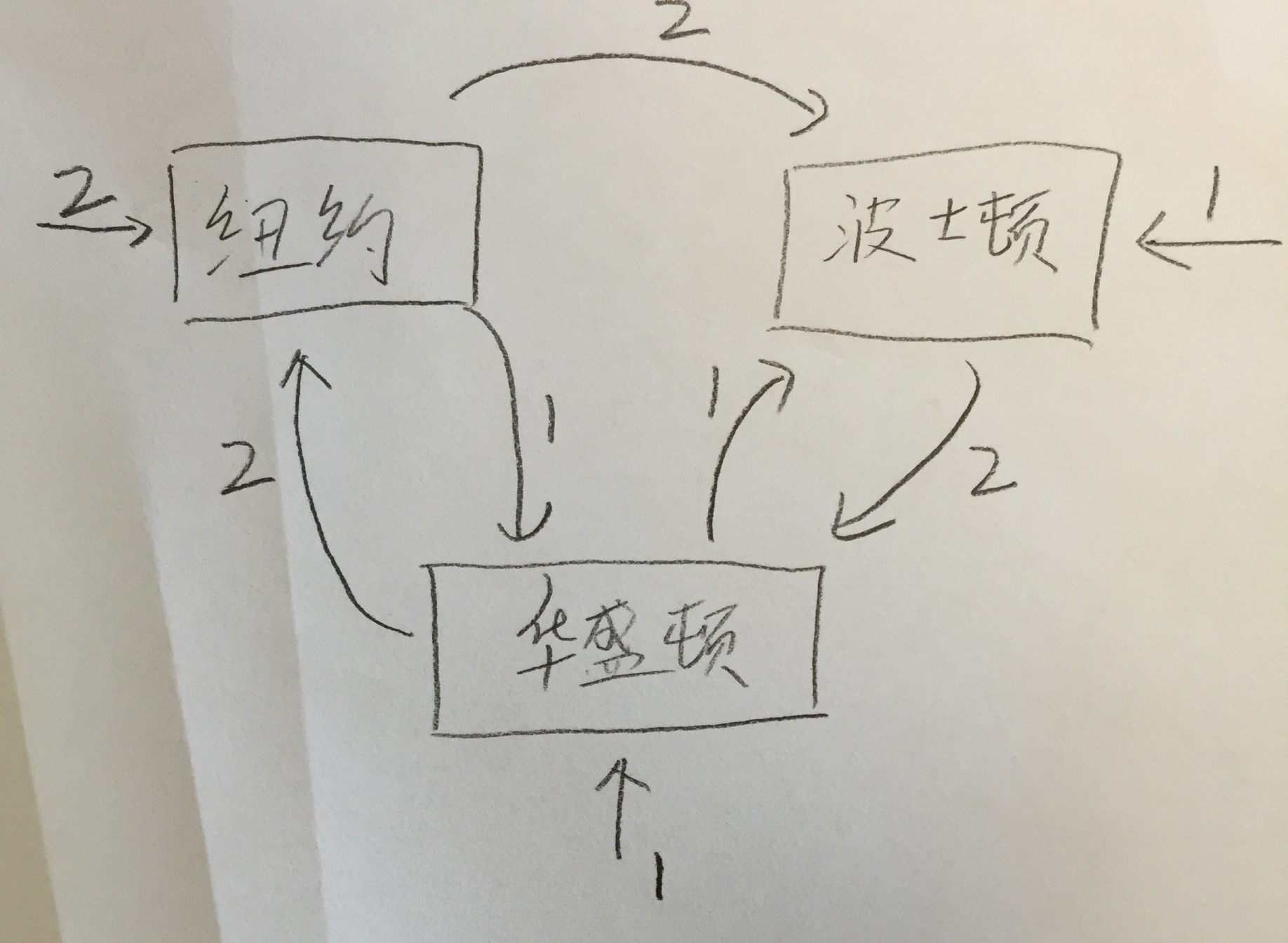
以上就是一個完整的markov chain, 從這個chain我們能得到什麼資訊呢?
首先 從紐約出發的下一個城市有兩種可能 1. 波士頓 2. 華盛頓 那麼從紐約出發到波士頓的概率就是 2/3. 到華盛頓的概率就是 1/3。
另外, 那我們能不能得到從哪個城市出發呢? 一共有四個人, 出發城市總數為4. 那麼從紐約出發的概率為 2/4 。
由此我們能得到以下
由此我們就很容易的可以預測 某個人的旅遊路線。為了更好的闡述該問題我們可以講問題轉化為一個maximization問題!
假設我需要去 四個城市旅遊,已知markov model, 那麼我們可以通過優化以下公式來找出最受歡迎的路線(即概率最大的路線)
定義 Y 屬於(0, 1, 2, 3) 為四個城市 / P(Y) 為出發城市的概率 / P(Yi | Yi-1) 是 以 Yi-1 為出發城市 到Yi 城市的概率
什麼是隱馬可夫模型, 它是在馬可夫模型上包含的一個隱形變數,但是這個隱形變數就是我們想要觀察的變數。換句話說就是, 我們不能直接觀察我們的目標變數,但是我們能觀 察到的是一個和目標變數有關的變數。
還是以城市旅遊為例子。
- 以城市旅遊為例子:(但是這次我們不僅僅知道旅遊的城市也知道了在城市的花費)
A 同學的路徑是從 紐約( $800) -> 波士頓($400)-> 華盛頓($600)
B 同學的路徑是從 華盛頓($550) -> 紐約($900) -> 波士頓($450)
C 同學的路徑是從 紐約($750) -> 華盛頓($650) -> 波士頓($325)
D 同學的路徑是從 波士頓($425) -> 華盛頓($600) -> 紐約($750)
根據 在各個城市的花費,我們能分別對各個城市花費找出相對應的 Normal Distribution
例如 紐約就是 N(800, 61)
通過以上資訊我們能得出一個 Hidden Markov Model 如下
當準備好 hidden markov model 能做什麼呢?
我們現在知道了一個人在旅途中的花費是這樣的. 875 (城市1)
紐約 N(800, 61) 波士頓 N(400, 47) 華盛頓 N(600, 35)
例如: 將 875 分別帶入三個城市的分佈中求出概率 發現 紐約的概率最大, 即該城市1為紐約
一次類推我們能找到所有的最優解。
例題
加入我們已知 在四個城市的花費 x1 = 355 / x2 = 339 / x3 = 148 / x4 = 50, 預測這四個城市各是什麼?
通過以上我們知道,就是找出這四個城市概率的最大值,轉化問題為一個maximization 問題。
定義 Y 屬於(0, 1, 2, 3) 為四個城市 / P(Y) 為出發城市的概率 / P(Yi | Yi-1) 是 以 Yi-1 為出發城市 到Yi 城市的概率
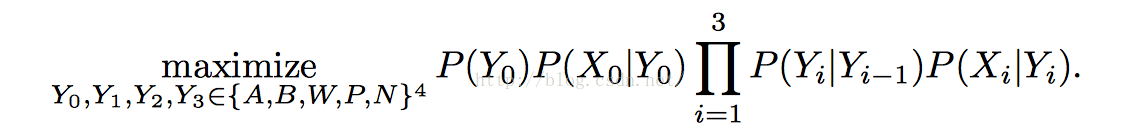
相關文章
- 10_隱馬爾可夫模型隱馬爾可夫模型
- 隱馬爾可夫模型詳解隱馬爾可夫模型
- ML-隱馬爾可夫模型隱馬爾可夫模型
- 隱馬爾可夫模型(HMM)詳解隱馬爾可夫模型HMM
- 隱馬爾可夫模型 | 賽爾筆記隱馬爾可夫模型筆記
- 機器學習之隱馬爾可夫模型機器學習隱馬爾可夫模型
- HMM隱馬爾可夫模型來龍去脈(二)HMM隱馬爾可夫模型
- NLP-隱馬爾可夫模型及使用例項隱馬爾可夫模型
- 用簡單易懂的例子解釋隱馬爾可夫模型隱馬爾可夫模型
- 域結構進化的馬爾可夫模型馬爾可夫模型
- CVPR 2021 | 時間序列疾病預測的因果隱馬爾可夫模型隱馬爾可夫模型
- 維特比演算法和隱馬爾可夫模型的解碼維特比演算法隱馬爾可夫模型
- 2022-05-17-馬爾科夫鏈之傳統馬爾可夫鏈馬爾科夫馬爾可夫
- [work] 一階 二階馬爾可夫馬爾可夫
- 理解馬爾可夫決策過程馬爾可夫
- 【機器學習】--隱含馬爾科夫模型從初識到應用機器學習馬爾科夫模型
- 「馬爾可夫決策過程」學習筆記馬爾可夫筆記
- 在 Swift 中使用馬爾可夫鏈生成文字Swift馬爾可夫
- 馬爾可夫鏈你知道多少?Python視覺化解析MCMC馬爾可夫Python視覺化
- [譯] 用 Python 實現馬爾可夫鏈的初級教程Python馬爾可夫
- AI產品經理必修:揭開演算法的面紗(隱含馬爾可夫)AI演算法馬爾可夫
- R資料分析:縱向分類結局的分析-馬爾可夫多型模型的理解與實操馬爾可夫多型模型
- 馬爾可夫鏈是個什麼鬼?圖文詳解告訴你!馬爾可夫
- 今天是霧霾,明天是什麼?馬爾可夫鏈告訴你馬爾可夫
- Markov Chain & Monte CarloAI
- 中文分詞的探索,CRF(條件隨機場)和HMM(隱馬爾可夫模型)用於分詞的對比,以及中文分詞的評估中文分詞CRF條件隨機場HMM隱馬爾可夫模型
- CDM(Conceptual Data Model,概念資料模型)和 PDM(Physical Data Model,物理資料模型)模型
- 一個馬爾科夫鏈例項馬爾科夫
- 盒子模型Box Model簡介模型
- DOM (文件物件模型(Document Object Model))物件模型Object
- 馬爾科夫鏈的穩態分佈馬爾科夫
- EF Core預編譯模型Compiled Model編譯模型Compile
- ASP.NET Core MVC 之模型(Model)ASP.NETMVC模型
- 儲存載入模型model.save()模型
- Attention Model(注意力模型)思想初探模型
- 馬爾科夫鏈隨機文字生成器馬爾科夫隨機
- 強化學習組隊學習task02——馬爾可夫決策過程及表格型方法強化學習馬爾可夫
- LLM大模型: Segment Anything Model原理詳解大模型
- 業務領先模型(Business Leadership Model; BLM)模型