什麼是快速排序

快速排序簡介

快速排序（英文名：Quicksort，有時候也叫做劃分交換排序）是一個高效的排序演算法，由Tony Hoare在1959年發明（1961年公佈）。當情況良好時，它可以比主要競爭對手的歸併排序和堆排序快上大約兩三倍。這是一個分治演算法，而且它就在原地排序。

所謂原地排序，就是指在原來的資料區域內進行重排，就像插入排序一般。而歸併排序就不一樣，它需要額外的空間來進行歸併排序操作。為了線上性時間與空間內歸併，它不能線上性時間內實現就地排序，原地排序對它來說並不足夠。而快速排序的優點就在於它是原地的，也就是說，它很節省記憶體。

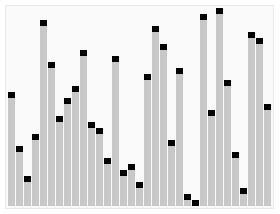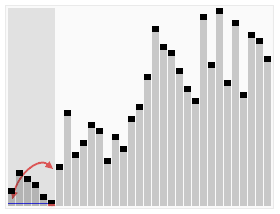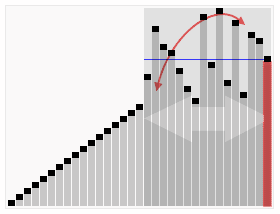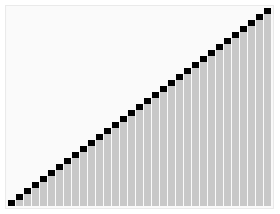
引用一張來自維基百科的能夠非常清晰表示快速排序的示意圖如下：

快速排序的分治思想

由於快速排序採用了分治演算法，所以：

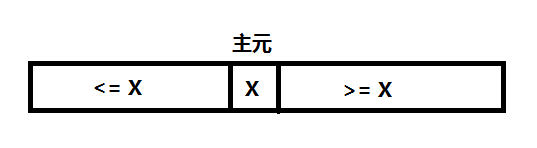
一、分解：本質上快速排序把資料劃分成幾份，所以快速排序通過選取一個關鍵資料，再根據它的大小，把原陣列分成兩個子陣列：第一個陣列裡的數都比這個主後設資料小或等於，而另一個陣列裡的數都比這個主後設資料要大或等於。

二、解決：用遞迴來處理兩個子陣列的排序。 （也就是說，遞迴地求上面圖示中左半部分，以及遞迴地求上面圖示中右半部分。）

三、合併：因為子陣列都是原址排序，所以不需要合併操作，通過上面兩步後陣列已經排好序了。

所以快速排序的主要思想是遞迴與劃分。

如何劃分

當然最重要的是它的複雜度是線性的，也就是Θ(n)$\mathrm{\Theta }(n)$

個劃分的子程式。

Partition(A,p,q)   // A[p,..q] 
1   x=A[p]   // pivot=A[p] 主元 
2   r=p 
3   for i=p+1 to q
4       do if A[i]<=x
5          then r=r+1 
6             exch A[r]<->A[i] 
7   exch A[p]<->A[r] 
8   return r // i pivot 

這就是劃分的虛擬碼，基本的結構就是一個for迴圈語句，中間加上了一個if條件語句，它實現了對子陣列A[p...q]$A[p...q]$

的原址排序。

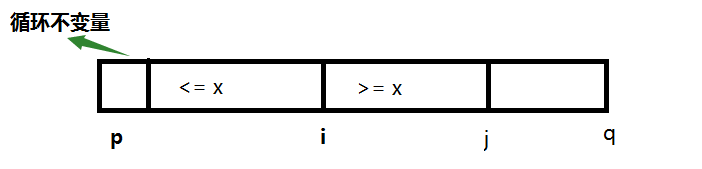
剛開始時i$i$

等於p$p$，j$j$等於p+1$p+1$。在這個迴圈中查詢i下標的資料，如果它比x$x$大，那就將其存放到“>=x”區域並將j$j$加1後進行下一次迴圈。而如果它比x$x$小，那就要做些動作來維持迴圈不變數了。將i$i$的下標加1後將下標i對應的資料和下標j所對應的資料互換位置。然後再移動區域的界限並開始下一次迴圈。

那麼這個演算法在n個資料下的執行時間大約是O(n)$O(n)$

，因為它幾乎把每個數都比較了一遍，而每個步驟所需的時間都為O(1)$O(1)$。

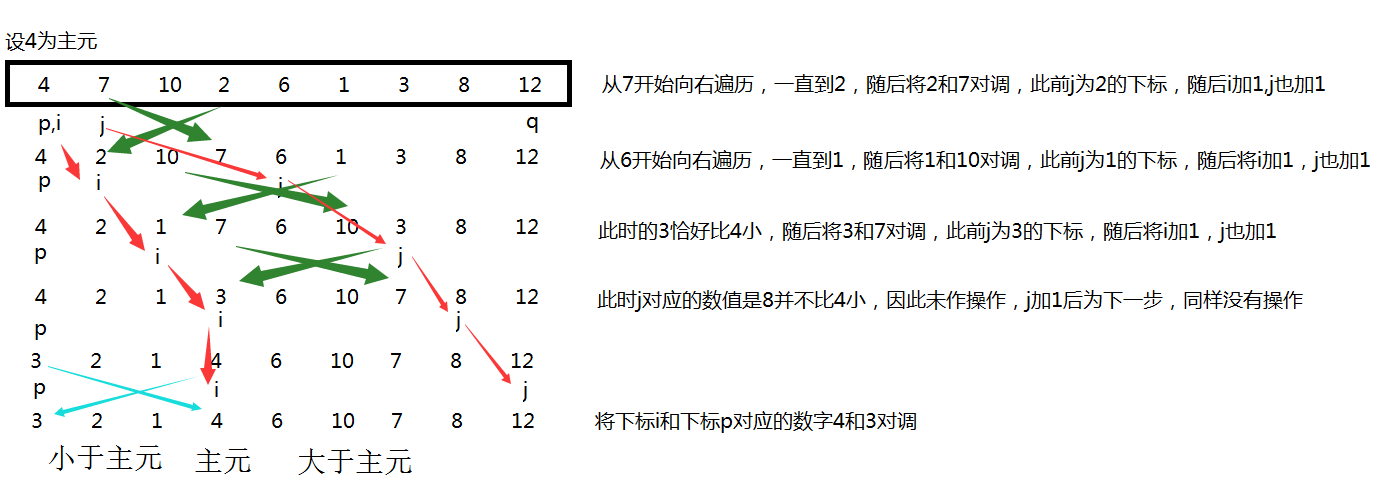
（倒數第二行的3和4的位置錯了，應該是到最後一行的時候才交換過來）

上面這幅圖詳細的描述了Partition過程，每一行後也加了註釋。

將遞迴的思想作用於劃分上

有了上面這些準備工作，再加上分治的思想實現快速排序的虛擬碼也是很簡單的。

Quicksort(A,p,q) 
1   if p<q 
2     then r=Partition(A,p,q)   
3          Quicksort(A,p,r-1) 
4          Quicksort(A,r+1,q) 

為了排序一個陣列A的全部元素，初始呼叫時Quicksort(A,1,A.length)$Quicksort(A,1,A.length)$

。

實現示例

// Java
package com.nomasp;

/**
 * Created by nomasp on 16/9/24.
 */
public class QuickSort {

    private int[] array;

    public QuickSort(int[] array) {
        this.array = array;
    }

    private void swap(int x, int y) {
        int tmp = array[x];
        array[x] = array[y];
        array[y] = tmp;
    }

    private int partition(int start, int end) {
        int pivot = array[start];
        int r = start;
        for (int i = start + 1; i <= end; i++) {
            if (array[i] <= pivot) {
                r += 1;
                swap(r, i);
            }
        }
        swap(start, r);
        return r;
    }

    private void quickSort(int start, int end) {
        if (start < end) {
            int r = partition(start, end);
            quickSort(start, r - 1);
            quickSort(r + 1, end);
        }
    }

    public int[] sort() {
        quickSort(0, array.length - 1);
        return array;
    }

    public int[] sort(int start, int end) {
        quickSort(start, end);
        return array;
    }
}

快速排序的演算法分析

相信通過前面的諸多實踐，大家也發現了快速排序的執行時間依賴於Partition過程，也就是依賴於劃分是否平衡，而歸根結底這還是由於輸入的元素決定的。

如果劃分是平衡的，那麼快速排序演算法效能就和歸併排序一樣。

如果劃分是不平衡的，那麼快速排序的效能就接近於插入排序。

怎樣是最壞的劃分

1）輸入的元素已經排序或逆向排序
2）每個劃分的一邊都沒有元素

也就是說當劃分產生的兩個子問題分別包含了n-1個元素和0個元素時，快速排序的最壞情況就發生了。

T(n)=T(0)+T(n−1)+$T(n)=T(0)+T(n-1)+$

\Theta(n)=Θ(1)+T(n−1)+Θ(n)=Θ(n−1)+Θ(n)=Θ(n2)$=\mathrm{\Theta }(1)+T(n-1)+\mathrm{\Theta }(n)=\mathrm{\Theta }(n-1)+\mathrm{\Theta }(n)=\mathrm{\Theta }(n^2)$

這是一個等差級數，就和插入排序一樣。它並不比插入排序快，因為當同樣是輸入元素已經逆向排好序時，插入演算法的執行時間為Θ(n)$\mathrm{\Theta }(n)$

。但快速排序仍舊是一個優秀的演算法，這是因為在平均情況下它已經很高效。

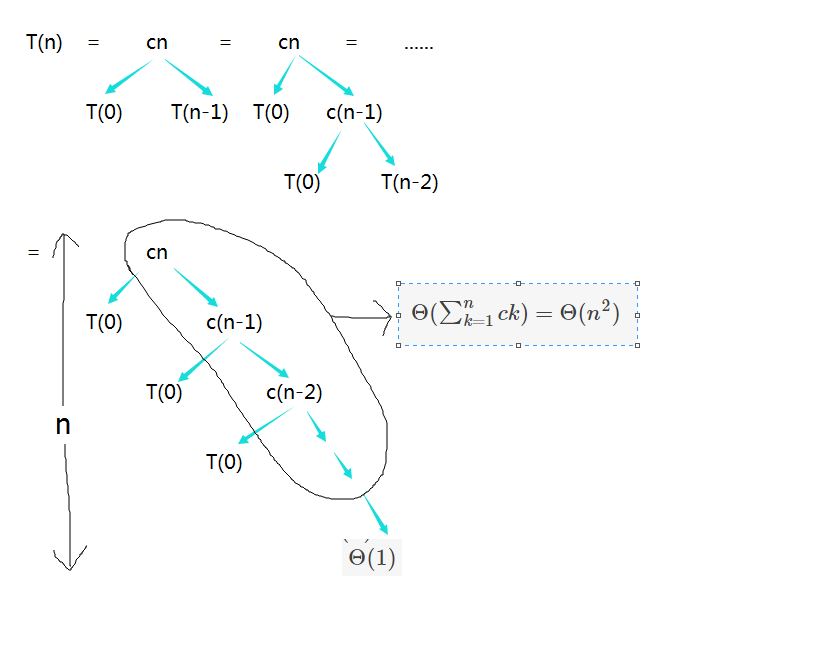
我們為最壞情況畫一個遞迴樹。

這是一課高度不平衡的遞迴樹，圖中左邊的那些T(0)$T(0)$

的執行時間都為Θ(1)$\mathrm{\Theta }(1)$，而總共有n個。

所以演算法的中執行時間為：

T(n)=Θ(n)+Θ(n2)=Θ(n2)$T(n)=\mathrm{\Theta }(n)+\mathrm{\Theta }(n^2)=\mathrm{\Theta }(n^2)$

最壞劃分的演算法分析

通過上面的圖示我們知道了在最壞情況下快速排序的複雜度是Θ(n2)$\mathrm{\Theta }(n^2)$

，但以圖示的方式並不是一種嚴謹的證明方式，我們應該使用代入法來證明它。

當輸入規模為n時，時間T(n)$T(n)$

有如下遞迴式：

T(n)=max⏟0≤r≤n−1(T(r)+T(n−r−1))+Θ(n)$T(n)=\underset{0\le r\le n-1}{\underbrace{max}}(T(r)+T(n-r-1))+\mathrm{\Theta }(n)$

除去主元后，在Partition函式中生成的兩個子問題的規模的和為n-1，所以r的規模才是0到n-1。

假設T(n)≤cn2$T(n)\le c{n}^2$

成立，其中c為常數這個大家都知道的。於是上面的遞迴式為：

T(n)≤max⏟0≤r≤n−1(cr2+c(n−r−1)2)+Θ(n)≤c∗max⏟0≤r≤n−1(r2+(n−r−1)2)+Θ(n)$T(n)\le \underset{0\le r\le n-1}{\underbrace{max}}(c{r}^2+c(n-r-1{)}^2)+\mathrm{\Theta }(n)\le c\ast \underset{0\le r\le n-1}{\underbrace{max}}(r^2+(n-r-1{)}^2)+\mathrm{\Theta }(n)$

1）而r2+(n−r−1)2$r^2+(n-r-1{)}^2$

對於r的二階導數為正，所以在區間0≤r≤n−1$0\le r\le n-1$的右端點取得最大值。

於是有max⏟0≤r≤n−1(r2+(n−r−1)2)≤(n−1)2=n2−2n+1$\underset{0\le r\le n-1}{\underbrace{max}}(r^2+(n-r-1{)}^2)\le (n-1{)}^2=n^2-2n+1$

，所以對於T(n)$T(n)$有：

T(n)≤cn2−c(2n−1)+Θ(n)$T(n)\le c{n}^2-c(2n-1)+\mathrm{\Theta }(n)$

最終因為我們可以選擇一個足夠大的c$c$

，來使得c(2n−1)$c(2n-1)$大於Θ(n)$\mathrm{\Theta }(n)$，所以有T(n)=O(n2)$T(n)=O(n^2)$。

2）r2+(n−r−1)2$r^2+(n-r-1{)}^2$

對於r的二階導數為正，所以在區間0≤r≤n−1$0\le r\le n-1$的左端點取得最小值。

於是有max⏟0≤r≤n−1(r2+(n−r−1)2)≥(n−1)2=n2−2n+1$\underset{0\le r\le n-1}{\underbrace{max}}(r^2+(n-r-1{)}^2)\ge (n-1{)}^2=n^2-2n+1$

，所以對於T(n)$T(n)$有：

T(n)≥cn2−c(2n−1)+Θ(n)$T(n)\ge c{n}^2-c(2n-1)+\mathrm{\Theta }(n)$

同樣我們也可以選擇一個足夠小的c$c$

，來使得c(2n−1)$c(2n-1)$小於Θ(n)$\mathrm{\Theta }(n)$，所以有T(n)=Ω(n2)$T(n)=\mathrm{\Omega }(n^2)$。

綜上這兩點得到T(n)=Θ(n2)$T(n)=\mathrm{\Theta }(n^2)$

怎樣是最好的劃分

當Partition將陣列分為n/2$n/2$

和n/2$n/2$兩個部分時是最高效的。此時有：

T(n)=2T(n/2)+Θ(n)=Θ(nlgn)$T(n)=2T(n/2)+\mathrm{\Theta }(n)=\mathrm{\Theta }(nlgn)$

怎樣是平衡的劃分

快速排序的平均執行時間更接近於其最好情況，而非最壞情況。

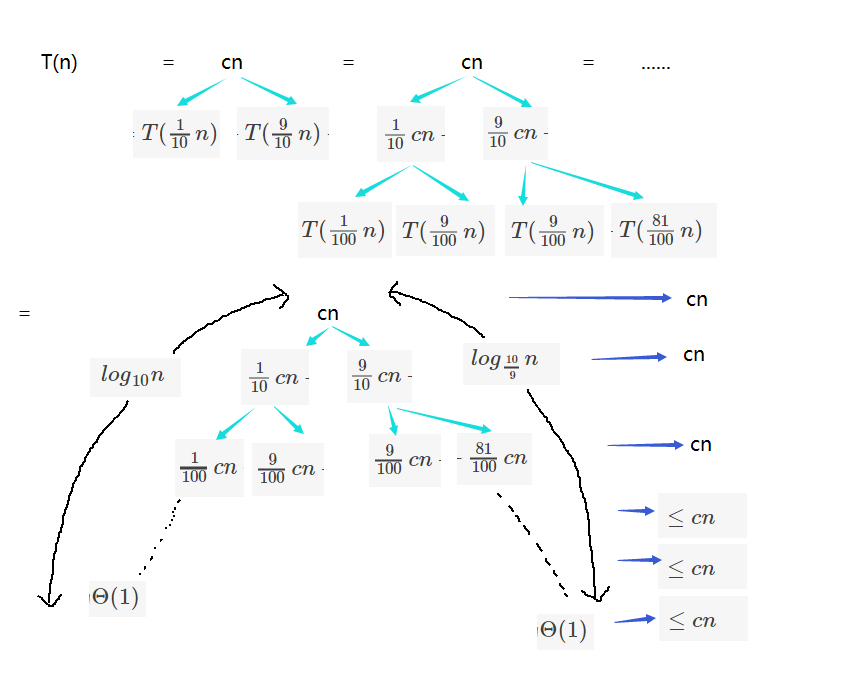
此處有一個經典的示例，將陣列按1：9$1：9$

的比例進行劃分會怎樣呢？這種劃分看似很不平衡，但真的會因此而影響效率麼？

其中此時的遞迴式是：

T(n)=T(110n)+T(910n)+Θ(n)$T(n)=T(\frac{1}{10}n)+T(\frac{9}{10}n)+\mathrm{\Theta }(n)$

這裡依舊通過遞迴樹來觀察一番。

因為每次都減少十分之一，需要減多少次才能達到n呢，也恰好也是以10為底對數的定義。所以左側的高度為log10n$lo{g}_{10}n$

了，相應的右側的高度為log109n$lo{g}_{\frac{10}{9}}n$。

所有那些葉子加在一起也只有Θ(n)$\mathrm{\Theta }(n)$

，所以有：

T(n)≤cn∗log109n+Θ(n)$T(n)\le cn\ast lo{g}_{\frac{10}{9}}n+\mathrm{\Theta }(n)$

其實T(n)$T(n)$

的下界也漸近為nlgn$nlgn$，所以總時間為：

T(n)=Θ(nlgn)$T(n)=\mathrm{\Theta }(nlgn)$

只要劃分是常數比例的，演算法的執行時間總是O(nlgn)$O(nlgn)$

。

隨機化快速排序

隨機演算法的思想

在前面分析快速排序的平均情況效能時，是建立在輸入資料的所有排列都是等概率的條件下的，但在實際工程中往往不會總出現這種良好的情況。

在【演算法】3 由招聘問題看隨機演算法中我們介紹了隨機演算法，它使得對於所有的輸入都有著較好的期望效能，因此隨機化快速排序在有大量資料輸入的情況下是一種更好的排序演算法。

以下是隨機化快速排序的好處：

1）其執行時間不依賴與輸入序列的順序

2）無需對輸入序列的分佈做任何假設

3）沒有 一種特別的輸入會引起最差的執行情況

4）最差的情況由隨機數產生器決定

隨機抽樣技術

現在我們來使用一種叫做隨機抽樣（random sampling）的隨機化技術，使用該技術就不再始終採用A[p]作為主元，而是從A[p…q]中隨機選擇一個元素作為主元。

為了達到這一目的，首先將A[p]$A[p]$

與從A[p...q]$A[p...q]$中隨機選出的一個元素交換。

通過對序列p...q$p...q$

的隨機抽樣，我們可以保證主元元素x=A[p]$x=A[p]$是等概率地從子陣列的q−p+1$q-p+1$個元素中選取的。

因為主元元素是隨機選擇的，我們可以期望在平均情況下對輸入陣列的劃分是比較均衡的。所以對前面的兩份虛擬碼做如下修改：

RANDOMIZED-PARTITION(A,p,q)
1   i=RANDOM(p,q)
2   exchange A[p] with A[i]
3   return PARTITION(A,p,q)

RANDOMIZED-QUICKSORT(A,p,q)
1   if p<q
2       r=RANDOMIZED-PARTITION(A,p,q)
3       RANDOMIZED-QUICKSORT(A,p,r-1)
4       RANDOMIZED-QUICKSORT(A,r+1,q)

有了隨機抽樣技術後再也不用擔心快速排序遇到最壞劃分的情況啦，所以說隨機化快速排序的期望執行時間是O(nlgn)$O(nlgn)$

。

實現示例

// Java
package com.nomasp;

import java.util.Random;

/**
 * Created by nomasp on 16/9/24.
 */
public class QuickSort {

    private int[] array;

    public QuickSort(int[] array) {
        this.array = array;
    }

    private void swap(int x, int y) {
        int tmp = array[x];
        array[x] = array[y];
        array[y] = tmp;
    }

    private int partition(int start, int end) {
        int pivot = array[start];
        int r = start;
        for (int i = start + 1; i <= end; i++) {
            if (array[i] <= pivot) {
                r += 1;
                swap(r, i);
            }
        }
        swap(start, r);
        return r;
    }

    private int randomizedPartition(int start, int end) {
        Random random = new Random();
        int i = start + random.nextInt(end - start);
        swap(start, i);
        return partition(start, end);
    }

    private void randomizedQuickSortCore(int start, int end) {
        if (start < end) {
            int r = randomizedPartition(start, end);
            randomizedQuickSortCore(start, r - 1);
            randomizedQuickSortCore(r + 1, end);
        }
    }

    public int[] quickSort() {
        randomizedQuickSortCore(0, array.length - 1);
        return array;
    }

    public int[] quickSort(int start, int end) {
        randomizedQuickSortCore(start, end);
        return array;
    }
}

---

---

感謝您的訪問，希望對您有所幫助。 歡迎大家關注、收藏以及評論。

---

為使本文得到斧正和提問，轉載請註明出處：
http://blog.csdn.net/nomasp

---