【演算法】4 五張圖帶你體會堆演算法

什麼是堆

堆（heap），是一類特殊的資料結構的統稱。它通常被看作一棵樹的陣列物件。在佇列中，排程程式反覆提取佇列中的第一個作業並執行，因為實際情況中某些時間較短的任務卻可能需要等待很長時間才能開始執行，或者某些不短小、但很重要的作業，同樣應當擁有優先權。而堆就是為了解決此類問題而設計的資料結構。

二叉堆是一種特殊的堆，二叉堆是完全二叉樹或者近似完全二叉樹，二叉堆滿足堆特性：父節點的鍵值總是保持固定的序關係於任何一個子節點的鍵值，且每個節點的左子樹和右子樹都是一個二叉堆。

當父節點的鍵值總是大於任何一個子節點的鍵值時為最大堆，當父節點的鍵值總是小於或等於任何一個子節點的鍵值時為最小堆。

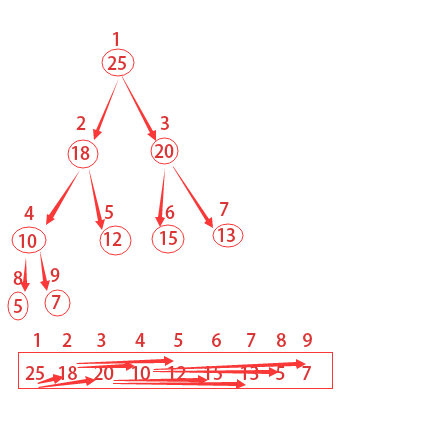
為了更加形象，我們常用帶數字的圓圈和線條來表示二叉堆等，但其實都是用陣列來表示的。如果根節點在陣列中的位置是1，第n個位置的子節點則分別在2n和2n+1位置上。

如下圖所描的，第2個位置的子節點在4和5，第4個位置的子節點在8和9。所以我們獲得父節點和子節點的方式如下：

PARENT(i)
1   return 小於或等於i/2的最大整數

LEFT-CHILD(i)
1   return 2i

RIGHT-CHILD(i)
1   return 2i+1

假定表示堆的陣列為A

，那麼A.length通常給出陣列元素的個數，A.heap−size表示有多少個堆元素儲存在該陣列中。這句話略帶拗口，也就是說陣列A[1...A.length]可能都有資料存放，但只有A[1...A.heap−size]中存放的資料才是堆中的有效資料。毫無疑問0≤A.heap−size≤A.length。

最大堆除了根以外所有結點i都滿足：A[PARENT(i)]≥A[i]

。

最小堆除了根以外所有結點i都滿足：A[PARENT(i)]≤A[i]

。

一個堆中結點的高度是該結點到葉借點最長簡單路徑上邊的數目，如上圖所示編號為4的結點的高度為1，編號為2的結點的高度為2，樹的高度就是3。

包含n個元素的隊可以看作一顆完全二叉樹，那麼該堆的高度是Θ(lgn)

。

通過MAX-HEAPIFY維護最大堆

程式中，不可能所有的堆都天生就是最大堆，為了更好的使用堆這一資料結構，我們可能要人為地構造最大堆。

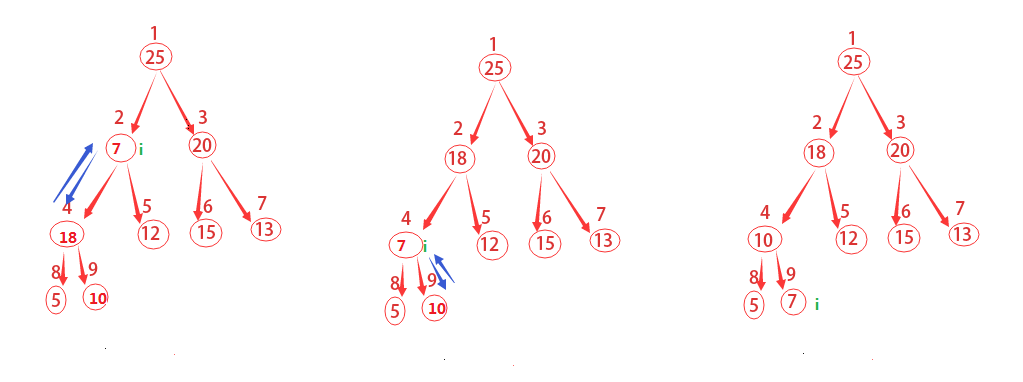
如何將一個雜亂排序的堆重新構造成最大堆，它的主要思路是：

從上往下，將父節點與子節點以此比較。如果父節點最大則進行下一步迴圈，如果子節點更大，則將子節點與父節點位置互換，並進行下一步迴圈。注意父節點要與兩個子節點都進行比較。

如上圖說描述的，這裡從結點為2開始做運算。先去l

為4，r為5，將其與父節點做比較，發現左子節點比父節點更大。因此將它們做交換，設4為最大的結點，並繼續以結點4開始做下一步運算。

因此可以給出虛擬碼如下：

MAX-HEAPIFY(A,i)
1   l=LEFT-CHILD(i)
2   r=RIGHT-CHILD(i)
3   if l<=A.heap-size and A[l]>A[i]
4       largest=l
5   else 
6       largest=i
7   if r<=A.heap-size and A[r]>A[largest]
8       largest=r
9   if largest != i
10      exchange A[i] with A[largest]
11      MAX-HEAPIFY(A,largest)      

在以上這些步驟中，調整A[i]、A[l]、A[r]的關係的時間代價為Θ(1)

，再加上一棵以i的子節點為根結點的子樹上執行MAX-HEAPIFY的時間代價（注意此處的遞迴不一定會發生，此處只是假設其發生）。因為每個子節點的子樹的大小至多為2n/3（最壞情況發生在樹的底層恰好半滿的時候）。因此MAX-HEAPIFY過程的執行時間為：

T(n)≤T(2n/3)+Θ(1)

也就是：

T(n)=O(lgn)

通過BUILD-MAX-HEAP構建最大堆

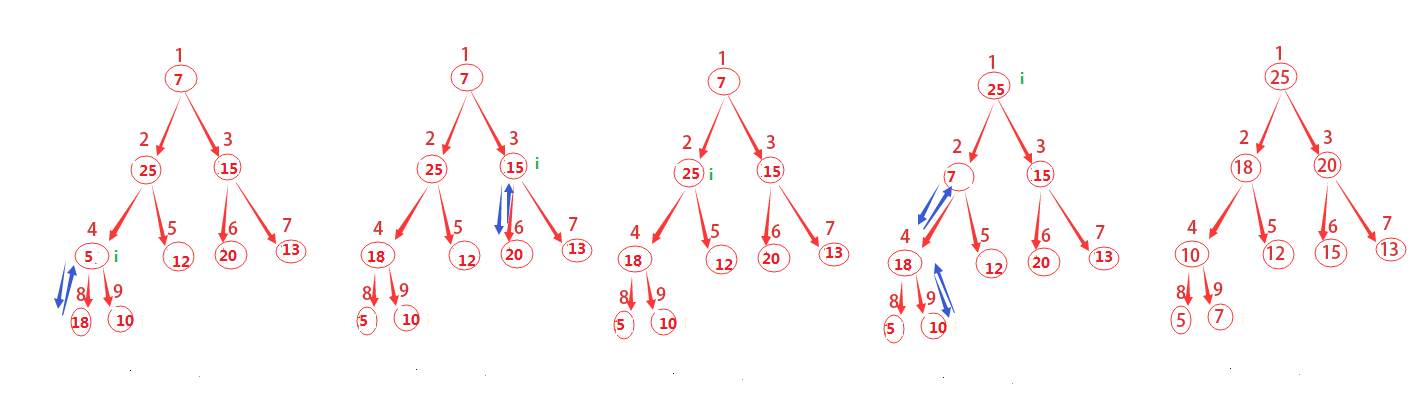
前面我們通過自頂向下的方式維護了一個最大堆，這裡將通過自底向上的方式通過MAX-HEAPIFY將一個n=A.length

的陣列A[1...n]轉換成最大堆。

回顧一下上面的圖示，其總共有9個結點，取小於或等於9/2的最大整數為4，從4+1，4+2，一直到n都是該樹的葉子結點，你發現了麼？這對任意n都是成立的哦。

因此這裡我們就要從4開始不斷的呼叫MAX-HEAPIFY(A,i)來構建最大堆。

為什麼會有這一思路呢？

原因是既然我們知道了哪些結點是葉子結點，從最後一個非葉子結點（這裡是4）開始，一次呼叫MAX-HEAPIFY函式，就會將該結點與葉子結點做相應的調整，這其實也就是一個遞迴的過程。

圖示已經這麼清晰了，就直接上虛擬碼咯。

BUILD-MAX-HEAP(A)
1   A.heap-size=A.length
2   for i=小於或等於A.length/2的最大整數 downto 1
3       MAX-HEAPIFY(A,i)

通過HEAPSORT進行堆排序演算法

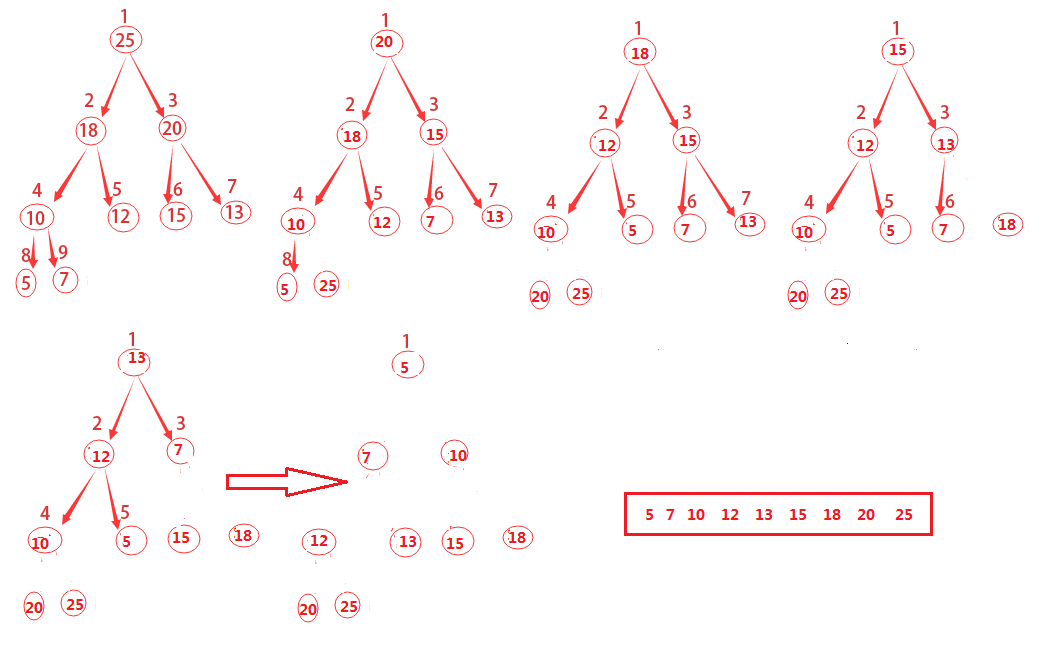
所謂的堆排序演算法，先通過前面的BUILD-MAX-HEAP將輸入陣列A[1...n]

建成最大堆，其中n=A.length。而陣列中的元素總在根結點A[1]中，通過把它與A[n]進行互換，就能將該元素放到正確的位置。

如何讓原來根的子結點仍然是最大堆呢，可以通過從堆中去掉結點n，而這可以通過減少A.heap−size

來間接的完成。但這樣一來新的根節點就違背了最大堆的性質，因此仍然需要呼叫MAX-HEAPIFY(A,1)，從而在A[1...n−1]上構造一個新的最大堆。

通過不斷重複這一過程，知道堆的大小從n−1

一直降到2即可。

上圖的演進方式主要有兩點：

1）將A[1]

和A[i]互換，i從A.length一直遞減到2

2）不斷呼叫MAX-HEAPIFY(A,1)對剩餘的整個堆進行重新構建

一直到最後堆已經不存在了。

HEAPSORT(A)
1   BUILD-MAX-HEAP(A)
2   for i=A.length downto 2
3       exchange A[1] with A[i]
4       A.heap-size=A.heap-size-1
5       MAX-HEAPIFY(A,1)

優先佇列

下一篇博文我們就會介紹大名鼎鼎的快排，快速排序啦，歡迎童鞋們預定哦~

話說堆排序雖然效能上不及快速排序，但作為一個盡心盡力的資料結構而言，其可謂業界良心吶。它還為我們提供了傳說中的“優先佇列”。

優先佇列（priority queue）和堆一樣，堆有最大堆和最小堆，優先佇列也有最大優先佇列和最小優先佇列。

優先佇列是一種用來維護由一組元素構成的集合S的資料結構，其中每個元素都有一個相關的值，稱之為關鍵字（key）。

一個最大優先佇列支援一下操作：

MAXIMUM(S)

：返回S中有著最大鍵值的元素。
EXTRACT−MAX(S)：去掉並返回S中的具有最大鍵字的元素。
INCREASE−KEY(S,x,a)：將元素x的關鍵字值增加到a，這裡假設a的值不小於x的原關鍵字值。
INSERT(S,x)：將元素x插入集合S中，這一操作等價於S=S∪{x}。

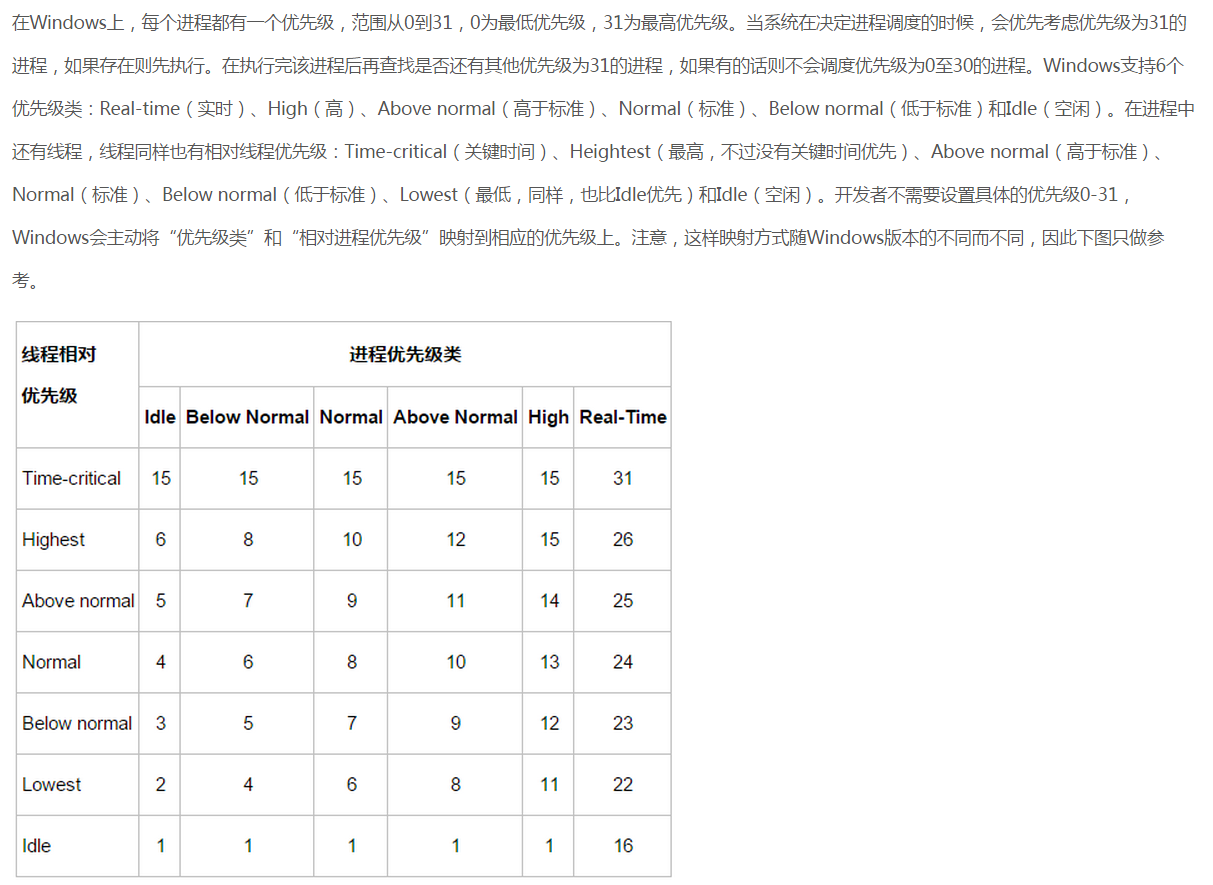
這裡來舉一個最大優先佇列的示例，我曾在關於“50% CPU 佔有率”題目的內容擴充套件 這篇博文中簡單介紹過Windows的系統程式機制。

這裡以圖片的形式簡單的貼出來如下：

在用堆實現優先佇列時，需要在堆中的每個元素裡儲存對應物件的控制程式碼（handle）。控制程式碼的準確含義依賴於具體的應用程式，可以是指標，也可以是整型數。

在堆的操作過程中，元素會改變其在陣列中的位置，因此在具體實現中，在重新確定堆元素位置時，就自然而然地需要改變其在陣列中的位置。

一、前面的MAXIMUM(S)

過程其實很簡單，完全可以在Θ(1)時間內完成，因為只需要返回陣列的第一個元素就可以呀，它已經是最大優先佇列了嘛。

HEAP-MAXIMUM(A)
1   return A[1]

二、EXTRACT−MAX(S)

就稍顯複雜了一點，它的時間複雜度是O(lgn)，因為這裡面除了MAX-HEAPIFY(A,1)以外，其他的操作都是常量時間的。

HEAP-EXTRACT-MAX(A)
1   if A.heap-size < 1
2       error "堆下溢"
3   max=A[1]
4   A[1]=A[A.heap-size]
5   A.heap-size=A.heap-size-1
6   MAX-HEAPIFY(A,1)
7   return max

三、INCREASE−KEY(S,x,a)

需要將一個大於元素x原有關鍵字值的a加到元素x上。

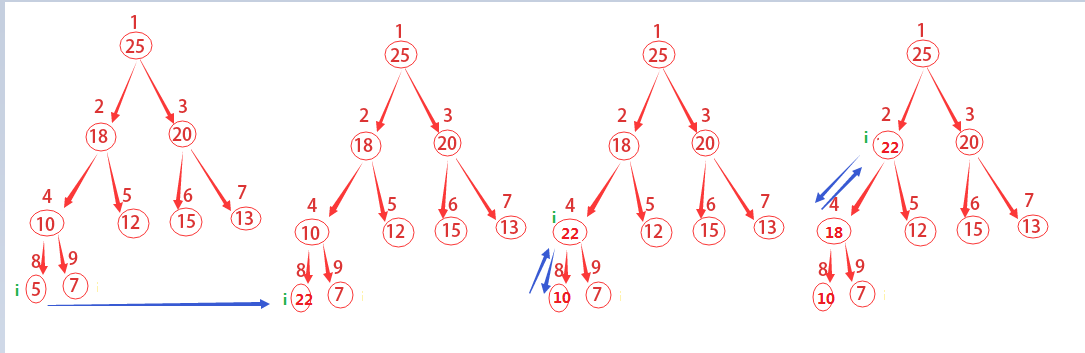
和上一個函式一樣，首先判斷a知否比原有的關鍵字更大。

然後就是老辦法了，不斷的將該結點與父結點做對比，如果父結點更小，那麼就將他們進行對換。

相信有圖示會更加清楚，於是……再來一張圖。

HEAP-INCREASE-KEY(A,i,key)
1   if key < A[i]
2       error "新關鍵字值比當前關鍵字值更小"
3   A[i]=key
4   while i>1 and A[PARENT(i)] < A[i]
5       exchange A[i] with A[PARENT(I)]
6       i=PARENT(i)

在包含n個元素的堆上，HEAP-INCREASE-KEY的執行時間就是O(lgn)了

。因為在第3行做了關鍵字更新的結點到根結點的路徑長度為O(lgn)。

四、INSERT(S,x)

首先通過一個特殊的關鍵字（比如這裡的-10000擴充套件）結點來擴充套件最大堆，然後呼叫HEAP-INCREASE-KEY來為新的結點設定對應的關鍵字，同時保持最大堆的性質。

MAX-HEAP-INSERT(A,key)
1   A.heap-size=A.heap-sieze+1
2   A[A.heap-size]=-10000
3   HEAP-INCREASE-KEY(A,A.hep-size,key)

在包含n個元素的堆上，MAX-HEAP-INSERT的執行時間就是O(lgn)了

。因為這個演算法相對於上一個演算法，除了HEAP-INCREASE-KEY之外就都是常量的執行時間了，而HEAP-INCREASE-KEY的執行時間我們在上一部分已經講過了。

總而言之，在一個包含n個元素的堆中，所有優先佇列的操作時間都不會大於O(lgn)

。

實現示例

updated at 2016/09/24

自己寫了demo，不過發現偉大的維基百科上有更棒的~

// C++
#include <iostream>
#include <algorithm>
using namespace std;

void max_heapify(int arr[], int start, int end) {
    //建立父節點指標和子節點指標
    int dad = start;
    int son = dad * 2 + 1;
    while (son <= end) { //若子節點指標在範圍內才做比較
        if (son + 1 <= end && arr[son] < arr[son + 1]) //先比較兩個子節點大小，選擇最大的
            son++;
        if (arr[dad] > arr[son]) //如果父節點大於子節點代表調整完畢，直接跳出函式
            return;
        else { //否則交換父子內容再繼續子節點和孫節點比較
            swap(arr[dad], arr[son]);
            dad = son;
            son = dad * 2 + 1;
        }
    }
}

void heap_sort(int arr[], int len) {
    //初始化，i從最後一個父節點開始調整
    for (int i = len / 2 - 1; i >= 0; i--)
        max_heapify(arr, i, len - 1);
    //先將第一個元素和已經排好的元素前一位做交換，再從新調整(剛調整的元素之前的元素)，直到排序完畢
    for (int i = len - 1; i > 0; i--) {
        swap(arr[0], arr[i]);
        max_heapify(arr, 0, i - 1);
    }
}

int main() {
    int arr[] = { 3, 5, 3, 0, 8, 6, 1, 5, 8, 6, 2, 4, 9, 4, 7, 0, 1, 8, 9, 7, 3, 1, 2, 5, 9, 7, 4, 0, 2, 6 };
    int len = (int) sizeof(arr) / sizeof(*arr);
    heap_sort(arr, len);
    for (int i = 0; i < len; i++)
        cout << arr[i] << ' ';
    cout << endl;
    return 0;
}

// Java
public class HeapSort {
    private static int[] sort = new int[]{1,0,10,20,3,5,6,4,9,8,12,17,34,11};
    public static void main(String[] args) {
        buildMaxHeapify(sort);
        heapSort(sort);
        print(sort);
    }

    private static void buildMaxHeapify(int[] data){
        //沒有子節點的才需要建立最大堆，從最後一個的父節點開始
        int startIndex = getParentIndex(data.length - 1);
        //從尾端開始建立最大堆，每次都是正確的堆
        for (int i = startIndex; i >= 0; i--) {
            maxHeapify(data, data.length, i);
        }
    }

    /**
     * 建立最大堆
     * @param data
     * @param heapSize需要建立最大堆的大小，一般在sort的時候用到，因為最多值放在末尾，末尾就不再歸入最大堆了
     * @param index當前需要建立最大堆的位置
     */
    private static void maxHeapify(int[] data, int heapSize, int index){
        // 當前點與左右子節點比較
        int left = getChildLeftIndex(index);
        int right = getChildRightIndex(index);

        int largest = index;
        if (left < heapSize && data[index] < data[left]) {
            largest = left;
        }
        if (right < heapSize && data[largest] < data[right]) {
            largest = right;
        }
        //得到最大值後可能需要交換，如果交換了，其子節點可能就不是最大堆了，需要重新調整
        if (largest != index) {
            int temp = data[index];
            data[index] = data[largest];
            data[largest] = temp;
            maxHeapify(data, heapSize, largest);
        }
    }

    /**
     * 排序，最大值放在末尾，data雖然是最大堆，在排序後就成了遞增的
     * @param data
     */
    private static void heapSort(int[] data) {
        //末尾與頭交換，交換後調整最大堆
        for (int i = data.length - 1; i > 0; i--) {
            int temp = data[0];
            data[0] = data[i];
            data[i] = temp;
            maxHeapify(data, i, 0);
        }
    }

    /**
     * 父節點位置
     * @param current
     * @return
     */
    private static int getParentIndex(int current){
        return (current - 1) >> 1;
    }

    /**
     * 左子節點position注意括號，加法優先順序更高
     * @param current
     * @return
     */
    private static int getChildLeftIndex(int current){
        return (current << 1) + 1;
    }

    /**
     * 右子節點position
     * @param current
     * @return
     */
    private static int getChildRightIndex(int current){
        return (current << 1) + 2;
    }

    private static void print(int[] data){
        int pre = -2;
        for (int i = 0; i < data.length; i++) {
            if (pre < (int)getLog(i+1)) {
                pre = (int)getLog(i+1);
                System.out.println();
            } 
            System.out.print(data[i] + " |");
        }
    }

    /**
     * 以2為底的對數
     * @param param
     * @return
     */
    private static double getLog(double param){
        return Math.log(param)/Math.log(2);
    }
}

---

---

感謝您的訪問，希望對您有所幫助。 歡迎大家關注、收藏以及評論。

---

為使本文得到斧正和提問，轉載請註明出處：
http://blog.csdn.net/nomasp

---