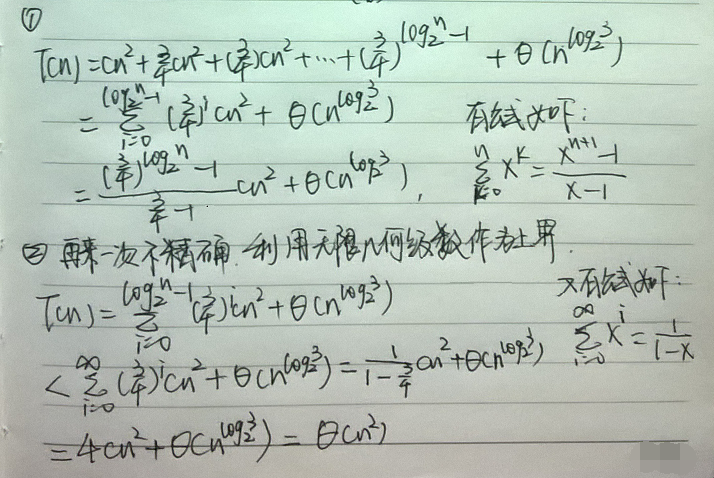【演算法】2 由股票收益問題再看分治演算法和遞迴式

nomasp發表於2015-05-27
演算法遞迴

回顧分治演算法

分治演算法的英文名叫做“divide and conquer”，它的意思是將一塊領土分解為若干塊小部分，然後一塊塊的佔領征服，讓它們彼此異化。這就是英國人的軍事策略，但我們今天要看的是演算法。

如前所述，分治演算法有3步，在上一篇中已有介紹，它們對應的英文名分別是：divide、conquer、combine。

接下來我們通過多個小演算法來深化對分治演算法的理解。

二分查詢演算法

問題描述：在已排序的陣列A中查詢是否存在數字n。

1）分：取得陣列A中的中間數，並將其與n比較
2）治：假設陣列為遞增陣列，若n比中間數小，則在陣列左半部分繼續遞迴查詢執行“分”步驟
3）組合：由於在陣列A中找到n後便直接返回了，因此這一步就無足輕重了

平方演算法

問題描述：計算x的n次方

我們有原始演算法：用x乘以x，再乘以x，再乘以x，一直有n個x相乘

這樣一來演算法的複雜度就是Θ(n)

\Theta(n)
。

分治演算法：我們可以將n一分為二，於是，

當n為奇數時，xn=x(n−1)/2∗x(n−1)/2∗x

x^n=x^{(n-1)/2}*x^{(n-1)/2}*x

當x為偶數時，xn=xn/2∗xn/2

x^n=x^{n/2}*x^{n/2}

此時的複雜度就變成了Θ(lgn)

\Theta(lgn)
。

斐波那契數

斐波那契數的定義如下：

f0=0
f_0 = 0

f1=1
f_1 = 1

fi=fi−1+fi−2(i>1)
f_i = f_{i-1}+f_{i-2} (i > 1)

當然，可以直接用遞迴來求解，但是這樣一來花費的時間就是指數級的Ω(Φn)

\Omega(\Phi ^n)
，Φ
\Phi
為黃金分割數。

然後我們可以更進一步讓其為多項式時間。

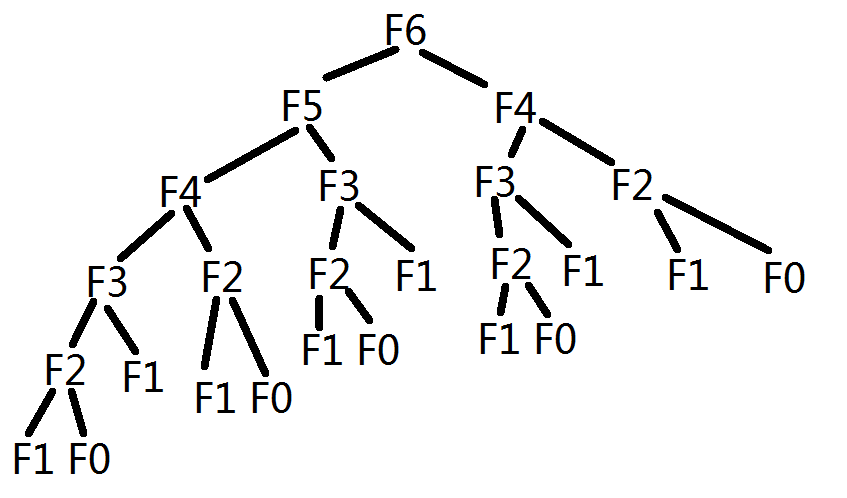
這裡寫圖片描述

上面這幅圖雖然比較簡略，在求n為6時的斐波那契數，我們卻求解了3次F3，F1和F0的求解次數則更多了，我們完全可以讓其只求解一次。

對此，還有一個計算公式：

Fi=Φi−Φ⎯⎯i(√5)

F_i=\frac{\Phi^i-\overline\Phi^i}{\sqrt(5)}

其中Φ⎯⎯⎯

\overline\Phi
是黃金分割率Φ
\Phi
的共軛數。

然後這個公式只存在與理論中，在當今計算機中仍舊無法計算，因為我們只能使用浮點型，而浮點型都有一定的精度，最後計算的時候鐵定了會丟失一些精度的。

下面再介紹一種平方遞迴演算法：

這裡寫圖片描述

一時忘了矩陣怎麼計算乘機，感謝@fireworkpark 相助。

最大子陣列問題

最近有一個比較火的話題，股票，那麼這一篇就由此引入來進一步學習分治演算法。在上一篇部落格中已經對插入排序和歸併排序做了初步的介紹，大家可以看看：【演算法基礎】由插入排序看如何分析和設計演算法

當然了，這篇部落格主要用來介紹演算法而非講解股票，所以這裡已經有了股票的價格，如下所示。

天 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
股票價格 50 57 65 75 67 60 54 51 48 44 47 43 56 64 71 65 61 73 70
價格波動 0 7 8 18 -8 -7 -6 -3 -3 -4 3 -4 13 10 7 -6 -4 12 -3

價格表已經有了問題是從哪一天買進、哪一天賣出會使得收益最高呢？你可以認為在價格最低的時候買入，在價格最高的時候賣出，這是對的，但不一定任何時候都適用。在這裡的價格表中，股票價格最高的時候是第3天、價格最低的時候是第11天，怎麼辦？讓時間反向行駛？

就像我以前參加學校裡的程式設計競賽時一樣，也可以用多個for迴圈不斷的進行比較。這裡就是將每對可能的買進和賣出日期進行組合，只要賣出日期在買進日期之前就好，這樣在18天中就有C218

C_{18}^2
種日期組合，也可以寫成(182)
(_2^{18})
。因此對於n
n
天，就有(n2)
(_2^n)
種組合，而(n2)=Θ(n2)
(_2^n)=\Theta(n^2)
，另外處理每對日期所花費的時間至少也是常量，因此這種方法的執行時間為Ω(n2)
\Omega(n^2)
。

然後，我們在學習演算法，自然要以演算法的角度來看這個問題。比起股票價格，我們更應該關注價格波動。如果將這個波動定義為陣列A，那麼問題就轉換為尋找A的和最大的非空連續子陣列。這種連續子陣列就是標題中的最大子陣列（maximum subarray）。將原表簡化如下：

陣列 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
A 7 8 18 -8 -7 -6 -3 -3 -4 3 -4 13 10 7 -6 -4 12 -3

在這個演算法中，常常被說成是“一個最大子陣列”而不是“最大子陣列”，因為可能有多個子陣列達到最大和。

只有當陣列中包含負數時，最大子陣列問題才有意義。如果所有陣列元素都是非負的，最大子陣列問題沒有任何難度，因為整個陣列的和肯定是最大的。

使用分治思想解決問題

我們將實際問題轉換為演算法問題，在這裡也就是要尋找子陣列A[low...high]

A[low...high]
的最大子陣列。分治思想意味著將問題一分為二，這裡就需要找到陣列的中間位置mid
mid
，然後考慮求解2個子陣列A[low...mid]
A[low...mid]
和A[mid+1...high]
A[mid+1...high]
。而A[low...high]
A[low...high]
的任何連續子陣列A[i...j]
A[i...j]
所處的位置必然是以下情況之一：

1）完全位於子陣列A[low...mid]

A[low...mid]
中，因此low≤i≤j≤mid
low\leq i\leq j \leq mid
；
2）完全位於子陣列A[mid+1...high]
A[mid+1...high]
中，因此mid<i≤j≤high
mid<i\leq j\leq high
；
3）跨越中點mid
mid
，因此low≤i≤mid≤j≤high
low\leq i\leq mid\leq j\leq high
。

A[low...high]

A[low...high]
的一個最大子陣列所處的位置必然是這三種情況之一，而且還是這三種情況中所有子陣列中和最大者。對於第1種和第2種情況我們可以通過遞迴來求解最大子陣列，對於第三種情況我們可以通過下面虛擬碼所示來求解。

FIND-MAX-CROSSING-SUBARRAY(A,low,mid,high)
1   left-sum = -10000
2   sum = 0
3   for i = mid downto low
4        sum = sum + A[i]
5        if sum > left-sum
6             left-sum = sum
7             max-left = i
8   right-sum = -10000
9   sum = 0
10  for j = mid + 1 to high
11       sum = sum + A[i]
12       if sum > right-sum
13            right-sum = sum
14            max-right = j
15   return (max-left, max-right, left-sum + right-sum)

下面是以上程式的一個簡易程式。

#include <iostream>
#include <cstdio>

using namespace std;

int const n=18;
int A[n]={7,8,18,-8,-7,-6,-3,-3,-4,3,-4,13,10,7,-6,-4,12,-3};
int B[3];
int low,high,mid;
int max_left,max_right;
int sum;

void find_max_crossing_subarray(int A[],int low,int mid,int high);

int main()
{
    find_max_crossing_subarray(A,0,7,15);
    for(int i=0;i<3;i++)
    {
        printf("%d ",B[i]);
    }
    return 0;
}

void find_max_crossing_subarray(int A[],int low,int mid,int high)
{
   int left_sum=-10000;
   sum=0;
   for(int i=mid;i>=low;i--)
   {
       sum=sum+A[i];
       if(sum>left_sum)
       {
           left_sum=sum;
           max_left=i;
       }
   }
   int right_sum=-10000;
   sum=0;
   for(int j=mid+1;j<=high;j++)
   {
       sum=sum+A[j];
       if(sum>right_sum)
       {
           right_sum=sum;
           max_right=j;
       }
   }
   B[0]=max_left;
   B[1]=max_right;
   B[2]=left_sum+right_sum;
}

如果子陣列A[low...high]

A[low...high]
包含n個元素（即n=high−low+1
n=high-low+1
），則呼叫FIND-MAX-CROSSING-SUBARRAY(A,low,mid,high)花費Θ(n)
\Theta(n)
時間。而上面的兩個for迴圈都次迭代都會花費Θ(1)
\Theta(1)
時間，每個for迴圈都執行了mid−low+1
mid-low+1
（或high−mid
high-mid
）次迭代，因此總迴圈的迭代次數為：

(mid−low+1)+(high−mid)=high−low+1=n

(mid-low+1)+(high-mid)=high-low+1=n

可以看出上面的演算法所花費的時間是線性的，這樣我們就可以來求解最大子陣列問題的分治演算法的虛擬碼咯：

FIND-MAXIMUM-SUBARRAY(A,low,high)
1   if high==low
2        return (low,high,A[low])
4        (left-low,left-high,left-sum)=FIND-MAXIMUM-SUBARRAY(A,low,mid)
5        (right-low,right-high,right-sum)=FIND-MAXIMUM-SUBARRAY(A,mid+1,high)
6        (cross-low,cross-high,cross-sum)=FIND-MAX-CROSSING-SUBARRAY(A,low,mid,high)
7        if left-sum>=right-sum and left-sum>=cross-sum)
              return (left-low,left-high,left-sum)
8        else if(right-sum>=left-sum and right-sum>=cross-sum)
              return (right-low,right-high,right-sum)
9        else return (cross-low,cross-high,cross-sum)

只要初始呼叫FIND-MAXIMUM-SUBARRAY(A,1,A.length)就可以求出A[1...n]

A[1...n]
的最大子陣列了。

分析分治演算法和漸近記號中的省略問題

下面我們又來使用遞迴式來求解前面的遞迴過程FIND-MAXIMUM-SUBARRAY的執行時間了，就像上一篇分析歸併排序那樣，對問題進行簡化，假設原問題的規模為2的冪，這樣所有子陣列的規模均為整數。

第1行花費常量時間。當n=1時，直接在第二行return後跳出函式，因此

T(1)=Θ(1)

T(1)=\Theta(1)

當n>1時，為遞迴情況。第1行和第3行都花費常量時間，第4行和第5行求解的子問題均為n/2個元素的子陣列，因此每個子問題的求解總執行時間增加了2T(n/2)。第6行呼叫FIND-MAX-CROSSING-SUBARRAY花費Θ(n)

\Theta(n)
時間，第7行花費Θ(1)
\Theta(1)
時間，因此總時間為

T(n)=Θ(1)+2T(n/2)+Θ(n)+Θ(1)=2T(n/2)+Θ(n)

T(n)=\Theta(1)+2T(n/2)+\Theta(n)+\Theta(1)=2T(n/2)+\Theta(n)

在上面的步驟中，將Θ(1)

\Theta(1)
省略掉的作法大家應該都理解吧。

回顧前面n=1的情況，第一行花費了常量時間，第二行同樣也花費了常量時間，但這兩步花費的總時間卻是Θ(1)

\Theta(1)
而非2Θ(1)
2\Theta(1)
，這是因為在Θ
\Theta
符號中已經包含了常數2在內了。

但是為什麼第4行和第5行中卻是2Θ(n/2)

2\Theta(n/2)
而非Θ(n/2)
\Theta(n/2)
時間呢？因為這裡是遞迴呀，這裡的因子就決定了遞迴樹種每個結點的孩子個數，因子為2就意味著這是一顆二叉樹（也就是每個結點下有2個子節點）。

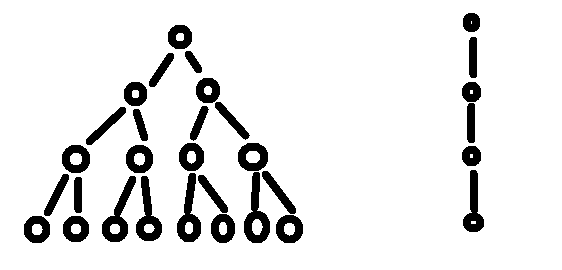
如果省略了這個因子2會發生什麼呢？不要以為就是一個2這麼小的數而已哦，後果可嚴重了，看下圖……左側是一棵4層的樹，右側就是因子為1的樹（它已經是線性結構了）。

這裡寫圖片描述

總結來說，漸近記號都包含了常量因子，但遞迴符號卻不包含它們。

藉助遞迴樹求解遞迴式

前面我們已經看到了遞迴式，也看到了遞迴樹，那麼如何藉助遞迴樹來求解遞迴式呢？接下來就來看看吧。

在遞迴樹中，每個結點都表示一個單一問題的代價，子問題對應某次遞迴函式呼叫。

通過對樹中每層的代價進行求和，就可以得到每層的代價；然後將所有層的代價求和，就可以得要到所有層次的遞迴呼叫的總代價。

我們通常用遞迴樹來得出一個較好的猜測結果，然後用代入法來證明猜測是否正確。但是通過遞迴樹來得到結果時，不可避免的要忍受一些”不精確“，得在稍後才能驗證猜測是否正確。

因為下面的示例圖太難用鍵盤敲出來了，我就用了手寫，希望大家不介意。

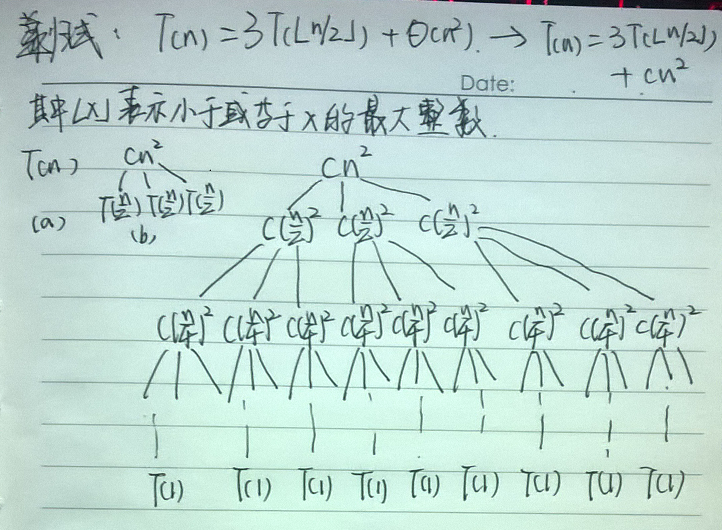
這裡寫圖片描述

如下所示，有一個遞迴式，我們要藉助它的遞迴樹來求解最終的結果。前面所說的忍受“不精確”這裡就有2點：

1）我們要關注的更應該是解的上界，因為我們知道舍入對求解遞迴式沒有影響，因此可以將Θ(n2)

\Theta(n^2)
寫成cn2
cn^2
，且為該遞迴式建立瞭如下遞迴樹。

2）我們還將n

n
假定為2的冪，這樣所有子問題的規模均為正數。

圖a所示的是T(n)

T(n)
，在圖b中則得到了一步擴充套件的機會。它是如何分裂的呢？遞迴式的係數為3，因此有3個子結點；n被分為2部分，因此每個結點的耗時為T(n/2)
T(n/2)
。圖c所示的則是更加進一步的擴充套件，且直到最後的終點。

這棵樹有多高（深）呢？

我們發現對於深度為i

i
的結點，相應的規模為n/2i
n/2^i
。因此當n/2i=1
n/2^i=1
時，也就意味著等式i=log2n
i=\log_2 n
成立，此時子問題的規模為1。因此這個遞迴樹有log2n+1
\log_2 n+1
層。那為什麼不是log2n
\log_2 n
層呢？因為深度從0
0
開始，也就是(0,1,2,...,log2n)
(0,1,2,...,\log_2 n)
。

有了深度還需要計算每一層的代價。其中每層的結點數都是上一層的3倍，因此深度為i

i
的結點數為3i
3^i
。而每一層的規模都是上一層的1/4
1/4
，所以對於i=0,1,2,...,log4n−1
i=0,1,2,...,\log_4 n -1
，深度為i
i
的每個結點的代價為c(n/2i)2
c(n/2^i)^2
。

因此對於i=0,1,2,...,log4n−1

i=0,1,2,...,\log_4 n -1
，深度為i
i
的所有結點的總代價為(3i)∗(c(n/2i)2)
(3^i)*(c(n/2^i)^2)
，也就是3ic(n/2i)2
3^ic(n/2^i)^2
。

遞迴樹的最底層深度為log2n

\log_2 n
，它有3log2n=nlog23
3^{\log_2 n}=n^{log_2 3}
個結點，每個結點的代價為T(1)
T(1)
，總代價就是nlog23T(1)
n^{log_2 3}T(1)
，假定T(1)
T(1)
為常量，即為Θ(nlog23)
\Theta(n^{log_2 3})
。

這裡寫圖片描述

至於這最後的4c

4c
為什麼可以直接省略掉，如上一節所說的，漸近記號都包含了常量因子。因此猜測T(n)=Θ(n2)
T(n)=\Theta(n^2)
。在這個示例中，cn2
cn^2
的係數形成了一個遞減幾何級數。由於根結點對總代價的貢獻為cn2
cn^2
，所以根結點的代價佔總代價的一個常量比例，也就是說，根結點的代價支配了整棵樹的總代價。

這裡寫圖片描述

不知道大家看不看得清，上面的兩行文字是“我們要證的是T(n)≤dn2

T(n)\leq dn^2
對某個常量d>0
d>0
成立，使用常量c>0
c>0
“和”當d≥4c
d \geq 4c
時，最後一步成立。

寫一篇部落格本來不會這麼漫長的，可是這是演算法，結果就不一樣了……

感謝您的訪問，希望對您有所幫助。 歡迎大家關注、收藏以及評論。

為使本文得到斧正和提問，轉載請註明出處：
http://blog.csdn.net/nomasp

相關文章