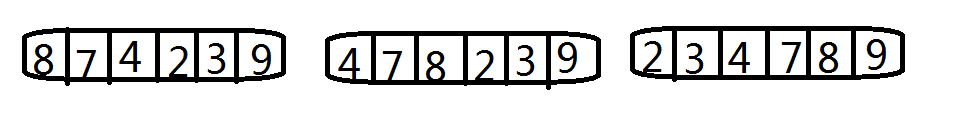【演算法】1 由插入排序看如何分析和設計演算法

nomasp發表於2015-07-01
演算法排序

插入排序及其解決思路

演算法的作用自然不用多說，無論是在校學生，還是已經工作多年，只要想在計算機這條道路走得更遠，演算法都是必不可少的。

就像程式語言中的“Hello World！”程式一般，學習演算法一開始學的便是排序演算法。排序問題在日常生活中也是很常見的，說得專業點：

輸入是：n個數的一個序列<a1,a2,...,an−1,an>

<a_1,a_2,...,a_{n-1},a_n>

輸出是：這n個數的一個全新的序列<a,1,a,2,...,a,n−1,a,n>
<a_1^,,a_2^,,...,a_{n-1}^,,a_n^,>
，其特徵是a,1≤a,2≤...≤a,n−1≤a,n
a_1^, \leq a_2^, \leq ... \leq a_{n-1}^, \leq a_n^,

舉個例子，在本科階段學校往往要求做的實驗中大多是“學生管理系統”、“資訊管理系統”、“圖書管理系統”這些。就比如“學生管理系統”中的分數，每當往裡面新增一個新的分數時，便會和其他的進行比較從而得到由高到低或由低到高的排序。

我本人是不太喜歡做這種管理系統的…… 再舉個比較有意思的例子。

大家肯定都玩過撲克牌，撇開部分人不說，相信大部分童鞋都熱衷於將牌按序號排好。那麼這其中就蘊含著演算法的思想：

  • 1）手中的撲克牌有2種可能：沒有撲克牌（為空）或者有撲克牌且已排好序。
  • 2）從桌上抓起一張牌後，從左往右（從右往左）依次進行比較，最終選擇一個合適的位置插入。

簡單的說，插入排序的精髓在於“逐個比較”。

在列出程式碼之前，先來看看下面的第一張圖，我畫的不是太好，就是有沒有經過排序的 “8，7，4，2，3，9”幾個數字，根據上面的描述，將排序過程描述為：

  • 1）將第二個數字“7”和“8”比較，發現7更小，於是將“8”賦值到“7”所在的位置，然後將7賦值給“8”所在的位置。
  • 2）將”4“移到”7“所在的位置，”7“和”8“後移一位。
  • 3）同樣的步驟，將”2“和”3“移到”4“的前面。
  • 4）”9“比前面的數字都大，故不移動。

這裡寫圖片描述

僅僅是這樣的描述還是不夠的，我們需要更加專業一點。

  • 1）設定一個迴圈，從第二個數字開始（索引為1）不斷與前面的數字相比。
  • 2）每次迴圈開始時作為比較的數的索引為j，設定temp為其值。（因為在前面也看到了，將”8“賦值到”7“的位置時，如果不將”7“儲存起來，那麼便丟失了這個數字。）
  • 3）取得j的前一位i。
  • 4）只要i仍在陣列中，並且索引為i處的值大於temp，就將i後一位的值設為i處的值，同時將i減1。
  • 5）在i不在陣列中或i處的值不必temp大時結束第四部的迴圈，然後將i後一位的值設定為temp。

將上面這部分描述翻譯為insertion_sort函式，下面是完整的測試程式。

// C Plus Plus
// A是陣列，j是遍歷整個陣列的索引，temp是每次取出來作比較的值
void insertion_sort() {
    for(int j = 1; j < n; j++) {
        int temp = A[j];
        int i = j-1;
        while (i >= 0 && A[i] > temp) {
            A[i+1] = A[i];
            i = i-1;
        }
        A[i+1] = temp;
    }
}
updated at 2016/09/24

// Java
    public int[] insertion(int[] nums) {
        for (int i = 1; i < nums.length; i++) {
            int tmp = nums[i];
            int prev = i - 1;
            while (prev >= 0 && nums[prev] > tmp) {
                nums[prev + 1] = nums[prev];
                prev -= 1;
            }
            nums[prev + 1] = tmp;
        }
        return nums;
    }

下面是能夠幫助我們理解演算法的正確性的迴圈不變式的三條性質：

初始化：迴圈第一次迭代之前，它為真。
保持：如果迴圈的某次迭代之前它為真，那麼下次迭代之前它仍為真。
終止：在迴圈終止時，不變式能夠提供一個有助於證明演算法正確性的性質。

就比如上面排序的例子，終止意味著在最後一次迭代時，由傳入陣列元素構成的子陣列元素都已排好序，因此此時子陣列就等同與原陣列，於是迴圈終止。

學習如何分析演算法

繼續分析排序演算法，我們知道排序10000個數肯定要比排序10個數所花費的時間更長，但除了輸入的項數外就沒有其他的影響因素嗎？當然有，比如說輸入的序列的已被排序的程度，如果是“23456781”這個序列，我們僅僅需要將1放到首位就好，而輸入是”87654321“，我們就需要將7到1依次與其前面的數字進行比較。

關於演算法的分析也有兩個定義：

1）輸入規模，當考慮的是排序演算法時，那麼規模就指的是項數；如果考慮的是圖演算法，那麼規模就是頂點數和邊數。
2）執行時間，名義上來說就是演算法執行的時間，但實際上我們在分析一個演算法時考量的演算法執行的運算元或步數。

下面我們通過前面排序演算法的虛擬碼來分析它的執行時間。

INSERTION-SORT(A)
1   for j = 2 to A.length                  // 代價c1，次數n   
2       temp=A[j];                         // 代價c2，次數n-1
3       // 將A[j]插入到已排序的A[1..j-1]      // 代價0，次數n-1
4       i=j-1;                             // 代價c4，次數n-1
5       while i>0 and A[i]>temp            // 代價c5  
6           A[i+1]=A[i];                   // 代價c6
7           i=i-1;                         // 代價c7       
8       A[i+1]=temp;                       // 代價c8，次數n-1

代價為c1處的次數為n應該比較好理解對吧，從j=1到j=n一共有n步，j=n也應該包括在內，因為這是演算法終止的情況。而j=n時，程式直接終止了，所以在代價c2、c3、c7處次數都為n-1。

那麼在while迴圈中呢，代價為c4的時候次數為多少呢，很顯然應該是∑nj=2tj

\sum_{j=2}^{n} t_j
，而c5和c6在while迴圈裡總有一次它不會去執行，因此次數為∑nj=2(tj−1)
\sum_{j=2}^{n} (t_j-1)
。

將代價和次數相乘，便得到了該演算法所需的總時間：
T(n)=c1n+c2(n−1)+c4(n−1)+c5∑nj=2tj+c6∑nj=2(tj−1)+c7∑nj=2(tj−1)+c8(n−1)

T(n)=c_1n+c_2(n-1)+c_4(n-1)+c5\sum_{j=2}^{n} t_j+c_6\sum_{j=2}^{n} (t_j-1)+c_7\sum_{j=2}^{n} (t_j-1)+c_8(n-1)

除此之外我們還可以來對演算法進行最好和最壞情況的分析：
1）在最好情況下，也就是整個輸入陣列其實都是排好序的，那麼它根本沒法進入while迴圈，也就是說當i取初值j-1時，有A[i]≤temp

A[i]\leq temp
，從而對j=2,3,4...n
j=2,3,4...n
都有tj=1
t_j=1
。

那麼演算法的總時間也就可以算出來了：
T(n)=(c1+c2+c4+c5+c8)n−(c2+c4+c5+c8)

T(n)=(c_1+c_2+c_4+c_5+c_8)n-(c_2+c_4+c_5+c_8)

2）在最壞情況下，也就是陣列是逆向排好序的，那麼就需要將A[j]

A[j]
與已排好序的陣列A[1...j1]
A[1...j_1]
中的每個元素進行比較，從而對j=2,3,4...n
j=2,3,4...n
都有tj=j
t_j=j
。

那麼演算法的總時間也就可以算出來了：
T(n)=(c52+c62+c72)n2+(c1+c2+c4+c52−c62−c72+c8)n−(c2+c4+c5+c8)

T(n)=(\frac{c_5}{2}+\frac{c_6}{2}+\frac{c_7}{2})n^2+(c_1+c_2+c_4+\frac{c_5}{2}-\frac{c_6}{2}-\frac{c_7}{2}+c_8)n-(c_2+c_4+c_5+c_8)

漸近記號

Θ

\Theta

在上面我已經求出了該排序演算法的執行總時間，但我們可以對其做進一步的簡化以及抽象，我們只考慮最壞情況，因為在實際中它更有意義。將執行時間表示為an2+bn+c

an^2+bn+c
，其中的a、b、c
a、b、c
都依賴於ci
c_i
。

讓我們來做進一步的抽象，通過只考慮執行時間的增長率和增長量級。因為當程式足夠大時，低階項便不再重要了，甚至連高階項的係數也可以忽略不計。於是，我們記插入排序在最壞情況下所需要的執行時間為Θ(n2)

\Theta(n^2)
。

現在是時候給出Θ

\Theta
的定義了：
Θ(g(n))={f(n):存在正數常量c1、c2和n0，使得對所有的n≥n0,有0≤c1g(n)≤f(n)≤c2g(n)}
\Theta(g(n))=\{f(n):存在正數常量c_1、c_2和n_0，使得對所有的n\geq n_0,有0 \leq c_1g(n) \leq f(n) \leq c_2g(n)\}

也就是說在跨過n0

n_0
之後，f(n)
f(n)
就一直處於c1g(n)
c_1g(n)
和c2g(n)
c_2g(n)
之間，其中c1g(n)
c_1g(n)
是下界，c2g(n)
c_2g(n)
是上界。

O

O
和Ω
\Omega

O

O
和Θ
\Theta
相比，前者就只是後者的一半——只有漸近上界，而沒有漸近下界。那麼它的定義為：
O(g(n))={f(n):存在正數常量c和n0，使得對所有的n≥n0,有0≤f(n)≤cg(n)}
O(g(n))=\{f(n):存在正數常量c和n_0，使得對所有的n\geq n_0,有0 \leq f(n) \leq cg(n)\}

Ω

\Omega
和Θ
\Theta
相比，前者就只是後者的一半——只有漸近下界，而沒有漸近下界。那麼它的定義為：
Ω(g(n))={f(n):存在正數常量c和n0，使得對所有的n≥n0,有0≤f(n)cg(n)≤cg(n)}
\Omega(g(n))=\{f(n):存在正數常量c和n_0，使得對所有的n\geq n_0,有0 \leq f(n)cg(n) \leq cg(n) \}

設計分治演算法

前面的排序問題使用的方法叫做增量法，即在排序子陣列A[1...j−1]

A[1...j-1]
後，將單個元素A[j]
A[j]
插入到子陣列的適當位置，然後引數排序好的陣列A[1...j]
A[1...j]
，它的精髓在於“逐個比較”。

現在我們再來介紹一種新的方法，叫做分治法，它同樣也是鼎鼎大名。它的精髓在於“一分為二“，而驅動這個演算法的這是遞迴。

分治演算法在每層遞迴中都有三個步驟：

  • 1）分解原問題為若干子問題，這些子問題是縮小版的原問題。（抽象的講，將一個已經切成楔形的大塊西瓜可以再切成多個小的楔形西瓜。）
  • 2）解決這些子問題，遞迴地求解各個子問題。然後，若問題的規模足夠小，則直接求解。（繼續舉例子，要吃完一大塊西瓜，可以不斷的吃小部分，當西瓜塊足夠小時，可以一口乾掉。）
  • 3）合併這些子問題的解成原問題的解。（吃完的那些小塊西瓜加在一起就是剛才那一塊很大的西瓜了。）

雖然西瓜的例子能夠體現分治演算法的思想，但用前面的撲克牌來演示則更加合適，畢竟它有數字呀。來來來，想象一下，桌上正有兩堆牌，且分別都已經排號順序，可是呢我們需要這兩堆牌合併起來並且排序好。

那麼怎麼操作呢？很簡單，一句話就能說清楚：不斷從兩堆牌的頂上選取較小的一張，然後放到新的撲克牌堆中。

首先我們將撲克牌定義成陣列A

A
，p
p
和q
q
以及r
r
都是陣列的下標，且p≤q<r
p \leq q < r
，兩段已排序好的子陣列是A[p..q]
A[p..q]
和A[q+1..r]
A[q+1..r]
，我們需要做的是將其排序為A[p..r]
A[p..r]
。下面的虛擬碼便實現了這個思想：

MERGE(A,p,q,r)
1  n1 = (q - p) + 1 = q - p + 1
2  n2 = (r - (q + 1)) +1 = r - q
3  let L[1..n1+1] and R[1..n2+1] be new arrays
4  for i = 1 to n1
5      L[i] = A[p + i -1]
6  for j = 1 to n2
7      R[j] = A[q + j]
8  L[n1 + 1] = #
9  R[n2 + 1] = #
10 i = 1;
11 j = 1;
12 for k = p to r
13     if L[i] 小於等於 R[j]
14        A[k] = L[i];
15        i = i + 1;
16     else 
17        A[k] = R[j]
18        j = j + 1;

上面的”# “號就是傳說中的哨兵牌，每當顯露一張哨兵牌時，它不可能為較小的值，除非兩個堆都已顯露出哨兵牌。但是出現這種情況就意味著演算法結束，所有非哨兵牌都已被放置到輸出堆。

………………p     q       r………………
………………3 6 8 9 2 5 7 8………………
        k

L 3 6 8 9 #     R 2 5 7 8 #
  i               j

比較”3“和”2“，發現2更小，於是將2放到A陣列的首位，並且將j

j
移後一位。

………………p     q       r………………
………………2 6 8 9 2 5 7 8………………
          k

L 3 6 8 9 #     R 2 5 7 8 #
  i                 j

比較”3“和”5“，發現3更小，於是將3放到陣列A的首位，並且將i

i
移後一位。

………………p     q       r………………
………………2 3 8 9 2 5 7 8………………
            k

L 3 6 8 9 #      R 2 5 7 8 #
    i                j

以此類推，最終A陣列就成排好了序……

………………p     q       r………………
………………2 3 5 6 7 8 8 9………………
                      k

L 3 6 8 9 #      R 2 5 7 8 #    
          i                j

將上面的思想以及虛擬碼寫成如下程式，大家可以參考參考：

#include <iostream>
#include <cstdio>

using namespace std;

#define MAX_N 1000

int A[MAX_N];
int L[MAX_N/2];
int R[MAX_N/2];
int n,p,q,r;

void merge();

int main()
{
    printf("陣列長度：\n");
    scanf("%d",&n);
    printf("陣列內容：\n");
    for(int i=0;i<n;i++)
    {
        scanf("%d",&A[i]);
    }
    printf("輸入p q r\n");\
    scanf("%d %d %d",&p,&q,&r);
    merge();

    for(int i=0;i<n;i++)
    {
        printf("%d ",A[i]);
    }
    return 0;
}

void merge()
{
    int n1=q-p+1;
    int n2=r-q;
    for(int i=0;i<n1;i++)
        L[i]=A[p+i];
    for(int j=0;j<n2;j++)
        R[j]=A[q+j+1];
    L[n1]=100;
    R[n2]=100;
    for(int k=p,i=0,j=0;k<=r;k++)
    {
        if(L[i]<=R[j])
        {
            A[k]=L[i];
            i=i+1;
        }
        else
        {
            A[k]=R[j];
            j=j+1;
        }
    }
}

下面沒有用圖示而是用了程式碼顯示塊來顯示，應該也能看的吧？就是不斷的歸併，最終合成一個完整的排好序的陣列。

…………………………2 2 5 6 7 8 8 9…………………………
……………………………………歸併……………………………………
…………………2 5 6 8………………2 7 8 9…………………
……………………歸併…………………………歸併……………………
……………2 6…………5 8…………2 9…………7 8……………
……………歸併…………歸併………歸併……………歸併……………
…………6……2………8……5………2……9………8……7…………

要完成上面這個程式，我們可以利用前面寫好的merge函式呢，下面是虛擬碼實現。

MERGE-SORT(A,p,r)
1  if p < r
2      q = 小於或等於(p+r)/2的最大整數
3      MERGE-SORT(A,p,q)
4      MERGE-SORT(A,q+1,r)
5      MERGE(A,p,q,r)

然後為了完成這其中q

q
的引數傳遞，將它們設定為全域性變數已經不合適了，具體的程式可以參考如下：

#include <iostream>
#include <cstdio>

using namespace std;

#define MAX_N 1000

int A[MAX_N];
int L[MAX_N/2];
int R[MAX_N/2];


void merge(int A[],int p,int q,int r);
void merge_sort(int A[],int p,int r);

int main()
{
    int n, p, q, r;
    printf("陣列長度：\n");
    cin >> n;
    printf("陣列內容：\n");
    for (int i = 0;i < n;i++)
    {
        cin >> A[i];
    }
    printf("輸入p r\n");\
        cin >> p >> r;

    merge_sort(A, p, r);

    for (int i = 0;i < n;i++)
    {
        printf("%d ", A[i]);
    }

    return 0;
}

void merge_sort(int A[],int p,int r)
{
    if(p<r)
    {
        int q=(p+r)/2;
        merge_sort(A,p,q);  
        merge_sort(A,q+1,r);
        merge(A,p,q,r);
    }
}

void merge(int A[], int p, int q, int r)
{
    int n1 = q - p + 1;
    int n2 = r - q;
    for (int i = 0;i<n1;i++)
        L[i] = A[p + i];
    for (int j = 0;j<n2;j++)
        R[j] = A[q + j + 1];
    L[n1] = 100;
    R[n2] = 100;
    for (int k = p, i = 0, j = 0;k<=r;k++)
    {
        if (L[i] <= R[j])
        {
            A[k] = L[i];
            i = i + 1;
        }
        else
        {
            A[k] = R[j];
            j = j + 1;
        }
    }
}

分析分治演算法

當我們的輸入足夠小時，比如對於某個常量c，n≤c

n \leq c
，則直接求解需要常量時間，並寫作Θ(1)
\Theta(1)
。

對於複雜的問題，我們將其分解成a

a
個子問題，每個子問題的規模是原問題的1/b
1/b
.對於這規模為n/b
n/b
的子問題，累計需要T(n/b)
T(n/b)
的時間，所以需要aT(n/b)
aT(n/b)
的時間來求解這a
a
個子問題。而這其中分解的過程也需要消耗一定的時間，記作D(n)
D(n)
，合併這些子問題也需要一定的時間，記作C(n)
C(n)
。於是又得到了一個遞迴式：

當n≤c

n \leq c
時，T(n)=Θ(1)
T(n)=\Theta(1)

其他情況時，T(n)=aT(n/b)+D(n)+C(n)

T(n)=aT(n/b)+D(n)+C(n)

下面來通過分治模式在每層遞迴時都有的三個步驟來分析歸併排序演算法，我們所考慮的是n個數的最壞情況下的執行時間。同樣的，歸併排序一個元素需要常量時間，當n>1時有如下3個步驟：

分解：分解步驟僅僅計運算元陣列的中間位置，需要常量時間，因此D(n)=Θ(1)

D(n)=\Theta(1)

解決：我們遞迴地求解兩個規模均為n/2
n/2
的子問題，將貢獻2T(n/2)
2T(n/2)
的執行時間。
合併：一個具有n個元素的子陣列上過程MERGE需要Θ(n)
\Theta(n)
的時間，所以C(n)=Θ(n)
C(n)=\Theta(n)
。

因此D(n)+C(n)

D(n)+C(n)
便等於Θ(n)
\Theta(n)
和Θ(n)
\Theta(n)
相加，可是結果依然為Θ(n)
\Theta(n)
。接著可以得到歸併排序的最壞情況執行時間的遞迴式了。

當n=1

n=1
時，T(n)=Θ(1)
T(n)=\Theta(1)

當n>1

n>1
時，T(n)=2T(n/2)+Θ(n)
T(n)=2T(n/2)+\Theta(n)

我們對上式稍作變換如下：

當n=1

n=1
時，T(n)=c
T(n)=c

當n>1

n>1
時，T(n)=2T(n/2)+cn
T(n)=2T(n/2)+cn

這個式子可以不斷的做遞迴，最後形成一個遞迴樹的。樹的第一層是cn

cn
，第二層是cn/2
cn/2
，第三層是cn/4
cn/4
，直到最後一層為c
c
。第二層有2棵子樹，第三層有4棵子樹，直到最後一程有n
n
棵子樹，因此每層的代價總共為cn
cn
。而整個樹共有lgn+1
\lg n+1
層，因此總代價為cnlgn+cn
cn\lg n+cn
。

忽略低階項和係數項，最終記為Θ(nlgn)

\Theta(n\lg n)
。

遞迴和迭代

這兩個概念也許很多童鞋依舊是老虎老鼠傻傻分不清楚，下面通過求解斐波那契數來看看它們倆的關係吧。

斐波那契數的定義：

f0=0
f_0 = 0

f1=1
f_1 = 1

fi=fi−1+fi−2(i>1)
f_i = f_{i-1}+f_{i-2} (i > 1)

遞迴：

(factorial 6)
(* 6 (factorial 5))
(* 6 (* 5 (factorial 4)))
(* 6 (* 5 (* 4 (factorial 3))))
(* 6 (* 5 (* 4 (* 3 (factorial 2)))))
(* 6 (* 5 (* 4 (* 3 (2 (factorial 1))))))
(* 6 (* 5 (* 4 (* 3 (* 2 1)))))
(* 6 (* 5 (* 4 （* 3 2))))
(* 6 (* 5 (* 4 6)))
(* 6 (* 5 24))
(* 6 120)
720

迭代：

(factorial 6)
(factorial 1 1 6)
(factorial 1 2 6)
(factorial 2 3 6)
(factorial 6 4 6)
(factorial 24 5 6)
(factorial 120 6 6)
(factorial 720 7 6)
720

遞迴的核心在於：不斷地回到起點。
迭代的核心在於：不斷地更新引數。

在下面的程式碼中：

遞迴的核心是sum的運算，sum不斷的累乘，雖然運算的數值不同，但形式和意義一樣。

而迭代的核心是product和counter的不斷更新。如上表中，product就是factorial的前2個引數不斷的累乘更新成第一個引數；而第二個引數則是counter，其不斷的加1來更新自己。

product <- counter * product 
counter <- counter + 1
#include <iostream>

using namespace std;

int factorialRecursive(int n);
int factorialIteration(int product, int counter, int max_count);

int main()
{
    int n;
    cout<<"Enter an integer:"<<endl;
    cin>>n;
    cout<<factorialRecursive(n)<<endl;
    cout<<factorialIteration(1,1,n)<<endl;

    return 0;
}

int factorialRecursive(int n)
{
    int sum=1;
    if(n==1)
        sum*=1;
    else
        sum=n*factorialRecursive(n-1);
    return sum;
}

int factorialIteration(int product, int counter, int max_count)
{
    int sum=1;
    if(counter>max_count)
        sum*=product;
    else
        factorialIteration((counter*product),(counter+1),max_count);
}
updated at 2016/09/24

// Java
    public int factorialRecursive(int n) {
        int sum = 1;
        if (n == 1) sum *= 1;
        else sum = n * factorialRecursive(n - 1);
        return sum;
    }

    public int factorialIteration(int n) {
        return factorialIterationCore(1, 1, n);
    }

    public int factorialIterationCore(int product, int counter, int maxCount) {
        if (counter > maxCount)
            return product;
        else
            return factorialIterationCore(counter * product, counter + 1, maxCount);
    }

補充問題：

關於上面的factorialIteration函式，今天收到一份郵件，我也通過再次分析學到了很多，這裡羅列一下。

第一個問題：

首先來看相對簡單的問題，該童鞋在函式內以兩種不同方式加上another_sum=2卻有著不同的結果。

int factorialIteration(int product, int counter, int max_count) {
    int sum = 1;
    int another_sum = 2;
    if(counter > max_count) {
        sum *= product;
        another_sum *= product;
    } else
        factorialIteration(counter*product, counter + 1, max_count);
}
int factorialIteration(int product, int counter, int max_count) {
    int sum = 1;
    int another_sum = 2;
    if(counter > max_count) {
        another_sum *= product;
        sum *= product;        
    } else
        factorialIteration(counter*product, counter + 1, max_count);
}

因為這個函式宣告的是int型的返回型別，但沒有用return語句，所以C++自動將其執行的最後一行語句作為了返回語句。所以這兩個函式類似於：

int factorialIteration(int product, int counter, int max_count)
{
    int sum=1;
    int another_sum=2;
    if(counter>max_count)
    {
        sum*=product;
        return another_sum*=product;
    }
    else
        factorialIteration((counter*product),(counter+1),max_count);
}


int factorialIteration(int product, int counter, int max_count)
{
    int sum=1;
    int another_sum=2;
    if(counter>max_count)
    {
        another_sum*=product;
        return sum*=product;
    }
    else
        factorialIteration((counter*product),(counter+1),max_count);
}

然而我在CodeBlocks中寫的程式碼不用return是可以的，但在Visual Studio中卻是會報錯的。

有了這個發現，我原來的程式碼也可以這樣來寫：

#include <iostream>

using namespace std;

int factorialRecursive(int n);
int factorialIteration(int product, int counter, int max_count);

int main()
{
    int n;
    cout<<"Enter an integer:"<<endl;
    cin>>n;
    cout<<factorialRecursive(n)<<endl;
    cout<<factorialIteration(1,1,n)<<endl;

    return 0;
}

int factorialRecursive(int n)
{
    int sum=1;
    if(n==1)
        sum*=1;
    else
        sum=n*factorialRecursive(n-1);
    // return sum;   // 去掉這裡的return語句
}

int factorialIteration(int product, int counter, int max_count)
{
    int sum=1;
    if(counter>max_count)
        return sum*=product;   // 在這裡加上return語句
    else
        factorialIteration((counter*product),(counter+1),max_count);
}

現在來看另一個問題：

#include <iostream>
using namespace std;

int test(int n);
int sum;

int main()
{
    cout<<test(1)<<endl;
    return 0;
}
int test(int n)
{
    sum = 1;
    sum += n;
    if (sum < 5)   
        test(n+1);
}

如果設sum為全域性變數，那麼會在test函式中每一次呼叫sum=1時都將sum重新賦值為1。整個程式最後輸出為5。這個應該沒有什麼懸念吧？

如果設sum給test內的區域性變數，則會在每一次執行int sum=1語句時都會建立一個新的sum物件，它的存放地址和之前的sum並不相同。然後整個程式最後輸出意外的是4。

#include <iostream>
using namespace std;

int test(int n);

int main()
{
    cout<<test(1)<<endl;
    return 0;
}
int test(int n)
{
    int sum = 1;
    sum += n;
    if (sum < 5)
        return test(n+1);
    // return sum;   此處有這一行程式碼命名為程式1，沒有這行程式碼命名為程式2
}

程式1的輸出是5，程式2的輸出是4。具體函式執行過程如下：

第一步，呼叫test(1)：

int sum=1
sum=2
return test(2)

第二步，呼叫test(2)：

int sum=1
sum=3
return test(3)

第三步，呼叫test(3)：

int sum=1
sum=4
return test(4)

第四步，呼叫test(4)：

int sum=1
sum=5

執行到第四步的時候，由於sum以及不比5小了，所以程式1沒有進入if語句而是執行下一句return sum，所以輸出為1。

而如果是程式2，也就是沒有return sum語句，那麼程式在執行完第四步後就會返回到第三步，最終呼叫(return) sum=4，輸出4。

第三個問題：

該童鞋還提到了尾遞迴，這裡我就來說說我的理解，如有問題歡迎大家直接評論或郵件給我。

上面程式碼中的遞迴函式factorialRecursive應該沒問題的吧。

上面的程式碼我給其命名為迭代。

int factorialIteration(int product, int counter, int max_count)
{
    int sum=1;
    if(counter>max_count)
        sum*=product;
    else
        factorialIteration((counter*product),(counter+1),max_count);
}

通過在main函式中呼叫如下程式碼來執行該函式：

cout<<factorialIteration(1,1,n)<<endl;

當然，也可以另外寫一個函式如下：

int factorialIter(int n)
{
    return factorialIteration(1,1,n);
}

並通過在main函式中直接呼叫該函式來做計算：

cout<<factorialIter(n)<<endl;

函式factorialIteration中的max_count我們稱其為“迴圈不變數”，也就是對於整個運算過程而言這個變數是不變的。為了讓大家更加印象深刻，將前面出現過的東西再來複制一遍：

(factorial 6)
(factorial 1 1 6)
(factorial 1 2 6)
(factorial 2 3 6)
(factorial 6 4 6)
(factorial 24 5 6)
(factorial 120 6 6)
(factorial 720 7 6)
720

從第二行開始的factorial的第三個引數”6“就是迴圈不變數。

尾遞迴：

在電腦科學中，尾呼叫是一個作為過程最後一步的子例程呼叫執行。如果尾呼叫可能在以後的呼叫鏈中再呼叫這同一個子例程，那麼這個子例程就被稱為是尾遞迴，它是遞迴的一個特殊情況。尾遞迴非常有用，在實現中也容易處理。尾呼叫可以不通過在呼叫堆疊中新增新的棧幀而實現。

傳統上，尾部呼叫消除是可選的。然而，在函數語言程式設計語言中，尾呼叫消除往往由語言標準作為保障，這種保證允許使用遞迴，在特定情況下的尾遞迴，來代替迴圈。在這種情況下，儘管用它作為一種優化是不正確的（儘管它可能是習慣用法）。在尾遞迴中，當一個函式呼叫它自身這種特殊情況下，可能呼叫消除比傳統的尾呼叫更加合適。

迭代：

迭代是一個重複過程，它的目的是接近既定的目標或結果。每次重複的過程也稱為”迭代“，作為迭代的結果都將作為下一次迭代的起點。

迭代在計算中是指的計算機程式中的重複的語句塊。它可以表示兩個專業術語，同義重複，以及描述一種具有可變狀態重複的具體形式。然後令人費解的是，它也可以表示通過顯式重複結構的任何重複，而不管其可變性。

在第一個意義上，遞迴是迭代的一個例子，但通常用”遞迴“來標記，而不作為”迭代“的例子。

在第二個意義上，（更加狹義地）迭代描述了一種程式設計風格。這與一個有著更有宣告性方法的遞迴有著鮮明的對比。

第三個意義上，使用while或for迴圈，以及使用map或fold的函式也被視為迭代。

（以上定義部分摘自英文維基百科）

關於遞迴和尾遞迴在函數語言程式設計中的應用也可以看這裡：【Scheme歸納】3 比較do, let, loop

感謝您的訪問，希望對您有所幫助。 歡迎大家關注、收藏以及評論。

為使本文得到斧正和提問，轉載請註明出處：
http://blog.csdn.net/nomasp

相關文章