【資料結構】回顧優先佇列（堆）

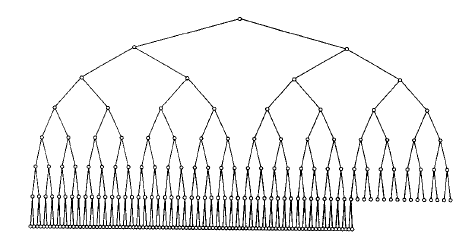
1.優先佇列有兩項基本操作：插入（insert）和刪除最小項（deleteMin），後者的工作是找出、返回和刪除優先佇列中最小的元素。而insert操作則等價於enqueue（入隊），deleteMin則等價於dequeue（出隊）。補充：C++提供2個版本的deleteMin，一個刪除最小項，另一個在刪除最小項的同時在通過引用傳遞的物件中儲存所刪除的值。

2.優先佇列的類介面

template <typename Comparable>
class BinaryHeap
{
public:
    explicit BinaryHeap(int capacity=100);
    explicit BinaryHeap(const vector<Comparable> & items);

    bool isEmpty() const;
    const Comparable & findMin() const;

    void insert(const Comparable & x);
    void deleleMin();
    void deleteMin(Comparable & minItem);
    void makeEmpty();

private:
    int currentSize;
    vector<Comparable> array;
    void buildHeap();
    void percolateDown(int hole);
};

3.插入到一個二叉堆

void insert(const Comparable & x)
{
    if(currentSize==array.size()-1)
        array.resize(array.size()*2);

    int hole=++currentSize;
    for(;hole>1&&x<array[hole/2];hole/=2)
        array[hole] =array[hole/2];
    array[hole]=x;
}

4.在二叉堆中執行deleteMin

void deleteMin()
{
    if(isEmpty())
        throw UnderflowException();

    array[1]=array[currentSize--];
    percolateDown(1);
}

void deleteMin(Comparable & minItem)
{
    if(isEmpty())
        throw UnderflowException();

    minItem=array[1];
    arrary[1]=array[currentSize--];
    percolateDown(1);
}

void percolateDown(int hole)
{
    int child;
    Comparable tmp=array[hole];

    for(;hole*2<=currentSize;hole=child)
    {
        child=hole*2;
        if(child!=currentSize&&array[child+1]<array[child])
            child++;
        if(array[child]<tmp)
            array[hole]=array[child];
        else 
            break;
    }
    array[hole]=tmp;
}

5.左式堆（leftist heap）像二叉堆那樣既有結構性質，又有堆序性質。左序堆也是二叉樹，它和二叉樹的唯一區別是：左式堆不是理想平衡的（perfectly balanced），而且事實上是趨於非常不平衡的。左式堆的性質：對於堆中的每一個結點X，左兒子的零路徑至少於右兒子的零路徑長一樣大。由於左式堆是趨向於加深左路徑，因此右路徑應該很短，沿左式堆右側的右路徑確實是該堆中最短的路徑。否則就會存在一條路徑通過某個結點X並取得左兒子，此時X就破壞了左式堆的性質。

6.對左式堆的基本操作是合併（插入只是合併的特殊情形）。左式堆型別宣告：

template <typename Comparable>
class LeftistHeap
{
public:
    LeftistHeap();
    LeftistHeap(const LeftistHeap & rhs);
    ~LeftistHeap();

    bool isEmpty() const;
    const Comparable & findMin() const;

    void insert(const Comparable & x);
    void deleteMin();
    void deleteMin(Comparable & minItem);
    void makeEmpty();
    void merge(LeftistHeap & rhs);

    const LeftistHeap & operator=(const LeftistHeap & rhs);

private:
    struct LeftistNode
    {
        Comparable element;
        LeftistNode *left;
        LeftistNode *right;
        int npl;

        LeftistNode(const Comparable & theElement, LeftistNode * lt=NULL,
                    LeftistNode * rt=NULL,int np=0)
            :element(theElement),left(lt),right(rt),npl(np){}
    };

    LeftistNode *root;

    LeftistNode *merge (LeftistNode *h1,LeftistNode *h2);
    LeftistNode *merge1(LeftistNode *h1,LeftistNode *h2);

    void swapChildren(LeftistNode *t);
    void reclainMemory(LeftistNode *t);
    LeftistNode *clone(LeftistNode *t) const;
};

7.合併左式堆的驅動程式和實際程式

void merge(LeftistHeap & rhs)
{
    if(this==&rhs)
        return;

    root=merge(root,rhs.root);
    rhs.root=NULL;
}

LeftistNode * merge(LeftistNode *h1,LeftistNode *h2)
{
    if(h1==NULL)
        return h2;
    if(h2==NULL)
        return h1;
    if(h1->element<h2->element)
        return merge1(h1,h2);
    else 
        return merge1(h2,h1);
}

LeftistNode *merge1(LeftistNode *h1,LeftistNode *h2)
{
    if(h1->left==NULL)
        h1->left=h2;
    else
    {
        h1->right=merge(h1->right,h2);
        if(h1->left->npl<h1->right-np1)
            swapChildren(h1);
        h1->npl=h1->right->npl+1;
    }
    return h1;
}

8.左式堆的insert程式和deleteMin程式

void insert(const Comparable & x)
{
    root=merge(new LeftistNode(x).root);
}

void deleteMin()
{
    if(isEmpty())
        throw UnderflowException();

    LeftistNode *oldRoot=root;
    root=merge(root->left,root->right);
    delete oldRoot;
}

void delteMin(Comparable & minItem)
{
    minItem=findMin();
    deleteMin();
}

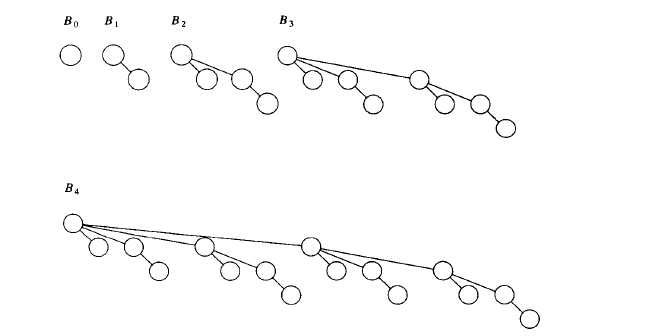
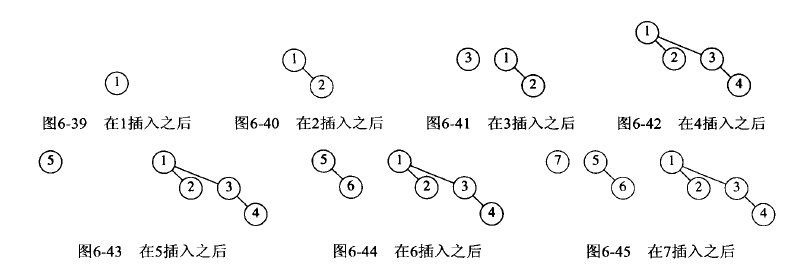
9.二項佇列不是一棵堆序的樹，而是堆序的集合，稱為森林（forest）。

10.二項佇列類構架及結點定義：

template <typename Comparable>
class BinomialQueue
{
public:
    BinomialQueue();
    BinomialQueue(const Comparable & item);
    BinomialQueue(const BinomialQueue & rhs);
    ~BinomialQueue();

    bool isEmpty() const;
    const Comparable &  findMin() const;

    void insert(const Comparable & x);
    void deleteMin();
    void deleteMin(Comparable & minItem);

    void makeEmpty();
    void merge(BinomialQueue & rhs);

    const BinomialQueue & operator = (const BinomialQueue & rhs);

private:
    struct BinomialNode
    {
        Comparable element;
        BinomialNode *leftChild;
        BinomialNode *nextSibling;

        BinomialNode(const Comparable & theElement,
                     BinomialNode *lt,BinomialNode *rt)
            :element(theElement).leftchild(lt).nextSiblig(rt){}
    };

    enum {DEFAULT_TREES=1};

    int currentSize;
    vector<BinomialNode*> theTrees;

    int findMinIndex() const;
    int capacity() const;
    BinomialNode * combineTrees(BinomialNode *t1,BinomialNode *t2);
    void makeEmpty(BinomialNode * & t);
    BinomialNode * clone(BinomialNode * t) const;
};

11.在STL中，二叉堆是通過稱為priority_queue的類别範本實現的，該類别範本可以在標準標頭檔案queue中找到。STL 實現了一個最大堆而不是最小堆，因此所訪問的項就是最大的項而不是最小的項。其鍵成員函式如下：

void push(const Object & x);
const Object & top() const;
void pop();
bool empty();
void clear();

---

---

感謝您的訪問，希望對您有所幫助。

歡迎大家關注或收藏、評論或點贊。

---

為使本文得到斧正和提問，轉載請註明出處：
http://blog.csdn.net/nomasp

---