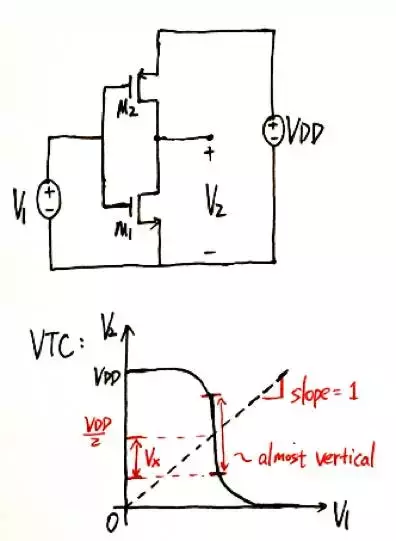
在上一講(震驚!UCLA電路大佬用的MOS模型竟然不是平方律而是...)中我們給大家介紹了EKV模型的基本概念以及在大訊號和小訊號分析中的應用。尤其在大訊號分析中,EKV圖形化的方法簡單直觀,有著得天獨厚的優勢。在進入MOSFET不同反型區的推導前,我們首先講兩個例子,教大家如何用EKV模型秒掉拉扎維(的類比電路面試考題),同時也讓大家再次領略EKV模型的威力。
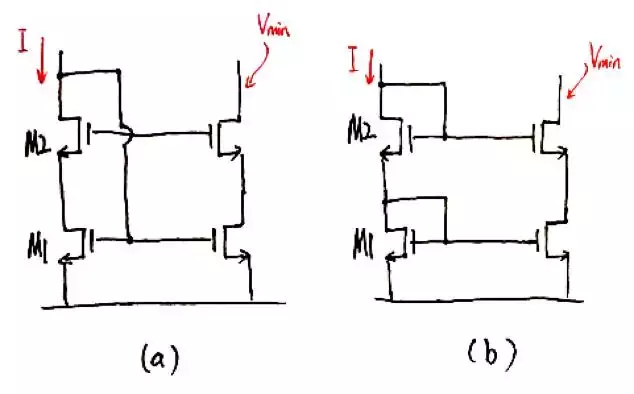
上圖所示是兩個電流鏡電路。對於一個電流鏡電路,高輸出電阻和高電壓裕度(voltageheadroom)是兩個重要的指標。由於共源共柵管的存在,兩個電路的輸出電阻都很大。那麼哪個電路的電壓裕度更大呢?我們還是透過畫三角形的方式來分析。
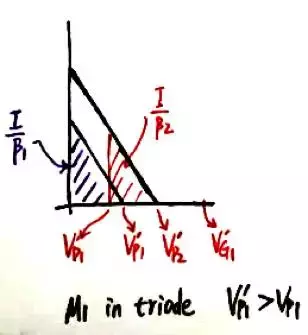
對於(a),為了簡化分析,假設M1和M2有相同的(W/L),因而β相同。在下圖中的偏置電壓下(M2的偏置電路在電路圖中未畫出),M1和M2都處在飽和狀態,由於流過的電路以及β都相同,所以兩個三角形的面積相同。外電路的最小電壓Vmin=Vp2。
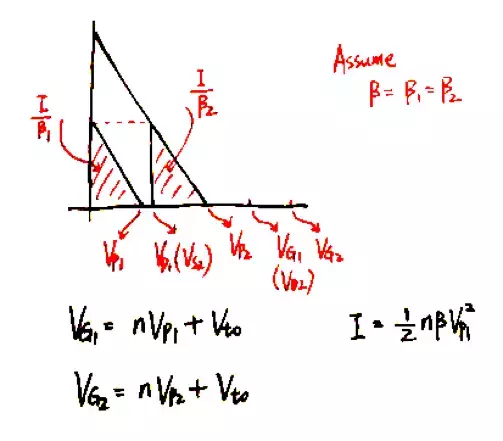
如果逐漸減小M2的偏置電壓VG2,右側的小三角形會隨之左移,直至VS2恰好等於VP1,此時為臨界偏置點,此時電路有最大的電壓裕度:
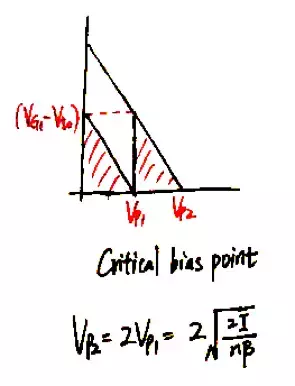
如果繼續減小VG2,M1將進入三極體區。由於輸入電流恆定,因而代表M1電流的紫色梯形面積和之前的三角形面積相等,所以Vp1會自動增大。
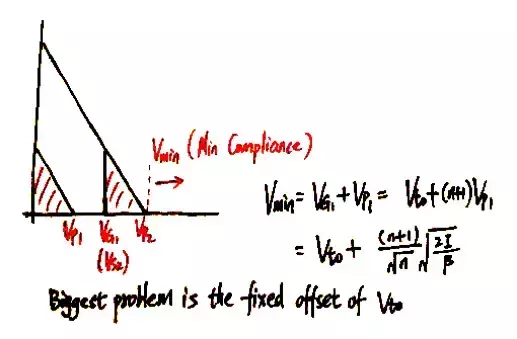
接下來我們分析(b)中的電路,由於VG1=Vs2,從圖中可知,Vmin比(a)中的電路大約多出了一個閾值電壓的大小。
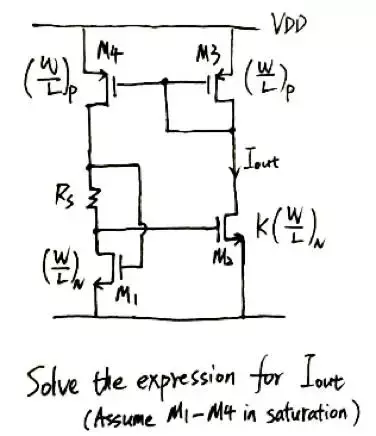
第二個例子我們嘗試用EKV模型來求解拉扎維模電書上的一道習題(第11章習題第一題),題目如下圖所示:
我們先後畫出左右兩條支路的“三角形”示意圖,PMOS電流鏡的兩個MOS管對應的三角形完全相同,而左邊支路的NMOS對應的三角形面積是右邊NMOS的K倍,因而左邊三角形邊長是右邊的根號K倍。由此可以輕鬆地計算出輸出電流的表示式。
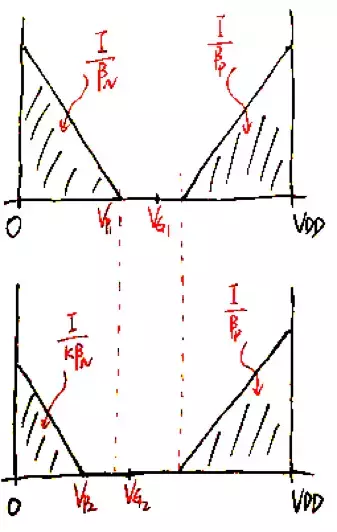
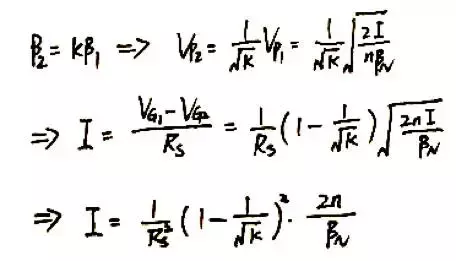
對比拉扎維書的解答,唯一的不同是這裡還考慮了體效應因子n(所以如果拉扎維的標準答案是100分使用EKV方法求解的答案應該得120分:))。
反型區模型
在上一講中我們提到,EKV模型在強反型區(stronginversion)、中間反型區(moderateinversion)和弱反型區(weakinversion)連續準確。強反型區自然就是大家熟悉的平方率模型,也就是之前反覆使用的“三角形”(左圖);但實際上,在Vp附近的轉折不是突變而是連續的(右圖)。
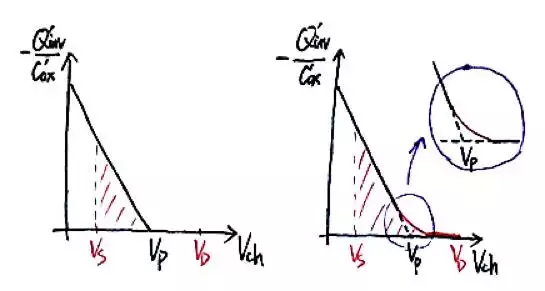
首先我們來簡單學習一下弱反型區的模型。MOS管在弱反型區的工作狀態和BJT基本相同,擴散電流(diffusioncurrent)佔主導,電流和電壓之間呈指數關係。

由最後推出的電流公式可知,當VDS大於約5倍的VT時,電流就基本飽和,I-V特性曲線如下圖所示:
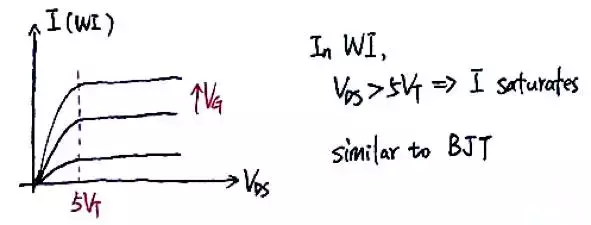
有了強弱反型區的模型之後,中間反型區的模型可以透過插值公式得到。可以驗證,這個公式在強弱反型區均適用。

短溝道效應
講完了MOS管在不同反型區的模型,接下來我們就談一談兩個短溝道效應——溝道長度調製效應和速度飽和效應。
(1)溝道長度調製效應
溝道長度調製效應可以說是類比電路設計中最重要的效應之一,它決定了一個MOS管的輸出電阻。如下圖所示,在一個MOS管的溝道中,從漏端(D)到源端(S)溝道電壓連續下降。如果MOS管處於飽和狀態,那麼溝道中存在夾斷點,該點的溝道電壓即為夾斷電壓(pinch-offvoltage)。夾斷點和漏端之間為耗盡區,和源端之間有載流子,這段長度稱為有效溝道長度Leff。增大漏端電壓VD,夾斷點會左移,Leff也會隨之減小。
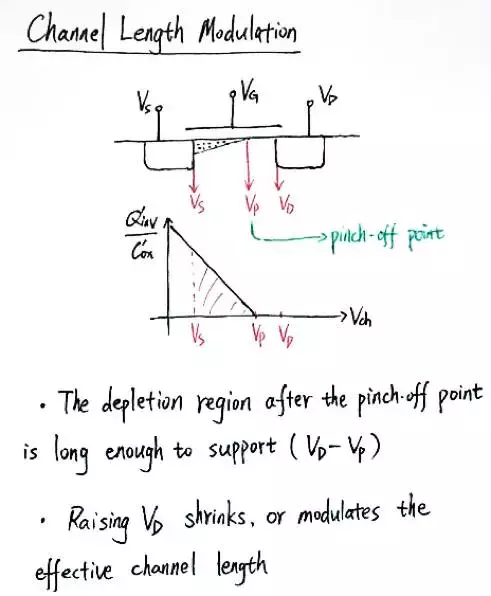
經過推導,我們可以看到MOS管的輸出電導go=I/VA=I/(VE*L),通常情況下,VE可以看做一個常數,因而MOS管的輸出電阻和溝道長度L成正比,和偏置電路I成反比。

(2)速度飽和效應
我們知道,MOS管溝道的橫向電場E= VDS/L,當電場強度較小時,載流子的漂移速度(driftvelocity)v= μ*E,但當漂移速度和電子的熱運動速度相近時,這種線性關係就不再成立,漂移速度會趨於飽和。
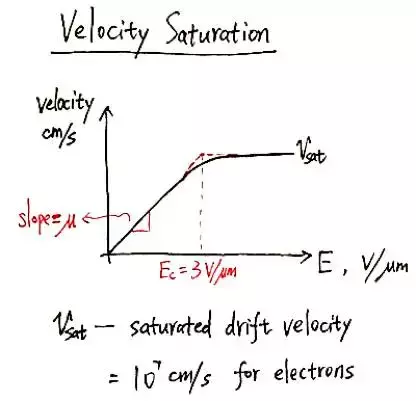
下圖中的插值公式同時適用於飽和區和速度飽和區:
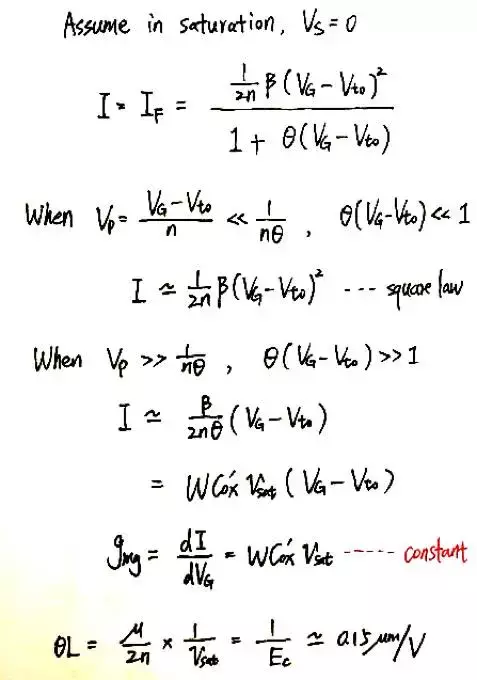

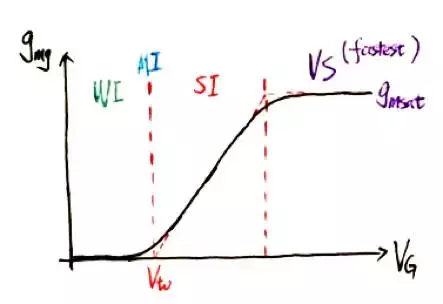
我們來對講過的內容做一個小小的總結,下圖涵蓋了MOS管從弱反型區到強反型區再到速度飽和區中gmg的值。在速度飽和區,跨導為一個常數,不再隨柵極電壓變化。
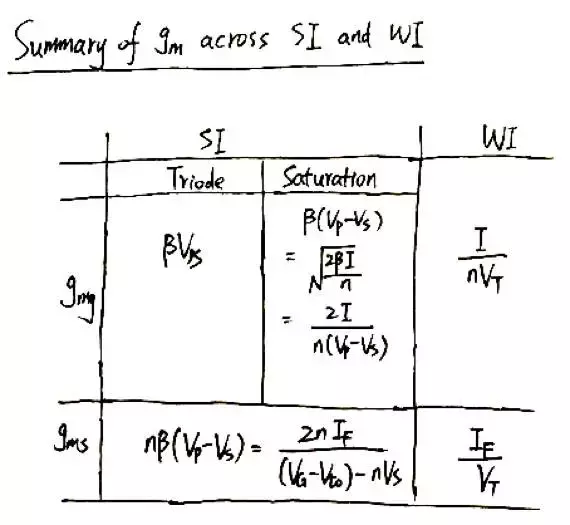
在強反型區和弱反型區的跨導表示式如下表:
在設計中我們通常還會關注一個重要的指標——跨導效率(transconductanceefficiency),即跨導與電流的比值:
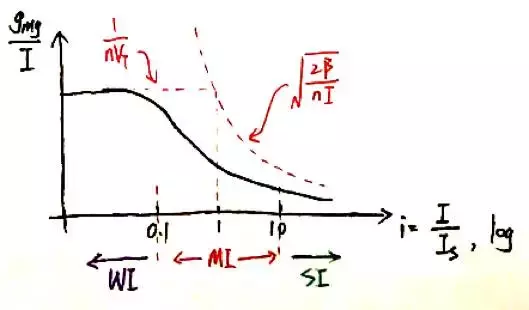
跨導決定了放大器頻寬,而跨導效率則決定了達到該頻寬需要多少電流。看起來跨導效率是弱反型最好,因此現在許多低功耗設計會把MOSFET偏置在靠近弱反區的地方。然而,在弱反區的噪聲,失調(offset)以及大訊號效能需要仔細設計,這也是弱反型設計帶來的挑戰。
最後給大家留一個簡單的練習題: