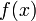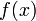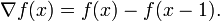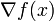影象處理中的一些基本問題解釋

出處：http://www.cnblogs.com/gnuhpc/

 轉自：http://www.cnblogs.com/gnuhpc/archive/2012/10/13/2722879.html

1.邊緣檢測：

邊緣檢測是影象處理和計算機視覺中的基本問題，邊緣檢測的目的是標識數字影象中亮度變化明顯的點。影象屬性中的顯著變化通常反映了屬性的重要事件和變化。這些包括（i）深度上的不連續、（ii）表面方向不連續、（iii）物質屬性變化和（iv）場景照明變化。邊緣檢測是影象處理和計算機視覺中，尤其是特徵提取中的一個。

影象邊緣檢測大幅度地減少了資料量，並且剔除了可以認為不相關的資訊，保留了影象重要的結構屬性。有許多方法用於邊緣檢測，它們的絕大部分可以劃分為兩類：基於查詢的一類和基於零穿越的一類。基於查詢的方法通過尋找影象一階導數中的最大和最小值來檢測邊界，通常是將邊界定位在梯度最大的方向（想想一階導數的含義是影象變化的速度，最大的自然就是變化最大的了）。基於零穿越的方法通過尋找影象二階導數零穿越來尋找邊界，通常是Laplacian過零點或者非線性差分表示的過零點。

2.差分

差分，又名差分函式或差分運算，是數學中的一個概念。它將原函式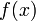對映到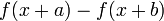。差分運算，相應於微分運算，是微積分中重要的一個概念。差分的定義分為前向差分和逆向差分兩種。

前向差分

函式的前向差分通常簡稱為函式的差分。對於函式，如果：

，

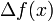則稱為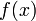的一階前向差分。在微積分學中的有限差分（finite differences），前向差分通常是微分在離散的函式中的等效運算。差分方程的解法也與微分方程的解法相似。當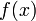是多項式時，前向差分為Delta運算元，一種線性運算元。前向差分會將多項式階數降低1。

逆向差分

對於函式，如果：

則稱為的一階逆向差分。

3.索貝爾運算元

索貝爾運算元（Sobel operator）是影象處理中的運算元之一，主要用作邊緣檢測。在技術上，它是一離散性差分運算元，用來運算影象亮度函式的梯度之近似值。在影象的任何一點使用此運算元，將會產生對應的梯度向量或是其法向量。

公式

該運算元包含兩組3x3的矩陣，分別為橫向及縱向，將之與影象作平面卷積，即可分別得出橫向及縱向的亮度差分近似值。如果以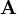代表原始影象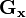，及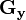分別代表經橫向及縱向邊緣檢測的影象，其公式如下:

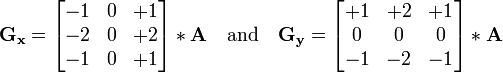
影象的每一個畫素的橫向及縱向梯度近似值可用以下的公式結合，來計算梯度的大小。

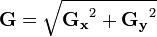
然後可用以下公式計算梯度方向。

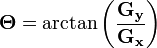
在以上例子中，如果以上的角度Θ等於零，即代表影象該處擁有縱向邊緣，左方較右方暗。

4.矩陣卷積

函式矩陣的卷積

定義兩個函式矩陣的卷積可以用類似於兩個矩陣乘法的運算規則，即將兩個元素相乘的符號都用卷積來替換，譬如

5.影象梯度
感性認識：梯度值就是影象灰度值的顯著變化的地方。不同的運算元對應了不同的求梯度的方法：
以Sobel運算元（效果較好）為例：
對於數字影象，可以用一階差分代替一階微分；

　　△xf(x,y)=f(x,y)-f(x-1,y);

　　△yf(x,y)=f(x,y)-f(x,y-1)

求梯度時對於平方和運算及開方運算，可以用兩個分量的絕對值之和表示，即：

　　G[f(x,y)]={[△xf(x,y)] +[△yf(x,y)] } |△xf(x,y)|+|△yf(x,y)|;

　　Sobel梯度運算元是先做成加權平均，再微分，然後求梯度，即：

　　△xf(x,y)= f(x-1,y+1) + 2f(x,y+1) + f(x+1,y+1)- f(x-1,y-1) - 2f(x,y-1) - f(x+1,y-1);

　　△yf(x,y)= f(x-1,y-1) + 2f(x-1,y) + f(x-1,y+1)- f(x+1,y-1) - 2f(x+1,y) - f(x+1,y+1);

　　G[f(x,y)]=|△xf(x,y)|+|△yf(x,y)|;

6.高斯金字塔
　對於大小為w×i的影象I，高斯金字塔Gj由I的幾個解析度減小的高斯影象Ii(i是下標,下同)組成，其中，i={0,1,...,j}代表金字塔的級數.影象Ii 的大小為(w/2i)×(h/2i).[2i表示2的i次方]。影象Ii是通過對影象Ii-1(i-1是下標)進行隔行隔列取樣而得到的圖。

作者：gnuhpc
出處：http://www.cnblogs.com/gnuhpc/