Codeforces Round #217前三題

果7發表於2013-12-19
A. Rook, Bishop and King
time limit per test
1 second
memory limit per test
256 megabytes
input
standard input
output
standard output

Little Petya is learning to play chess. He has already learned how to move a king, a rook and a bishop. Let us remind you the rules of moving chess pieces. A chessboard is 64 square fields organized into an 8 × 8 table. A field is represented by a pair of integers (r, c)— the number of the row and the number of the column (in a classical game the columns are traditionally indexed by letters). Each chess piece takes up exactly one field. To make a move is to move a chess piece, the pieces move by the following rules:

  • A rook moves any number of fields horizontally or vertically.
  • A bishop moves any number of fields diagonally.
  • A king moves one field in any direction — horizontally, vertically or diagonally.

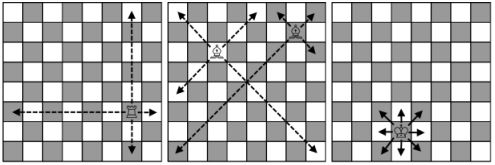The pieces move like that

Petya is thinking about the following problem: what minimum number of moves is needed for each of these pieces to move from field(r1, c1) to field (r2, c2)? At that, we assume that there are no more pieces besides this one on the board. Help him solve this problem.

Input

The input contains four integers r1, c1, r2, c2 (1 ≤ r1, c1, r2, c2 ≤ 8) — the coordinates of the starting and the final field. The starting field doesn't coincide with the final one.

You can assume that the chessboard rows are numbered from top to bottom 1 through 8, and the columns are numbered from left to right 1 through 8.

Output

Print three space-separated integers: the minimum number of moves the rook, the bishop and the king (in this order) is needed to move from field (r1, c1) to field (r2, c2). If a piece cannot make such a move, print a 0 instead of the corresponding number.

Sample test(s)
input
4 3 1 6
output
2 1 3
input
5 5 5 6
output
1 0 1

題目大意：從一個點到另一個點，經過三種變換，問分別用每種變換可以到的最小步數。第一種是橫著豎著走，答案直接分為1，2即可。第二種斜著走，答案分為1 2 0三種，0表示到達不了，畫一個方格走一下就懂了。坑在了第三種前面兩種每次走的路程任意，而第三種每次只能走一步，可以斜著橫著豎著走。竟然沒心沒肺的寫了個bfs......直接比較橫縱座標差值，誰大就可以了。。這個題目和昨天晚上打的cf題目很相似，不過昨天晚上那個需要判斷越界。


題目地址：A. Rook, Bishop and King


AC程式碼：

#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
int a,b,c,d;
int visi[10][10];
int res[10][10];
int dir[8][2]={{-1,0},{1,0},{0,1},{0,-1},{-1,1},{-1,-1},{1,1},{1,-1}};

void bfs()
{
    queue<int> mq;
    mq.push(a*10+b);
    //cout<<a<<" "<<b<<"dsd"<<endl;
    memset(visi,0,sizeof(visi));
    visi[a][b]=1;
    memset(res,0,sizeof(res));

    while(!mq.empty())
    {
        int cur=mq.front();
        mq.pop();
        int tx,ty;
        tx=cur/10,ty=cur%10;
        //cout<<tx<<" "<<ty<<endl;

        if(tx==c&&ty==d)
        {
            //cout<<"dsa"<<endl;
            return;
        }
        int cx,cy;
        for(int i=0;i<8;i++)
        {
            cx=tx+dir[i][0],cy=ty+dir[i][1];
            if(cx>=1&&cx<=8&&cy>=1&&cy<=8&&!visi[cx][cy])
            {
                res[cx][cy]=res[tx][ty]+1;
                visi[cx][cy]=1;
                mq.push(cx*10+cy);
            }
        }
   }
}

int main()
{
    int s1,s2;
    while(cin>>a>>b>>c>>d)
    {
        if(a==c||b==d)
            s1=1;
        else
            s1=2;

        if(a+b==c+d||a+d==b+c)
            s2=1;
        else if(abs(a+b-c-d)%2==0)
            s2=2;
        else
            s2=0;
        bfs();
        printf("%d %d %d\n",s1,s2,res[c][d]);
    }
    return 0;
}



B. Berland Bingo
time limit per test
1 second
memory limit per test
256 megabytes
input
standard input
output
standard output

Lately, a national version of a bingo game has become very popular in Berland. There are n players playing the game, each player has a card with numbers. The numbers on each card are distinct, but distinct cards can have equal numbers. The card of the i-th player contains mi numbers.

During the game the host takes numbered balls one by one from a bag. He reads the number aloud in a high and clear voice and then puts the ball away. All participants cross out the number if it occurs on their cards. The person who crosses out all numbers from his card first, wins. If multiple people cross out all numbers from their cards at the same time, there are no winners in the game. At the beginning of the game the bag contains 100 balls numbered 1 through 100, the numbers of all balls are distinct.

You are given the cards for each player. Write a program that determines whether a player can win the game at the most favorable for him scenario or not.

Input

The first line of the input contains integer n (1 ≤ n ≤ 100) — the number of the players. Then follow n lines, each line describes a player's card. The line that describes a card starts from integer mi (1 ≤ mi ≤ 100) that shows how many numbers the i-th player's card has. Then follows a sequence of integers ai, 1, ai, 2, ..., ai, mi (1 ≤ ai, k ≤ 100) — the numbers on the i-th player's card. The numbers in the lines are separated by single spaces.

It is guaranteed that all the numbers on each card are distinct.

Output

Print n lines, the i-th line must contain word "YES" (without the quotes), if the i-th player can win, and "NO" (without the quotes) otherwise.

Sample test(s)
input
3
1 1
3 2 4 1
2 10 11
output
YES
NO
YES
input
2
1 1
1 1
output
NO
NO


題目大意：每次有n個人，每個人手上拿了若干卡片，每個卡片編號不一樣，當然同一個人手裡的編號不會重複。然後一個人在點號，他報到哪一個號，持有相應卡片的人就把那張卡片劃掉，最先被劃掉所有卡片的人會得到獎勵，問誰有可能獲得獎勵，如果可能輸出yes，否則輸出no。


解題思路：可以直接判斷集合包含子集的問題，每個人是一個集合，集合裡的元素就是自己的卡片，可以包含別人的集合，那麼你就是no。


題目地址：A. Rook, Bishop and King


AC程式碼：

#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;

int a[102];
int visi[102][102];
int t[102];
int n;

int cal(int a,int b)
{
    int i;
    for(i=1;i<=100;i++)
    {
        if(!visi[a][i]&&visi[b][i]) return 0;
    }
    return 1;
}

void solve()
{
    int i,j;
    for(i=1;i<=n;i++)
    {
        for(j=1;j<=n;j++)
        {
            if(i==j) continue;
            if(cal(i,j))
                t[i]=0;
        }
    }
}

int main()
{
    int d,i,x,j;
    while(cin>>n)
    {
        memset(visi,0,sizeof(visi));
        for(i=1;i<=n;i++)
        {
            scanf("%d",&d);
            for(j=1;j<=d;j++)
            {
                scanf("%d",&x);
                visi[i][x]=1;
            }
        }

        for(i=1;i<=n;i++)
            t[i]=1;
        solve();

        for(i=1;i<=n;i++)
        {
            if(t[i]==1)
                puts("YES");
            else
                puts("NO");
        }
    }
    return 0;
}


C. Mittens
time limit per test
1 second
memory limit per test
256 megabytes
input
standard input
output
standard output

A Christmas party in city S. had n children. All children came in mittens. The mittens can be of different colors, but each child had the left and the right mitten of the same color. Let's say that the colors of the mittens are numbered with integers from 1 to m, and the children are numbered from 1 to n. Then the i-th child has both mittens of color ci.

The Party had Santa Claus ('Father Frost' in Russian), his granddaughter Snow Girl, the children danced around the richly decorated Christmas tree. In fact, everything was so bright and diverse that the children wanted to wear mittens of distinct colors. The children decided to swap the mittens so that each of them got one left and one right mitten in the end, and these two mittens were of distinct colors. All mittens are of the same size and fit all the children.

The children started exchanging the mittens haphazardly, but they couldn't reach the situation when each child has a pair of mittens of distinct colors. Vasily Petrov, the dad of one of the children, noted that in the general case the children's idea may turn out impossible. Besides, he is a mathematician and he came up with such scheme of distributing mittens that the number of children that have distinct-colored mittens was maximum. You task is to repeat his discovery. Note that the left and right mittens are different: each child must end up with one left and one right mitten.

Input

The first line contains two integers n and m — the number of the children and the number of possible mitten colors (1 ≤ n ≤ 5000, 1 ≤ m ≤ 100). The second line contains n integers c1, c2, ... cn, where ci is the color of the mittens of the i-th child (1 ≤ ci ≤ m).

Output

In the first line, print the maximum number of children who can end up with a distinct-colored pair of mittens. In the next n lines print the way the mittens can be distributed in this case. On the i-th of these lines print two space-separated integers: the color of the left and the color of the right mitten the i-th child will get. If there are multiple solutions, you can print any of them.

Sample test(s)
input
6 3
1 3 2 2 1 1
output
6
2 1
1 2
2 1
1 3
1 2
3 1
input
4 2
1 2 1 1
output
2
1 2
1 1
2 1
1 1


題目大意：襪子配套，要求儘量多的襪子配對了以後品種不一樣。


 解題思路：自己思路是正確的，開始還以為自己哪裡想錯了呢，我覺得就是貪心的思想，先排個序，把小號先放一下，不過左右支要標號，然後再放大號的，詳解見程式碼。


  題目地址：C. Mittens


AC程式碼：

#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;

int a[105];
int p[5002][2];

int main()
{
    int n,m,i,d;
    while(cin>>n>>m)
    {
        memset(a,0,sizeof(a));
        memset(p,0,sizeof(p));
        for(i=1;i<=n;i++)
        {
            scanf("%d",&d);
            a[d]+=2;      //先把各種類的統計出來
        }

        int t=1;
        int x=0;
        while(1)      //先放小號的
        {
            if(t==n+1) break;
            for(i=1;i<=m;i++)
            {
                if(a[i]>0)
                {
                    a[i]--;
                    p[t++][x]=i;
                    if(x==0) x=1;
                    else x=0;
                    break;
                }
            }
        }

        x=1;
        int flag=0;
        t=1;
        while(1)     //再放大號的
        {
            if(t==n+1) break;
            for(i=1;i<=n;i++)
            {
                if(a[i]>0)
                {
                    a[i]--;
                    p[t++][x]=i;
                    if(x==0) x=1;
                    else x=0;
                    break;
                }
            }
        }

        int ans=0;
        for(i=1;i<=n;i++)
        {
            if(p[i][0]!=p[i][1])
                ans++;
        }

        cout<<ans<<endl;
        for(i=1;i<=n;i++)
        {
            printf("%d %d\n",p[i][0],p[i][1]);
        }
    }
    return 0;
}

/*
5 3
1 1 2 2 3
10 3
1 1 1 2 2 2 2 2 2 3
*/


相關文章