HDU 4720Naive and Silly Muggles熱身賽2 1005題(分銳角鈍角三角形討論)

果7發表於2013-09-11
AI

Naive and Silly Muggles

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 152    Accepted Submission(s): 107


Problem Description
Three wizards are doing a experiment. To avoid from bothering, a special magic is set around them. The magic forms a circle, which covers those three wizards, in other words, all of them are inside or on the border of the circle. And due to save the magic power, circle's area should as smaller as it could be.
Naive and silly "muggles"(who have no talents in magic) should absolutely not get into the circle, nor even on its border, or they will be in danger.
Given the position of a muggle, is he safe, or in serious danger?
 

Input
The first line has a number T (T <= 10) , indicating the number of test cases.
For each test case there are four lines. Three lines come each with two integers xi and yi (|xi, yi| <= 10), indicating the three wizards' positions. Then a single line with two numbers qx and qy (|qx, qy| <= 10), indicating the muggle's position.
 

Output
For test case X, output "Case #X: " first, then output "Danger" or "Safe".
 

Sample Input
3
0 0
2 0
1 2
1 -0.5

0 0
2 0
1 2
1 -0.6

0 0
3 0
1 1
1 -1.5





 



Sample Output




Case #1: Danger
Case #2: Safe
Case #3: Safe





 



Source



2013 ACM/ICPC Asia
 Regional Online —— Warmup2



 








題目大意：給你三個點，找一個最小的圓能把三個點包住。點可以允許在圓內。再給你另一個點，如果該點在圓內或圓上輸出Danger，在圓外輸出Safe。開始寫的是直接算外接圓，這樣三個點都在圓上，第三組資料過不了。看了下博博的程式碼，沒想到直接算重心？正在想為什麼的時候，就聽到吉吉說是資料水了。。我們求外接圓的話對銳角三角形是可以的，但是如果是鈍角三角形的話。可以把圓適當的往鈍角所對的邊中點移動，那樣半徑會變小。因為題目說了點可以在圓內或者圓上。








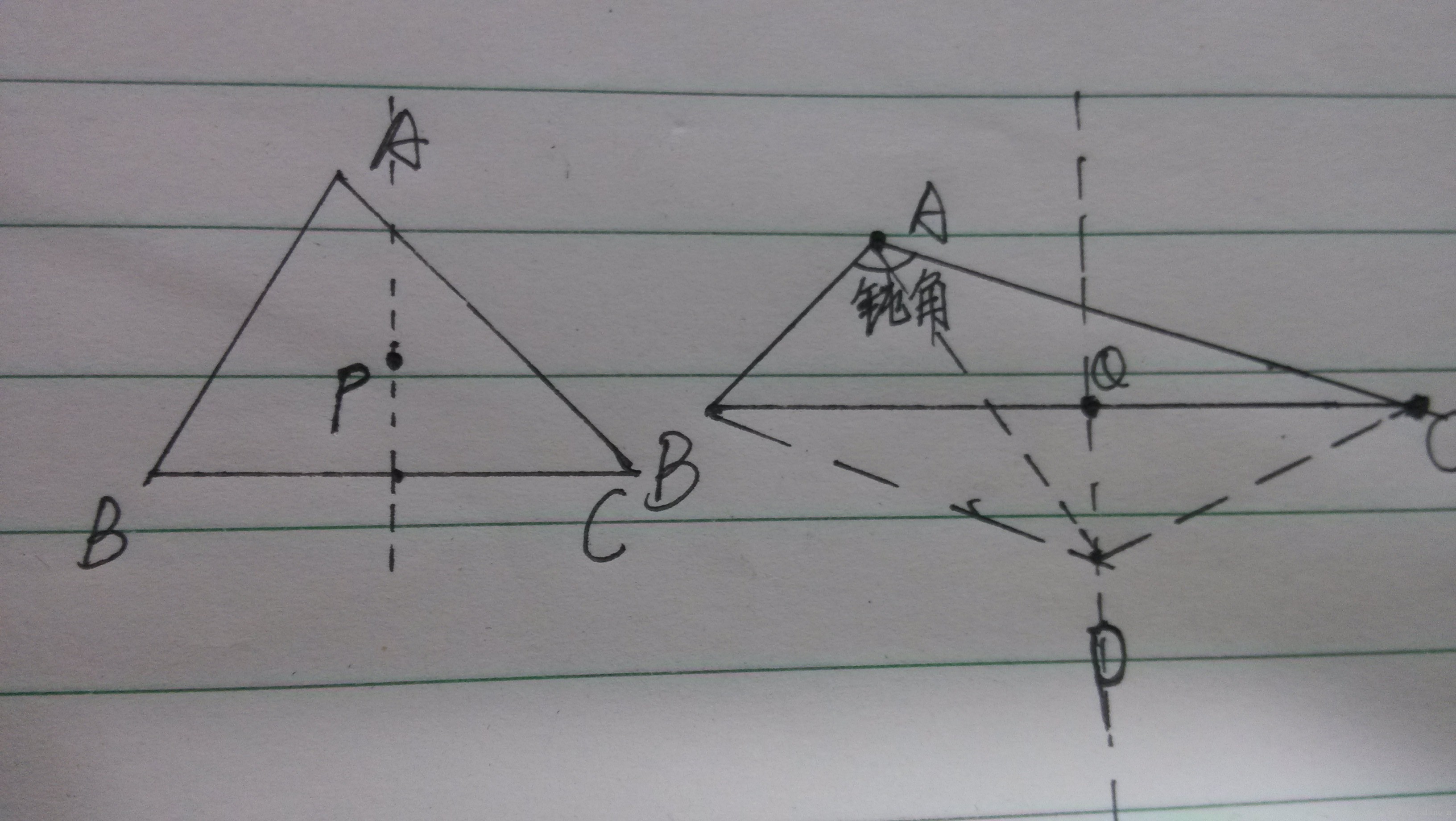
如圖，如果是銳角三角形，外心肯定在三角形內。如左圖中P的位置，如果往四方移動，半徑肯定會擴大，所以這種情況可以直接解方程組。如果是鈍角三角形，如右圖，外心在P處，BC的中垂線上到BC兩點距離相等，PQ之間都可以把A包進去。要找一個半徑最小的圓。當然是以 Q為圓心QB為半徑的圓啦。具體實現見程式碼。









 AC程式碼：


#include<iostream>
#include<cstring>
#include<cmath>
#include<string>
#include<cstdio>
using namespace std;

int main()
{
    int tes;
    int cas=0;
    double x1,y1,x2,y2,x3,y3,a,b,r2,x,y;
    scanf("%d",&tes);
    while(tes--)
    {
        scanf("%lf%lf%lf%lf%lf%lf%lf%lf",&x1,&y1,&x2,&y2,&x3,&y3,&x,&y);
        //先求出這三個點的外接圓(x-a)^2+(y-b)^2=r^2;
        //r2代表r的平方

        //先判斷銳角鈍角三角形

        if((x2-x1)*(x3-x1)+(y2-y1)*(y3-y1)<0) //(x1,y1)為鈍角
        {
            a=(x3+x2)/2.0,b=(y3+y2)/2.0;
            r2=(a-x2)*(a-x2)+(b-y2)*(b-y2);
        }
        else if((x1-x2)*(x3-x2)+(y1-y2)*(y3-y2)<0) //(x2,y2)為鈍角
        {
            a=(x3+x1)/2.0,b=(y3+y1)/2.0;
            r2=(a-x1)*(a-x1)+(b-y1)*(b-y1);
        }
        else if((x1-x3)*(x2-x3)+(y1-y3)*(y2-y3)<0)  //(x3,y3)為鈍角
        {
            a=(x2+x1)/2.0,b=(y2+y1)/2.0;
            r2=(a-x1)*(a-x1)+(b-y1)*(b-y1);
        }
        else
        {
            a=((x1*x1+y1*y1-x2*x2-y2*y2)*(y1-y3)-(x1*x1+y1*y1-x3*x3-y3*y3)*(y1-y2))/(2.0*((y1-y3)*(x1-x2)-(y1-y2)*(x1-x3)));
            b=((x1*x1+y1*y1-x2*x2-y2*y2)*(x1-x3)-(x1*x1+y1*y1-x3*x3-y3*y3)*(x1-x2))/(2.0*((x1-x3)*(y1-y2)-(x1-x2)*(y1-y3)));
            r2=(x1-a)*(x1-a)+(y1-b)*(y1-b);
        }
        if((x-a)*(x-a)+(y-b)*(y-b)<=r2)
            printf("Case #%d: Danger\n",++cas);
        else
            printf("Case #%d: Safe\n",++cas);
    }
    return 0;
}







            




相關文章