1 網路流相關概念
網路流的概念分為網路和流。
網路是指一種特殊的有向圖 \(G=(V,E)\),有容量和源匯點 \(s,t\)。
對於一個網路,流需要滿足以下性質:
- 每條邊上的流量不能大於它的容量。
- 每個點流入的流量等於流出的流量。
而對於整個網路和它上面的流,定義流的流量為源點流出的流量之和。根據第二條性質,它也等於匯點流入的流量。
網路流有很多問題和模型,下面詳細講解。
2 最大流
2.1 問題概述
對於一個網路,找到一個流,使得流的流量最大。
通常情況下,我們使用 Dinic 演算法求解最大流。在此之前需要先了解 FF 增廣。
2.2 FF 演算法
即 Ford-Fulkerson 演算法,是一種計算最大流的演算法的總稱,基於貪心思想。
首先我們對於一個網路 \(G\) 和一個流 \(f\) 給出如下定義:
- 對於一條邊 \((u,v)\),我們將其容量與流量之差成為剩餘容量。
- 將 \(G\) 中所有剩餘容量大於 \(0\) 的邊和節點構成的子圖稱為殘量網路,記作 \(G_f\)。
我們將 \(G_f\) 上一條從源點到匯點的路徑稱作增廣路,對於任意一條增廣路,我們給每一條邊都加上一個相等的流量,讓整個網路的流量增加,這一過程叫做增廣。
顯然,我們可以將求解最大流的過程看做不斷增廣。因此 FF 的本質就是不斷找增廣路進行增廣,直到找不到為止。
此時考慮這樣的情況:
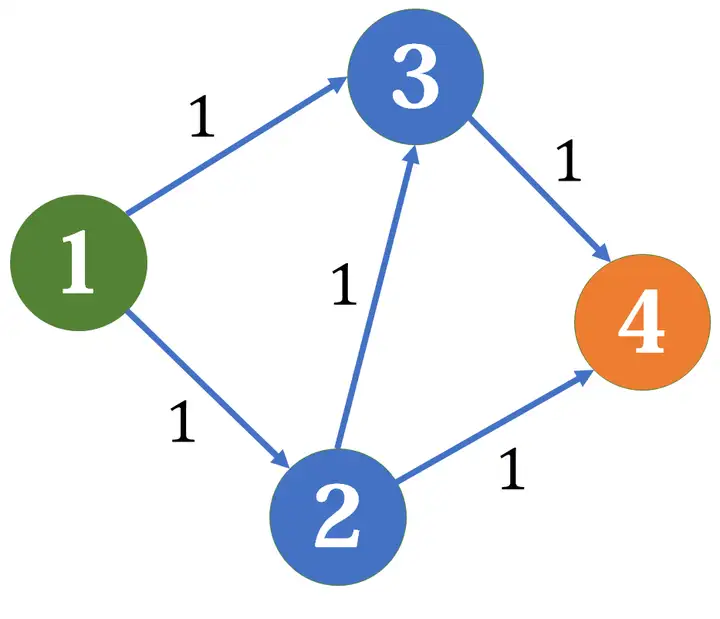
假如我們此時找到的增廣路為 \(1\to 2\to 3\to 4\),那麼殘量網路就會變成這樣:
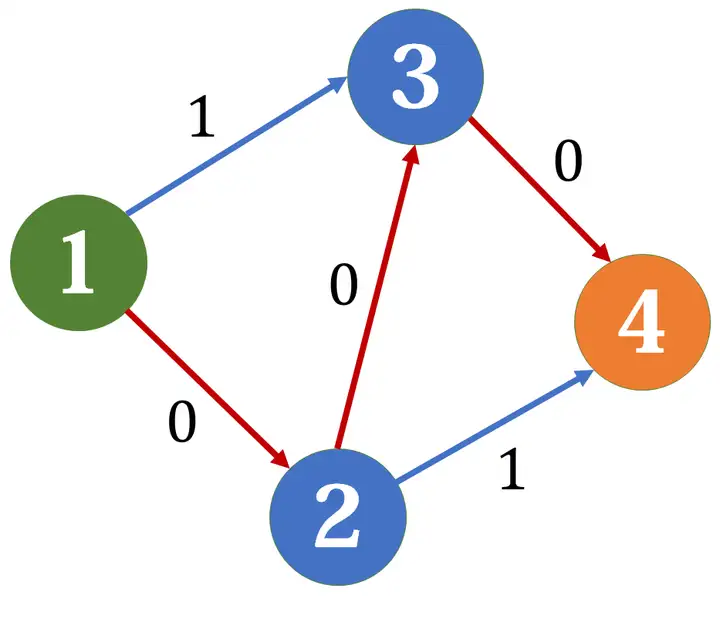
此時已經不存在增廣路了,然而最大流是 \(1\) 嗎?其實不然,顯然走 \(1\to 3\to 4,1\to 2\to 4\) 最大,流量為 \(2\)。
為了解決這樣的問題,我們引入反向邊。我們約定 \(f(u,v)=-f(v,u)\),即反向邊的流量是正向邊流量的相反數。為了保證這個性質,我們在增加 \(f(u,v)\) 值的時候,也要將 \(f(v,u)\) 減少。
可能我們會覺得負數的流量很詭異,不過我們的重點並不在於流量本身,而是殘量網路。當正向邊流量增加時,剩餘容量減少;同時反向邊流量減少,剩餘容量增加。
例如下圖:
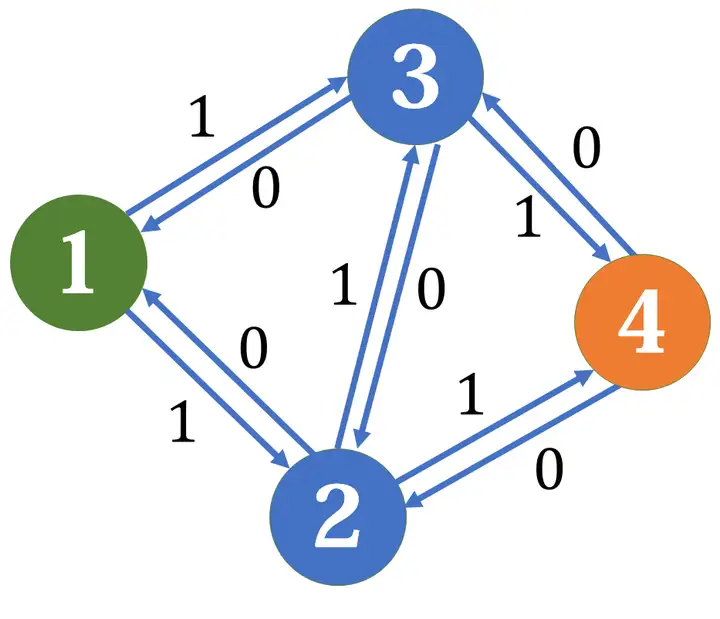
我們在反方向建邊權為 \(0\) 的邊,此時我們再次找到 \(1\to2\to3\to4\) 這條增廣路,正向的殘量網路容量應該減一,而反向的殘量網路容量要加一,如下圖:
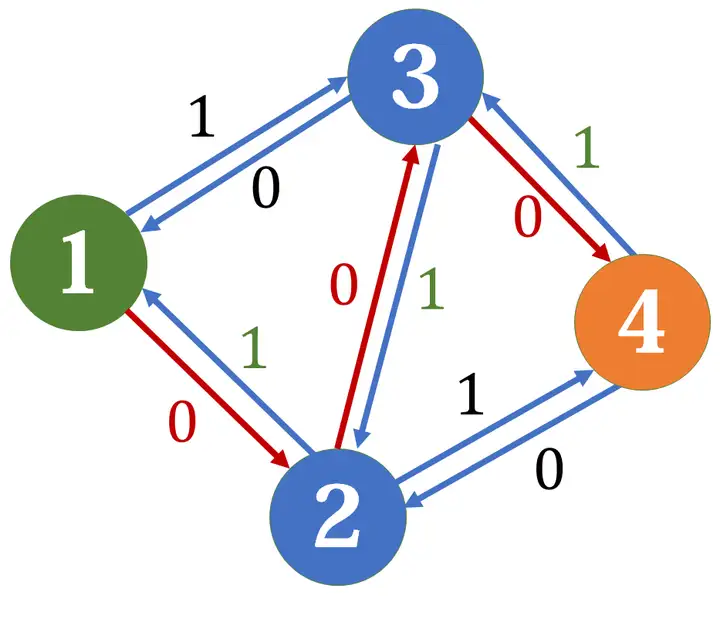
這時,我們還可以再找到一條增廣路,即 \(1\to3\to2\to4\)。
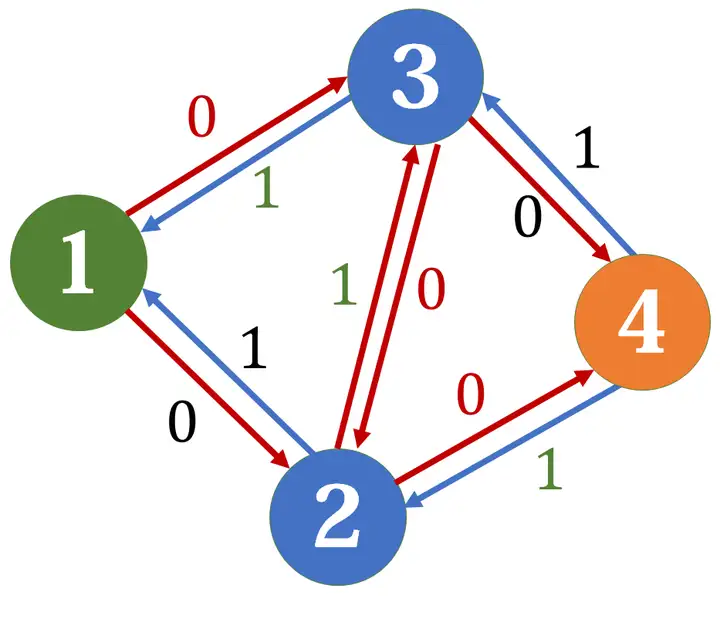
此時我們發現,\(2\to3\) 和 \(3\to2\) 我們都走了,可以認為是這條邊上的正向邊與反向邊互相抵消了,這樣我們實際得出的路徑就正好是 \(1\to2\to4,1\to3\to4\) 兩條。
因此反向邊的實質就是一種撤銷,由於反向邊時刻在加上正向邊丟失的容量,它就代表著可以撤回的容量。
這就是 FF 演算法的核心思想:殘量網路和反向邊。
接下來考慮如何實現這個演算法,顯然暴力 DFS 可行,但是時間複雜度過高,必須改進最佳化。
2.3 EK 演算法
即 Edmonds-Karp 演算法,利用 BFS 進行 FF 增廣。
EK 演算法的具體流程如下:
- 在 \(G_f\) 上如果可以從 \(s\) 出發走到 \(t\),代表我們找到了增廣路。
- 在增廣路上,求出剩餘容量的最小值,給每條邊的流量加上它,同時給反向邊容量減去它。
- 我們重複上述過程,直到沒有增廣路為止。
這就是 EK 演算法。單輪 BFS 增廣複雜度為 \(O(E)\),而增廣輪數上界為 \(O(VE)\),那麼 EK 演算法的總時間複雜度就是 \(O(VE^2)\)。當然這個複雜度是理論上界。
然而 FF 增廣和 EK 演算法都不是求最大流的主流演算法,真正最有用的是下面這個。
2.4 Dinic 演算法
Dinic 演算法是對於 FF/EK 演算法的最佳化,將兩者使用的 DFS 和 BFS 相結合。
我們在增廣前對 \(G_f\) 進行 BFS 分層,也就是根據節點 \(u\) 到源點 \(s\) 的距離 \(d(u)\) 將節點分為若干層。我們讓每個節點 \(u\) 都只向自己的下一層的節點 \(v\) 進行增廣,這樣我們每次增廣的都是原圖中邊數最少的路徑。
接下來我們進行 DFS,每次尋找到一條增廣路並更新到答案中,直到找不到增廣路後回溯。
有了這樣的指導,我們可以寫出一個最最樸素(可以說是錯誤)的 Dinic 出來:
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int Maxn = 2e5 + 5;
const int Inf = 2e9;
int n, m, s, t;
int head[Maxn], edgenum = 1;//和 tarjan 求橋很像,利用 edgenum=1 判斷雙向邊
struct node {
int nxt, to, w;
}edge[Maxn];
void add(int from, int to, int w) {//加邊要加雙向邊
edge[++edgenum] = {head[from], to, w};
head[from] = edgenum;
edge[++edgenum] = {head[to], from, 0};
head[to] = edgenum;
}
int dis[Maxn];
bool bfs() {
for(int i = 1; i <= n; i++) dis[i] = 0;
queue <int> q;
q.push(s);
dis[s] = 1;
while(!q.empty()) {
int x = q.front();
q.pop();
for(int i = head[x]; i; i = edge[i].nxt) {
int to = edge[i].to, w = edge[i].w;
if(w > 0 && dis[to] == 0) {//找到還未遍歷且還有剩餘容量的
dis[to] = dis[x] + 1;//預處理距離
if(to == t) return 1;//找到一條 s->t 的路徑
q.push(to);
}
}
}
return 0;//不存在增廣路了
}
int dfs(int x, int flow) {//上一層傳入的流量
if(x == t) return flow;//找到匯點就返回
int rest = flow;//殘量網路
for(int i = head[x]; i; i = edge[i].nxt) {
int to = edge[i].to, w = edge[i].w;
if(w > 0 && dis[to] == dis[x] + 1) {//還有剩餘容量且在下一層
int k = dfs(to, min(rest, w));//計算下面的層能經過的流量,也就是當前點能經過的流量
rest -= k;//剩餘容量減少
edge[i].w -= k;
edge[i ^ 1].w += k;//反向剩餘容量增加
}
}
return flow - rest;//返回當前節點能經過的流量
}
int ans = 0;
void dinic() {
while(bfs()) {//重複找有無增廣路,建立分層圖
ans += dfs(s, Inf);//從源點出發找
}
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> m >> s >> t;
for(int i = 1; i <= m; i++) {
int u, v, w;
cin >> u >> v >> w;
add(u, v, w);
}
dinic();
cout << ans << '\n';
return 0;
}
我們發現,此時的 Dinic 使用的 DFS 本質上還是一個暴力,複雜度也並不優秀,因此我們在上面說這是一個錯誤的 Dinic。實際上,它並不完整,我們還需要一個東西:當前弧最佳化。
觀察程式碼,我們發現如果有一個節點 \(u\),入邊和出邊都很多,那麼每一次 \(u\) 接受來自入邊的流量都要遍歷出邊決定將流量傳遞給誰,這樣會使得時間複雜度驟增。我們考慮這樣一種現象:如果對於一條邊 \((u,v)\),它已經被增廣到了極限(邊 \((u,v)\) 沒有剩餘容量或 \(v\) 後側已經不可能再被增廣),此時再走 \((u,v)\) 就變得毫無意義。
放到 Dinic 中來看,我們對於一個節點下一層的節點,一定會把這個節點之後的邊的剩餘容量榨乾,此時我們就不需要再走這個節點了。因此對於每個節點 \(u\),維護在它的出邊中第一條還需要嘗試的邊,程式碼中體現為原本的 head[x] 換成這個指標 cur[x]。
於是我們就可以保證 Dinic 的正確時間複雜度。對於單次 DFS,我們可以找到不超過 \(E\) 條的最短路徑,每一條最短路徑回溯不超過 \(V\) 次,同時當前弧最佳化保證不會經過相同節點。最佳化後每一次遍歷的最短路徑長度都會至少加一,因此至多尋找 \(V\) 次,所以複雜度為 \(O(V^2E)\)。
但是仔細思考會發現,如果一個圖要滿足上面提到的所有 “不超過” 條件來卡滿複雜度是比較困難的。實際運用中,很少會有人專門卡 Dinic,因此這個複雜度僅僅是一個理論上限,大部分圖中,Dinic 的表現都十分優秀。
當然 Dinic 還有一些別的常數最佳化,如下:
- 剩餘流量判斷:如果上一層節點傳遞的流量已經消耗完了,就不用再進行 DFS。
- 多路增廣:如果我們找到了一條增廣路,那麼我們不用回到 \(s\) 重新遍歷,如果還剩下多餘的容量沒有用,我們繼續再該點嘗試找到更多增廣路。其實這一最佳化在 DFS 中是完全自然而看起來非常簡單的,但是它確實是一種常數最佳化。
所以最終版本的 Dinic 程式碼如下:
#include <bits/stdc++.h>
#define int long long
using namespace std;
typedef long long LL;
const int Maxn = 2e5 + 5;
const int Inf = 2e9;
int n, m, s, t;
int head[Maxn], edgenum = 1;//和 tarjan 求橋很像,利用 edgenum=1 判斷雙向邊
struct node {
int nxt, to, w;
}edge[Maxn];
int cur[Maxn];//當前弧
void add(int from, int to, int w) {//加邊要加雙向邊
edge[++edgenum] = {head[from], to, w};
head[from] = edgenum;
edge[++edgenum] = {head[to], from, 0};
head[to] = edgenum;
}
int dis[Maxn];
bool bfs() {
for(int i = 1; i <= n; i++) {
dis[i] = 0;
cur[i] = head[i];//當前弧最佳化的初始化
}
queue <int> q;
q.push(s);
dis[s] = 1;
while(!q.empty()) {
int x = q.front();
q.pop();
for(int i = head[x]; i; i = edge[i].nxt) {
int to = edge[i].to, w = edge[i].w;
if(w > 0 && dis[to] == 0) {//找到還未遍歷且還有剩餘容量的
dis[to] = dis[x] + 1;//預處理距離
if(to == t) return 1;//找到一條 s->t 的路徑
q.push(to);
}
}
}
return 0;//不存在增廣路了
}
int dfs(int x, int flow) {//上一層傳入的流量
if(x == t) return flow;//找到匯點就返回
int rest = flow;//殘量網路
for(int i = cur[x]; i && rest/*剩餘容量判斷*/; i = edge[i].nxt) {
cur[x] = i;//當前弧最佳化
int to = edge[i].to, w = edge[i].w;
if(w > 0 && dis[to] == dis[x] + 1) {//還有剩餘容量且在下一層
int k = dfs(to, min(rest, w));//找到下面的層能經過的流量
rest -= k;//剩餘容量減少
edge[i].w -= k;
edge[i ^ 1].w += k;//反向剩餘容量增加
}
}
return flow - rest;//返回當前節點能經過的流量
}
int ans = 0;
void dinic() {
while(bfs()) {//重複找有無增廣路,建立分層圖
ans += dfs(s, Inf);//從源點出發找
}
}
signed main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> m >> s >> t;
for(int i = 1; i <= m; i++) {
int u, v, w;
cin >> u >> v >> w;
add(u, v, w);
}
dinic();
cout << ans << '\n';
return 0;
}