點分治
樹的重心(前置芝士)
如果在樹中選擇某個節點並刪除,這棵樹將分為若干棵子樹,統計子樹節點數並記錄最大值。取遍樹上所有節點,使此最大值取到最小的節點被稱為整個樹的重心。
性質
- 樹的重心如果不唯一,則至多兩個且相鄰
- 以樹的重心為根時,所有子樹的大小都不超過整棵樹大小的一半
- 樹中所有點到某個點的距離和中,到重心的距離和是最小的;如果有兩個重心,那麼到它們的距離和一樣
- 把兩棵樹透過一條邊相連得到一棵新的樹,那麼新的樹的重心在連線原來兩棵樹的重心的路徑上
- 在一棵樹上新增或刪除一個葉子,那麼它的重心最多隻移動一條邊的距離
如何求重心
在 DFS 中計算每個子樹的大小,記錄「向下」的子樹的最大大小,利用總點數 - 當前子樹(這裡的子樹指有根樹的子樹)的大小得到「向上」的子樹的大小,然後就可以依據定義找到重心了
int head[N], e[N], ne[N]; // head儲存邊的起點編號,e儲存邊的終點編號,ne儲存所有終點
int siz[N], // siz[x]表示以x為根的子樹大小
mx[N], // mx[x]表示選擇x為根,其所有子樹大小的最大值
rt; // 樹的重心
int vis[N];
void getCentroid(int u, int fa){
siz[u] = 1, mx[u] = 0;
for(int i = head[u]; i; i = ne[i]){
if(e[i] != fa && !vis[x]){ // vis下面會講
getCentroid(e[i], u);
siz[u] += siz[e[i]];
mx[x] = max(mx[x], siz[e[i]]);
}
}
mx[x] = max(mx[x], n - siz[x]);
if(mx[x] < mx[rt]) rt = x;
}
點分治(正式)
點分治是一種解決樹上問題的常用方法,本質思想是選擇一點作為分治中心,將原問題劃分為幾個相同的子樹上的問題遞迴解決
常見題目中給出的都是無根樹(維護的資訊與根節點無關)
我們選擇樹的重心作為根節點,其性質2保證了遞迴層數最少,是\(O(logn)\)的
細節
注意到,每一次遞迴下去時,選擇的根節點總是當前子樹的重心,但是新的根不一定是之前的根的兒子,如下圖
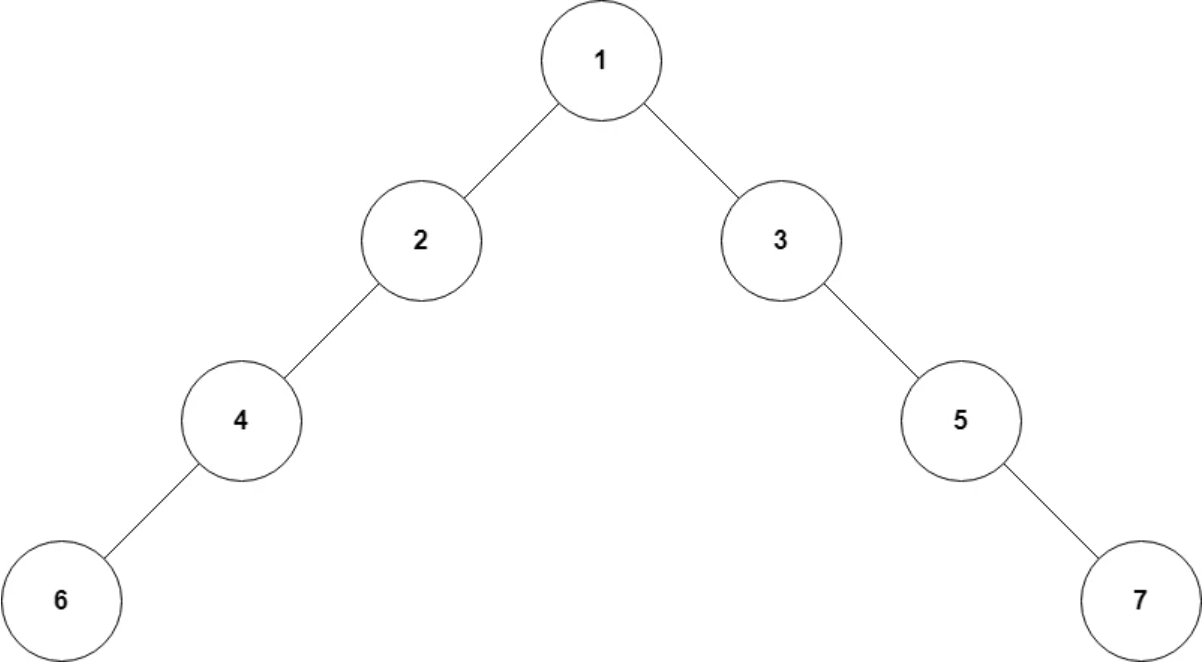
第一次找到的根為 \(1\),遞迴下去後兩顆子樹上的重心分別為 \(4\) 和 \(5\),都不是 \(1\) 的兒子,所以為了防止重複遞迴,應當每個節點進行點分治後加上標記,之後的遞迴不再進入已經打過標記的點,這也就是上面函式中 vis[] 的作用。
例題
P3806 【模板】點分治 1
思路
離線處理
對於一條長度為 \(k\) 的路徑,分為經過 \(rt\) 和不經過 \(rt\) 兩種情況,不經過的情況可以遞迴進入子樹處理
對於經過 \(rt\) 的路徑,列舉所有子節點 \(ch\) ,以 \(ch\) 為根計算 \(ch\) 子樹中所有節點到 \(rt\) 的距離。
假設子樹中出現了距離 \(rt\) 為 \(l\) 的鏈,如果 \(k-l\) 在其他的子樹中出現,那麼 \(k\) 就會出現。注意到兩者出現順序無影響,所以可以依次遞迴子樹
- \(DFS\) 處理當前子樹每個點與 \(rt\) 的距離
- 在 \(DFS\) 過程中同時統計有哪些長度出現
- 與之前子樹中出現的長度結合更新答案
- 將當前子樹的資訊併入
最後要清空記錄的之前子樹出現的長度,不能使用memset,要使用佇列保證時間複雜度正確
AC程式碼
#include <iostream>
#include <queue>
using namespace std;
const int INF = 2e9;
const int N = 1e4 + 10;
int n, m, a, b, v, k, Q[N];
int head[N], e[N << 1], w[N << 1], ne[N << 1], idx; // w 表示邊權
int siz[N], mx[N], sum, rt;
int dist[N], dd[N], cnt; // dist[x]儲存 x 到 rt 的距離, dd[x] 記錄當前子樹擁有的鏈的長度, cnt 記錄當前子樹到 rt 的鏈的個數
bool tf[10000010], vis[N], ans[N]; // tf[x]儲存是否有長度為 x 的鏈
queue<int> tag;
void add(int a, int b, int v) {
e[++idx] = b, w[idx] = v, ne[idx] = head[a], head[a] = idx;
}
void calcsiz(int x, int fa) {
siz[x] = 1, mx[x] = 0; //初始化
for (int i = head[x]; i; i = ne[i]) {
if (e[i] == fa || vis[e[i]]) continue;
calcsiz(e[i], x);
siz[x] += siz[e[i]];
mx[x] = max(mx[x], siz[e[i]]);
}
mx[x] = max(mx[x], sum - siz[x]);
if (mx[x] < mx[rt]) rt = x;
}
void calcdist(int x, int fa){
dd[++cnt] = dist[x];
for(int i = head[x]; i; i = ne[i])
if(e[i] != fa && !vis[e[i]]) dist[e[i]] = dist[x] + w[i], calcdist(e[i], x);
}
void dfz(int x, int fa){
tf[0] = true, tag.push(0), vis[x] = true;
// 列舉所有子節點
for(int i = head[x]; i; i = ne[i]){
if(e[i] == fa || vis[e[i]]) continue;
dist[e[i]] = w[i], calcdist(e[i], x);
// 與之前子樹中出現的長度結合更新答案
for(int i = 1; i <= cnt; i++)
for(int j = 1; j <= m; j++)
if(Q[j] >= dd[i]) ans[j] |= tf[Q[j] - dd[i]]; // 看有沒有 k-l 的邊
// 將當前子樹資訊併入
for(int i = 1; i <= cnt; i++)
// 觀察題目資料範圍詢問不會超過1e7
if(dd[i] < 1e7 + 10) tag.push(dd[i]), tf[dd[i]] = true;
cnt = 0;
}
// 至此,經過 rt 的情況被解決,清空佇列
while(!tag.empty()) tf[tag.front()] = false, tag.pop();
// 遞迴進入子樹
for(int i = head[x]; i; i = ne[i]){
if(e[i] == fa || vis[e[i]]) continue;
rt = 0;
mx[rt] = INF, sum = siz[e[i]];
calcsiz(e[i], x), calcsiz(rt, -1), dfz(rt, x);
}
}
int main() {
cin >> n >> m;
for (int i = 1; i < n; i++) {
cin >> a >> b >> v;
add(a, b, v), add(b, a, v);
}
for(int i = 1; i <= m; i++) cin >> Q[i];
rt = 0;
mx[rt] = INF, sum = n;
calcsiz(1, -1), calcsiz(rt, -1), dfz(rt, -1);
for(int i = 1; i <= m; i++){
if(ans[i]) cout << "AYE\n";
else cout << "NAY\n";
}
return 0;
}
Tips
程式碼中呼叫兩次 calcsiz 是因為,從上一層分治中傳下來的子樹大小在這一層是不適用的,雖然這麼求解也是對的,但是不推薦這麼做
證明
參考連結:OI Wiki,部落格園